江西省抚州市南城县2022年九年级中考模拟数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、﹣5 C、5 D、2. 下列图形中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图所示的几何体,其左视图是( )
3. 如图所示的几何体,其左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4.
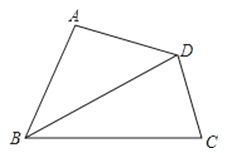
4.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
 A、7.5 B、8 C、15 D、无法确定5. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
A、7.5 B、8 C、15 D、无法确定5. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )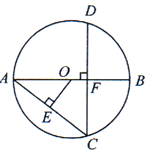 A、9.6 B、4 C、5 D、106. 如图,在平面直角坐标系中,平行于x轴的直线 ,与二次函数 , 分别交于A、B和C、D,若 ,则a为( )
A、9.6 B、4 C、5 D、106. 如图,在平面直角坐标系中,平行于x轴的直线 ,与二次函数 , 分别交于A、B和C、D,若 ,则a为( )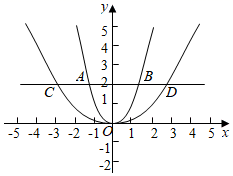 A、4 B、 C、2 D、
A、4 B、 C、2 D、二、填空题
-
7. 因式分解: .8. 第七次全国人口普查数据显示,江西省常住人口约为4518.86万人,将4518.86万用科学记数法表示 .9. 开学前,根据学校防疫要求,小芸同学连续14天进行了体温测量,结果统计如下表:
体温( )
36.3
36.4
36.5
36.6
36.7
36.8
天数(天)
2
3
3
4
1
1
这14天中,小芸体温的众数是 .
10. 不等式组的解集是 .11. 设 是关于x的方程 的两个根,且 ,则 .12. 已知 的半径为 , 是 的弦,点 在 上, .若点 到直线 的距离为 ,则 的度数为 .三、解答题
-
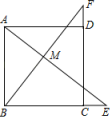
13.(1)、计算:(2)、如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连接AE和BF相交于点M.求证:AE=BF.
 14. 先化简,再求值: , 然后选一个你喜欢的x值代入求值.15. “菊润初经雨,橙香独占秋”,如图,橙子是一种甘甜爽口的水果,富含丰维生C.某水果商城为了了解两种橙子市场销售情况,购进了一批数量相等的“血橙”和“脐橙”供客户对比品尝,其中购买“脐橙”用了420元,购买“血橙”用了756元,已知每千克“血橙”进价比每千克“脐橙”贵8元.求每千克“血橙”和“脐橙”进价各是多少元?
14. 先化简,再求值: , 然后选一个你喜欢的x值代入求值.15. “菊润初经雨,橙香独占秋”,如图,橙子是一种甘甜爽口的水果,富含丰维生C.某水果商城为了了解两种橙子市场销售情况,购进了一批数量相等的“血橙”和“脐橙”供客户对比品尝,其中购买“脐橙”用了420元,购买“血橙”用了756元,已知每千克“血橙”进价比每千克“脐橙”贵8元.求每千克“血橙”和“脐橙”进价各是多少元? 16. 已知和都是等边三角形,点B,C,E,F在同一直线上,请仅用无刻度直尺画图:
16. 已知和都是等边三角形,点B,C,E,F在同一直线上,请仅用无刻度直尺画图:
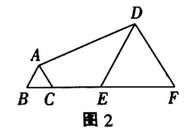 (1)、在图1中,点C与点E重合,画出线段的中点P;(2)、在图2中,点E是线段的中点,画一条与相等的线段.17. 如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
(1)、在图1中,点C与点E重合,画出线段的中点P;(2)、在图2中,点E是线段的中点,画一条与相等的线段.17. 如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .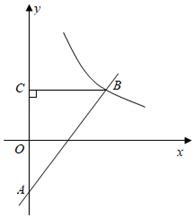 (1)、求反比例函数的解析式;(2)、求 的面积.18. 体育组为了了解九年级675名学生一分钟跳绳的情况,随机抽查了九年级部分学生进行跳绳测试(单位:个),根据测试结果
(1)、求反比例函数的解析式;(2)、求 的面积.18. 体育组为了了解九年级675名学生一分钟跳绳的情况,随机抽查了九年级部分学生进行跳绳测试(单位:个),根据测试结果组别
个数段
频数
频率
1
0≤x<80
5
0.1
2
80≤x<140
21
0.42
3
140≤x<170
a
4
170≤x<200
b
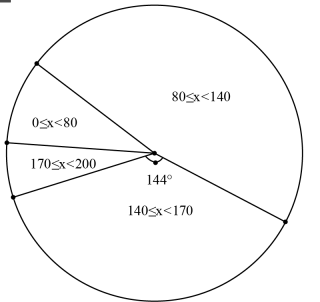 (1)、表中的数a= , b=;(2)、估算该九年级一分钟跳绳测试结果不小于140的人数;(3)、一分钟跳绳测试结果小于80的为不达标,若九年某班不达标的3人中有2个男生,1个女生、现从这3人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率19. 如图,在Rt△ABC中,∠ACB=90°.线段EF是由线段AB平移得到的,点F在边BC上,△EFD是以EF为斜边的等腰直角三角形,且点D恰好在AC的延长线上.
(1)、表中的数a= , b=;(2)、估算该九年级一分钟跳绳测试结果不小于140的人数;(3)、一分钟跳绳测试结果小于80的为不达标,若九年某班不达标的3人中有2个男生,1个女生、现从这3人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率19. 如图,在Rt△ABC中,∠ACB=90°.线段EF是由线段AB平移得到的,点F在边BC上,△EFD是以EF为斜边的等腰直角三角形,且点D恰好在AC的延长线上. (1)、求证:∠ADE=∠DFC;(2)、求证:CD=BF.20. 如今,不少人在购买家具时追求简约大气的风格,图1所示的是一款非常畅销的简约落地收纳镜,其支架的形状固定不变,镜面可随意调节,图2所示的是其侧面示意图,其中OD为镜面,EF为放置物品的收纳架,AB,AC为等长的支架,BC为水平地面,已知OA=BD=40cm,OD=120cm, . (结果精确到1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,≈1.41,≈1.73)
(1)、求证:∠ADE=∠DFC;(2)、求证:CD=BF.20. 如今,不少人在购买家具时追求简约大气的风格,图1所示的是一款非常畅销的简约落地收纳镜,其支架的形状固定不变,镜面可随意调节,图2所示的是其侧面示意图,其中OD为镜面,EF为放置物品的收纳架,AB,AC为等长的支架,BC为水平地面,已知OA=BD=40cm,OD=120cm, . (结果精确到1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,≈1.41,≈1.73)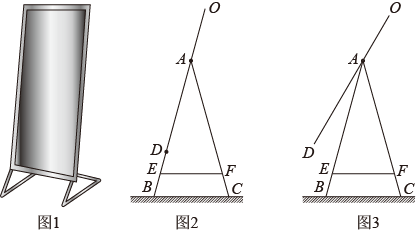 (1)、求支架顶点A到地面BC的距离;(2)、如图3,将镜面顺时针旋转15°,求此时收纳镜顶部端点O到地面BC的距离.21. 如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且 .
(1)、求支架顶点A到地面BC的距离;(2)、如图3,将镜面顺时针旋转15°,求此时收纳镜顶部端点O到地面BC的距离.21. 如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且 .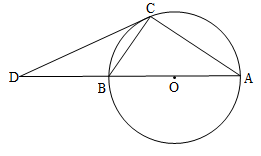 (1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为 , 的面积为 , 求CD的长.22. 定义:从三角形(不是等腰三角形)的一个顶点引出一条射线与对边相交,顶点与交点所连线段把这个三角形分割成两个小三角形,如果其中一个为等腰三角形,另一个与原三角形相似,我么就把这条线段叫做这个三角形的“华丽分割线”.
(1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为 , 的面积为 , 求CD的长.22. 定义:从三角形(不是等腰三角形)的一个顶点引出一条射线与对边相交,顶点与交点所连线段把这个三角形分割成两个小三角形,如果其中一个为等腰三角形,另一个与原三角形相似,我么就把这条线段叫做这个三角形的“华丽分割线”.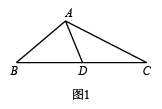
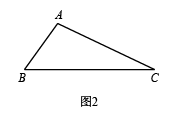
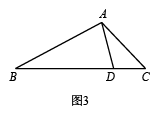
例如:如图1,AD把△ABC分成△ABD和△ADC,若△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的“华丽分割线”.
(1)、【定义感知】如图1,在中, , AB=BD.求证:AD是的“华丽分割线”.
(2)、【问题解决】①如图2,在中, , AD是的“华丽分割线”,且是等腰三角形,则的度数是 ▲ ;
②如图3,在中,AB=2,AC= , AD是 的“华丽分割线”,且是以AD为底边的等腰三角形,求华丽分割线AD的长.
23. 如图,在平面直角坐标系中,抛物线与x轴交于点A、B,与y轴交于点C,连接BC, , 对称轴为直线 , 点D为此抛物线的顶点.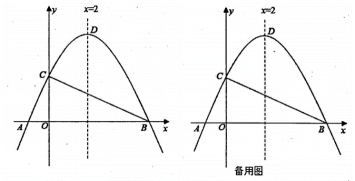 (1)、求抛物线的解析式;(2)、点E是第一象限内抛物线上的动点,连接BE和CE,求面积的最大值;(3)、点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
(1)、求抛物线的解析式;(2)、点E是第一象限内抛物线上的动点,连接BE和CE,求面积的最大值;(3)、点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.