黑龙江省绥化市2022年九年级中考二模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法表示为（）

A、 $675 \times 1 0^{2}$ 吨 B、 $67.5 × 1 0^{3}$ 吨 C、 $6.75 \times 1 0^{4}$ 吨 D、 $0.675 \times 1 0^{5}$ 吨

查看试题解析
3. 下列四个式子中，x的取值范围为x≥2的是（　　）

A、 $\frac{\sqrt{x - 2}}{x - 2}$ B、 $\frac{1}{\sqrt{x - 2}}$ C、 $\sqrt{x - 2}$ D、 $\sqrt{2 - x}$

查看试题解析
4.
在市委、市府的领导下，全市人民齐心协力，将我市成功地创建为“全国文明城市”，为此小红特制了一个正方体玩具，其展开图如图所示，原正方体中与“全”字所在的面相对的字应是（　　）

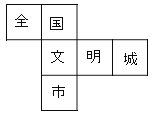A、文 B、明 C、城 D、市

查看试题解析
5. 下列运算正确的是（）

A、 $3 a + 2 a = 5 a^{2}$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 $\sqrt{a^{2}} = a$ D、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$

查看试题解析
6. 下列四个命题中，属于真命题的是（）

A、若 $\sqrt{a^{2}} = m$ ，则 $a = m$ B、若 $a > b$ ，则 $a m > b m$ C、两个等腰三角形必定全等 D、位似图形一定是相似图形

查看试题解析
7. 不能作为正多边形的内角的度数的是（）

A、120° B、108° C、144° D、145°

查看试题解析
8. 设 $α$ ， $β$ 是一元二次方程 $x^{2} + 2 x - 1 = 0$ 的两个根，则 $α^{2} + β^{2}$ 的值是（）

A、－2 B、2 C、4 D、6

查看试题解析
9. 下列说法正确的是（）

A、为了了解全国中学生的心理健康情况，应采用全面调查的方式 B、一组数据5，6，7，6，6，8，10的众数和中位数都是6 C、一个游戏的中奖概率是0.1，则做10次这样的游戏一定会中奖 D、若甲组数据的方差S_甲²=0.05，乙组数据的方差S_乙²=0.1，则乙组数据比甲组数据稳定

查看试题解析
10. 某电子元件厂准备生产4600个电子元件，甲车间独立生产了一半后，由于要尽快投入市场，乙车间也加入该电子元件的生产，若乙车间每天生产的电子元件是甲车间的1.3倍，结果用33天完成任务，问甲车间每天生产电子元件多少个？在这个问题中设甲车间每天生产电子元件x个，根据题意可得方程为（）

A、 $\frac{2300}{x} + \frac{2300}{1 . 3x} = 33$ B、 $\frac{2300}{x} + \frac{2300}{x + 1 . 3x} = 33$ C、 $\frac{2300}{x} + \frac{4600}{x + 1 . 3x} = 33$ D、 $\frac{4600}{x} + \frac{2300}{x + 1 . 3x} = 33$

查看试题解析
11. 如图，在矩形ABCD中，AB＝4，BC＝8，E为CD边的中点，P，Q为BC边上两个动点，且PQ＝2，当四边形APQE的周长最小时，BP的长为（）

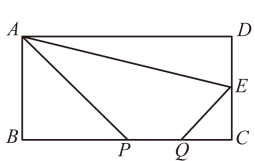A、0 B、3 C、4 D、6

查看试题解析
12. 如图，▱ABCD的对角线AC ， BD交于点O ， CE平分∠BCD交AB于点E ，交BD于点F ，且∠ABC＝60°，AB＝2BC ，连接OE.下列结论：①∠ACD＝30°；②S_▱_ABCD＝AC·BC；③OE∶AC＝ $\sqrt{3}$ ∶6；④S_△_OCF＝2S_△_OEF.成立的个数有（　　）

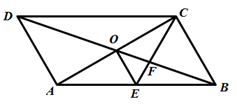A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 在－1，0， $\frac{1}{3} ， \sqrt{2}$ ， π中任取一个数，取到无理数的概率是．

查看试题解析
14. 分解因式： $x^{3} - 2 x^{2} - 3 x =$ ．

查看试题解析
15. 如果圆锥的底面周长是20π，侧面展开后所得的扇形的圆心角为120°，则圆锥的母线长是．

查看试题解析
16. 当 $x - 2 y = 0$ ，代数式 $(x - \frac{2 x y - y^{2}}{x}) \div \frac{x^{2} - y^{2}}{x}$ 的值为．

查看试题解析
17. 如图，建筑物BC上有一旗杆AB，点D到BC的距离为20m，在点D处观察旗杆顶部A的仰角为52°，观察底部B的仰角为45°，则旗杆的高度为m．（精确到0.1m，参考数据： $s i n 52 ° \approx 0.79$ ， $t a n 52 ° \approx 1.28$ ， $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ．）

查看试题解析
18. 一工地计划租用甲、乙两辆车清理淤泥，从运输量来估算：若单独租用甲车，15天可以完成任务；若单独租用乙车，30天可以完成任务．已知两车合运，共需租金65000元，甲车每天的租金比乙车每天的租金多1500元．在租甲、乙两车，单独租甲车，单独租乙车这三种方案中，租金最少是元．

查看试题解析
19. 如图，正方形 $A B C D$ 和正三角形 $A E F$ 都内接于 $⊙ O$ ， $E F$ 与 $B C$ ， $C D$ 分别相交于点 $G$ ， $H$ ，则 $\frac{E F}{G H}$ 的值是．

查看试题解析
20. 如图，正方形ABCD的顶点C，D均在双曲线 $y = \frac{10}{x}$ 在第一象限的分支上，顶点A，B分别在x轴、y轴上，则此正方形的边长为．

查看试题解析
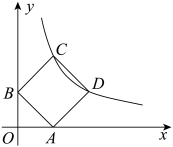21. 如图，在矩形ABCD中，AB＝4，BC＝3，点P、Q分别为直线AB、BC上的动点，且PD⊥PQ，当△PDQ为等腰三角形时，则AP的长为．

查看试题解析
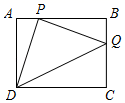22. 用同样大小的黑色棋子按如图所示的规律摆放，则第2022个图形中有颗黑色棋子．

查看试题解析

三、解答题

23. 如图，在△ABC中，AB＝AC＝6，∠ABC＝72°．

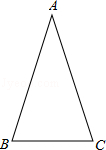(1)、用直尺和圆规作出一条射线BM交AC于点M，把△ABC分成等腰三角形ABM和等腰三角形BCM（保留作图痕迹，不要求写作法）；

(2)、求BC边的长．

查看试题解析
24. 如图，在 $11 \times 11$ 的正方形网格中，每个小正方形的边长都为1，网格中有一个格点三角形ABC（即三角形的顶点都在格点上）．

(1)、在图中作出△ABC关于直线l对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、作出△ABC绕点C顺时针旋转90°后得到的 $△ A_{2} B_{2} C$ ；

(3)、在（2）的案件下，求点B旋转到点 $B_{2}$ 所经过的路径长．

查看试题解析
25. 图，AB是 $⊙ O$ 的弦，D为半径OA的中点，过点D作 $C D ⊥ O A$ 交弦AB于点E，交 $⊙ O$ 于点F，且CE＝CB，连接AF，BF．

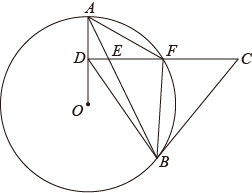(1)、求证：BC是 $⊙ O$ 的切线；

(2)、求∠ABF的度数；

(3)、如果BE＝4， $s i n ∠ O A B = \frac{1}{2}$ ，求 $⊙ O$ 的半径．

查看试题解析
26. 甲、乙两车分别从M，N．两地沿同一公路相向匀速行驶，两车分别抵达N，M两地后即停止行驶．已知乙车比甲车提前出发，设甲、乙两车之间的路程为s（单位：km），乙车行驶的时间为t（单位：h），s与t的函数关系如图所示．

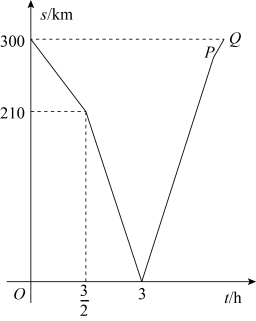(1)、M，N两地之间的公路路程是km，乙车的速度是km/h；

(2)、当乙车抵达M地时．甲车离N地还有多少千米？

(3)、求线段PQ的解析式．

查看试题解析
27. 在菱形ABCD中，∠BAD=60°．

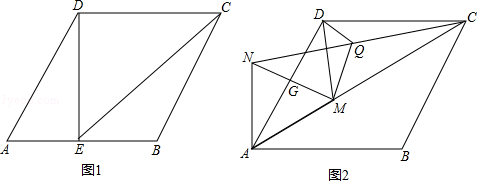(1)、如图1，点E为线段AB的中点，连接DE，CE，若AB=4，求线段EC的长；

(2)、如图2，M为线段AC上一点（M不与A，C重合），以AM为边，构造如图所示等边三角形AMN，线段MN与AD交于点G，连接NC，DM，Q为线段NC的中点，连接DQ，MQ，求证：DM=2DQ．

查看试题解析
28. 图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于点A和点 $B (1 ， 0)$ ，与y轴交于点 $C (0 ， 3)$ ，其对称轴为 $x = - 1$ ．

(1)、求抛物线的解析式，并写出其顶点坐标；

(2)、若动点P在第二象限内的抛物线上，动点N在对称轴上．
①当PA⊥NA，且PA＝NA时，求此时点P的坐标；
②求四边形PABC面积的最大值及此时点P的坐标．

查看试题解析