黑龙江省齐齐哈尔市铁锋区2022年九年级下学期一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 早在两千多年前,中国人就已经开始使用负数,并运用到生产和生活中,比西方早一千多年,下列各式计算结果为负数的是( )A、 B、 C、 D、2. 下列计算正确的是( ).A、 B、 C、 D、3. 现实世界中,对称现象无处不在,中国的方块字中有些也只有对称性,下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则所需的小正方体的个数最多是( )
4. 如图,由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则所需的小正方体的个数最多是( )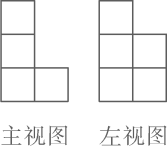 A、 B、 C、 D、5. 一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )A、 B、 C、 D、6. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、
A、 B、 C、 D、5. 一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )A、 B、 C、 D、6. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、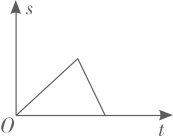 B、
B、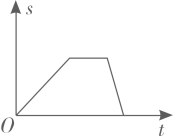 C、
C、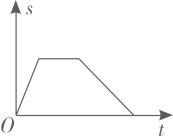 D、
D、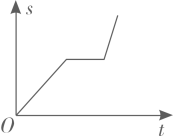 7. 已知关于x的分式方程 =1的解是负数,则m的取值范围是( )A、m≤3 B、m≤3且m≠2 C、m<3 D、m<3且m≠28. 在抗击疫情知识竞赛中,为奖励成绩突出的学生,学校计划用200元钱购买A、B、C三种奖品,A种每个10元,B种每个20元,C种每个30元,在种奖品不超过两个且钱全部用尽的情况下,有多少种购买方案( )A、7种 B、8种 C、14种 D、15种9. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )
7. 已知关于x的分式方程 =1的解是负数,则m的取值范围是( )A、m≤3 B、m≤3且m≠2 C、m<3 D、m<3且m≠28. 在抗击疫情知识竞赛中,为奖励成绩突出的学生,学校计划用200元钱购买A、B、C三种奖品,A种每个10元,B种每个20元,C种每个30元,在种奖品不超过两个且钱全部用尽的情况下,有多少种购买方案( )A、7种 B、8种 C、14种 D、15种9. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )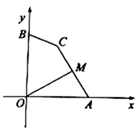 A、 B、 C、 D、10. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )
A、 B、 C、 D、10. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )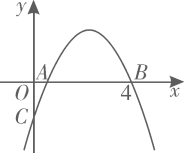 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
11. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒,数3000000用科学记数法表示为.12. 如图, 和 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使 和 全等.
 13. 小明在手工制作课上,用面积为 ,半径为 的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 .14. 若关于的不等式只有2个正整数解,则的取值范围为 .15. 在平面直角坐标系xOy中,点A,B在反比例函数y=(x>0)的图象上,且点A与点B关于直线y=x对称,C为AB的中点,若AB=4,则线段OC的长为 .
13. 小明在手工制作课上,用面积为 ,半径为 的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 .14. 若关于的不等式只有2个正整数解,则的取值范围为 .15. 在平面直角坐标系xOy中,点A,B在反比例函数y=(x>0)的图象上,且点A与点B关于直线y=x对称,C为AB的中点,若AB=4,则线段OC的长为 .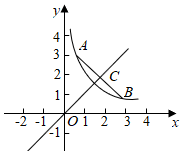 16. 在矩形 中, , ,点E在边 上,且 ,连接 ,将 沿 折叠.若点B的对应点 落在矩形 的边上,则折痕的长为 .17. 如图,已知直线: , 直线:和点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , …,按此作法进行下去,则点的横坐标为 .
16. 在矩形 中, , ,点E在边 上,且 ,连接 ,将 沿 折叠.若点B的对应点 落在矩形 的边上,则折痕的长为 .17. 如图,已知直线: , 直线:和点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , …,按此作法进行下去,则点的横坐标为 .
三、解答题
-
18.(1)、计算:(2)、因式分解:19. 解方程: .20. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
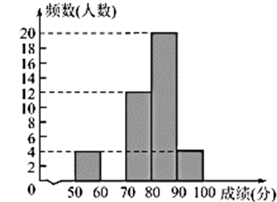
信息二:第三组的成绩(单位:分)为74 71 73 74 79 76 77 76 76 73 72 75
根据信息解答下列问题:
(1)、补全第二组频数分布直方图(直接在图中补全);(2)、第三组竞赛成绩的众数是分,抽取的50名学生竞赛成绩的中位数是分;(3)、若该校共有1500名学生参赛,请估计该校参赛学生成绩不低于80分的约为人.21. 如图,在 中, ,点O在 上,以 为半径的半圆O交 于点D,交 于点E,过点D作半圆O的切线 ,交 于点F. (1)、求证: ;(2)、若 , , ,求半圆O的半径长.22. , 两城市之间有一条公路相连,公路中途穿过市,甲车从市到市,乙车从市到市,两车在途中匀速行驶,甲车的速度比乙车的速度慢20千米/时,两车距离市的路程(单位:千米)与甲车行驶的时间(单位:小时)的函数图象如图所示,结合图象信息,解答下列问题:
(1)、求证: ;(2)、若 , , ,求半圆O的半径长.22. , 两城市之间有一条公路相连,公路中途穿过市,甲车从市到市,乙车从市到市,两车在途中匀速行驶,甲车的速度比乙车的速度慢20千米/时,两车距离市的路程(单位:千米)与甲车行驶的时间(单位:小时)的函数图象如图所示,结合图象信息,解答下列问题: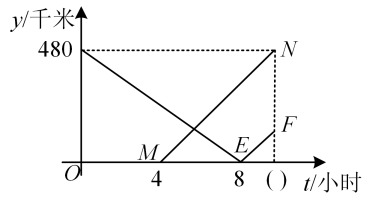 (1)、图中括号内应填入的数为 , 、两市相距的路程为千米;(2)、求图象中线段所在直线的函数解析式,不需要写出自变量的取值范围;(3)、直接写出甲车出发后几小时,两车距市的路程之和是300千米.23. 综合与实践
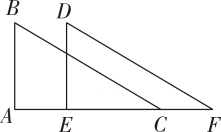
(1)、图中括号内应填入的数为 , 、两市相距的路程为千米;(2)、求图象中线段所在直线的函数解析式,不需要写出自变量的取值范围;(3)、直接写出甲车出发后几小时,两车距市的路程之和是300千米.23. 综合与实践综合与实践上,老师组织同学们以“正方形的旋转”为主题开展数学活动,“智慧小组”选行了下面的探究:已知正方形与正方形 , 正方形保持不变,正方形绕点旋转一周.
 (1)、操作发现:
(1)、操作发现:当点在正方形的边上时,如图①所示,连接、 , 若 , , 则的值为;
(2)、探究证明:当正方形旋转至图②的位置时,连接、 , 试写出与的数量关系,并加以证明;
(3)、拓展延伸:连接、 , 分别取、的中点、 , 连接 , , 当正方形绕点旋转一周时,请直接写出线段所扫过的面积.
24. 综合与探究已知抛物线与轴交于、两点(点在点的左边),与轴交于点 , 顶点的坐标为 .
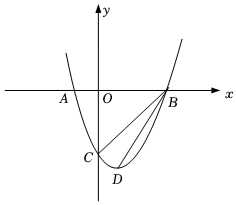 (1)、求抛物线的解析式.(2)、求的值.(3)、若直线将四边形的面积分为两部分,则的值为 .(4)、点是轴上的动点,点是抛物线上的动点,是否存在点、 , 使得以点、、、为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式.(2)、求的值.(3)、若直线将四边形的面积分为两部分,则的值为 .(4)、点是轴上的动点,点是抛物线上的动点,是否存在点、 , 使得以点、、、为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.