黑龙江省齐齐哈尔市龙江县三校联考2022年九年级第二次升学模拟数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列各数中,化简结果为﹣2022的是( )A、﹣(﹣2022) B、 C、|﹣2022| D、2. 利用图形旋转可以设计一些美丽的图案,下列图案,可以由一个“基本图形”连续旋转45°得到的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的有( )个
3. 下列计算正确的有( )个①±=±4② ×= 1 ③(﹣2a2)3=﹣8a3 ④= 1
A、1 B、2 C、3 D、44. 2022北京冬奥会期间,为了表达对志愿者工作的支持,某班学生积极参加捐款活动,该班50名学生的捐款统计情况如表:金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的众数与中位数是( )
A、20 ,10 B、17,14 C、10,20 D、17,205. 将一副三角板如图所示的位置放在直尺上,则∠1的度数是( )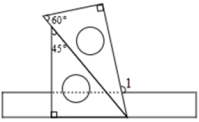 A、115° B、105° C、110° D、95°6. 由若干个完全相同的小立方块搭成的几何体的左视图和俯视图如图所示,则搭成该几何体所用的小立方块的个数可能是( )
A、115° B、105° C、110° D、95°6. 由若干个完全相同的小立方块搭成的几何体的左视图和俯视图如图所示,则搭成该几何体所用的小立方块的个数可能是( )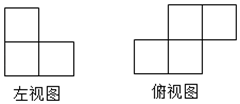 A、4个 B、6个 C、7个 D、8个7. 如图所示的电路中,随机闭合开关S1 , S2 , S3中的两个,则能让两盏灯泡同时发光的概率为( )
A、4个 B、6个 C、7个 D、8个7. 如图所示的电路中,随机闭合开关S1 , S2 , S3中的两个,则能让两盏灯泡同时发光的概率为( )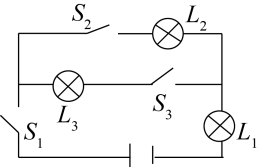 A、 B、 C、 D、8. 新冠状病毒传染性非常强,多是通过飞沫,接触,还有气溶胶传播。所以一定要做好个人防护,尽量少外出,更不要聚集,佩戴医用外科口罩是非常有效的个人防护。为了个人防护,小红用40元钱买了A,B两种型号的医用外科口罩(两种型号都买),A型每包6元,B型每包4元,在40元全部用尽的情况下,有几种购买方案( )A、2种 B、3种 C、4种 D、5种9. 如图,矩形ABCD中,AB=4,BC=6,点P从B点出发,沿B→C→D方向移动,连接DP,过P作PQ⊥DP交边AB于点Q,设点P走的路程为x,线段BQ的长度为y,则y与x之间函数图象大致为( )
A、 B、 C、 D、8. 新冠状病毒传染性非常强,多是通过飞沫,接触,还有气溶胶传播。所以一定要做好个人防护,尽量少外出,更不要聚集,佩戴医用外科口罩是非常有效的个人防护。为了个人防护,小红用40元钱买了A,B两种型号的医用外科口罩(两种型号都买),A型每包6元,B型每包4元,在40元全部用尽的情况下,有几种购买方案( )A、2种 B、3种 C、4种 D、5种9. 如图,矩形ABCD中,AB=4,BC=6,点P从B点出发,沿B→C→D方向移动,连接DP,过P作PQ⊥DP交边AB于点Q,设点P走的路程为x,线段BQ的长度为y,则y与x之间函数图象大致为( )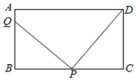 A、
A、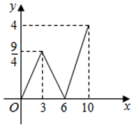 B、
B、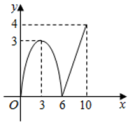 C、
C、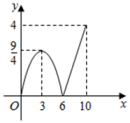 D、
D、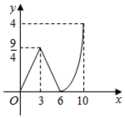 10. 如图,抛物线y=ax2+bx+c的对称轴为 , 经过点(﹣2,0),下列结论:①a=b;②abc<0;③;④点A(x1 , y1),B(x2 , y2)在抛物线y=ax2+bx+c上,当时,y1<y2;⑤若ax12+bx1=ax22+bx2且x1≠x2 , 则x1+x2=﹣1.其中正确结论的个数有( )
10. 如图,抛物线y=ax2+bx+c的对称轴为 , 经过点(﹣2,0),下列结论:①a=b;②abc<0;③;④点A(x1 , y1),B(x2 , y2)在抛物线y=ax2+bx+c上,当时,y1<y2;⑤若ax12+bx1=ax22+bx2且x1≠x2 , 则x1+x2=﹣1.其中正确结论的个数有( )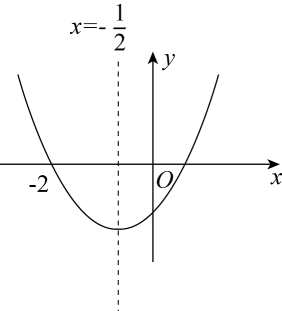 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
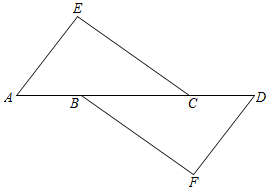
11. 2021年5月15日,我国“天问一号”探测器在火星成功着陆.火星具有和地球相近的环境,与地球最近时候的距离约55000000km.将数字55000000用科学记数法表示为.12. 如图,AE//DF,.添加下列条件中的一个:①;②;③;④EC//BF.其中能证明≌的是 (只填序号).
 13. 在综合与实践活动课上,某同学需要用扇形薄纸板制作成底面半径为3分米,高为4分米的圆锥形生日帽,如图所示,则该扇形薄纸板的圆心角为 度
13. 在综合与实践活动课上,某同学需要用扇形薄纸板制作成底面半径为3分米,高为4分米的圆锥形生日帽,如图所示,则该扇形薄纸板的圆心角为 度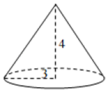 14. 已知一个三角形三边的长分别为5、7、a,且关于y的分式方程=2的解是非负数,则符合条件的整数a的值为。15. 如图,点B是反比例函数图象上的一点,矩形OABC的周长是12,正方形BCFG和正方形OCDE的面积之和为30,则反比例函数的解析式为
14. 已知一个三角形三边的长分别为5、7、a,且关于y的分式方程=2的解是非负数,则符合条件的整数a的值为。15. 如图,点B是反比例函数图象上的一点,矩形OABC的周长是12,正方形BCFG和正方形OCDE的面积之和为30,则反比例函数的解析式为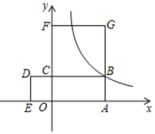 16. 已知AD是△ABC的中线,E是AD的三等分点,连接BE并延长交AC于F.则AF : FC为.17. 在直角坐标系中,等边△AOB如图放置,点A的坐标为(1,0),每一次将△AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A1OB1;第二次旋转后得到△A2OB2 , …,以此类推,则点A2022的坐标为 .
16. 已知AD是△ABC的中线,E是AD的三等分点,连接BE并延长交AC于F.则AF : FC为.17. 在直角坐标系中,等边△AOB如图放置,点A的坐标为(1,0),每一次将△AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A1OB1;第二次旋转后得到△A2OB2 , …,以此类推,则点A2022的坐标为 .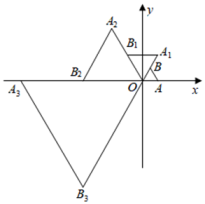
三、解答题
-
18.(1)、计算:(2)、因式分解: .19. 解方程:(x﹣1)(x﹣2)=1220. 推广普及国家通用语言文字是新时代语言文字工作的首要任务,某校举行“汉字听写”比赛,每位学生听写汉字39个,赛后随机抽查部分学生的成绩,以下是根据抽查结果绘制的统计图的一部分.
组别
正确个数x
组中值
A
0≤x<8
4
B
8≤x<16
12
C
16≤x<24
20
D
24≤x<32
28
E
32≤x<40
36
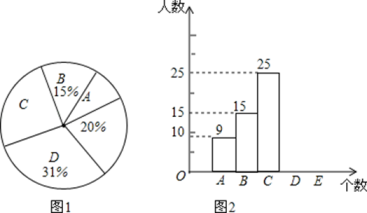
根据以上信息解决下列问题:
(1)、本次调查的样本容量为 ▲ , 并补全条形统计图;(2)、在扇形统计图中C组对应的扇形圆心角是;(3)、若每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写符合题意个数的平均数为 . (一个组的组中值指这个组两个端点数值的平均数)(4)、该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请估计这所学校本次比赛听写不合格的学生人数.21. 如图, 内接于 , ,点E在直径CD的延长线上,且 .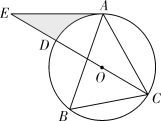 (1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.22. 如图1所示,在A,B两地之间有汽车站C站,客车由C站驶往A地,到达A地后立即原速驶往B地,货车由B地驶往A地,两车同时出发,匀速行驶.图2是客车、货车离C站的距离y(千米)与行驶时间x(小时)之间的函数关系图象,请结合图象信息解答下列问题:
(1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.22. 如图1所示,在A,B两地之间有汽车站C站,客车由C站驶往A地,到达A地后立即原速驶往B地,货车由B地驶往A地,两车同时出发,匀速行驶.图2是客车、货车离C站的距离y(千米)与行驶时间x(小时)之间的函数关系图象,请结合图象信息解答下列问题: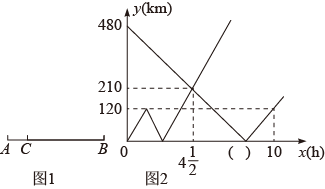 (1)、A,B两地间的距离是千米;客车速度为(km/h) ;(2)、请直接在图2中的括号内填上符合题意数字;(3)、求货车由B地驶往A地过程中,y与x之间的函数关系式,并写出自变量x的取值范围;(4)、直接写出客、货两车出发多长时间,距各自出发地的距离相等。23. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)、A,B两地间的距离是千米;客车速度为(km/h) ;(2)、请直接在图2中的括号内填上符合题意数字;(3)、求货车由B地驶往A地过程中,y与x之间的函数关系式,并写出自变量x的取值范围;(4)、直接写出客、货两车出发多长时间,距各自出发地的距离相等。23. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.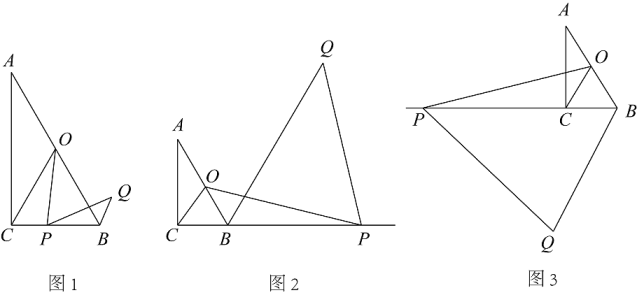 (1)、如图1,当点P在线段BC上时,连结OQ,则△OPQ是三角形;△COP≌△;线段BQ与CP的数量关系为;∠PBQ的度数
(1)、如图1,当点P在线段BC上时,连结OQ,则△OPQ是三角形;△COP≌△;线段BQ与CP的数量关系为;∠PBQ的度数为请直接写出)
(2)、当点P在CB延长线上时(如图2)和BC延长线上时(如图3),(1)中的线段BQ与CP的数量关系是否成立?若成立,请加以证明;若不成立,请说明理由;(图2、图3选择一种情况写出证明过程即可)(3)、如图2,若∠BPO=15°,则BQ与BP的数量关系为;(4)、如图3,若∠BPO=15°,AB= , 则PQ的长为24. 如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B.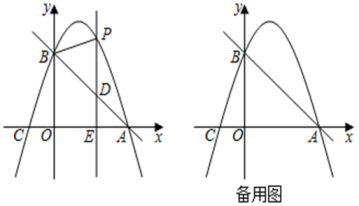 (1)、求抛物线解析式;(2)、E(m,0)是线段OA上一动点,过点E作ED⊥x轴于点E,交AB于点D,交抛物线于点P,连接PB.
(1)、求抛物线解析式;(2)、E(m,0)是线段OA上一动点,过点E作ED⊥x轴于点E,交AB于点D,交抛物线于点P,连接PB.①点E在线段OA上运动时,若△PBD是直角三角形,点P的坐标为 ▲ ;(直接写出)
②点E在线段OA上运动时,连结PC交AB于点Q,当 的值最大时,请你求出点E的坐标和的最大值.
(3)、若点H是抛物线的顶点,在x轴上有一点M,平面内是否存在点N,使得以A、H、M、N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由