黑龙江省牡丹江市2022年九年级中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、填空题
-
1. 2021年5月15日我国天问一号探测器在火星预选着陆区着陆,在火星上首次留下中国印迹,迈出我国星际探测征程的重要一步.目前探测器距离地球约320000000千米,320000000这个数据用科学记数法可表示为.2. 函数y= 中,自变量x的取值范围是 .3. 已知⊙中,直径 , 弦的长为 , 则弦所对圆周角的度数为 .4. 二次函数关于x轴对称的函数图象的解析式为 .5. 若关于x的分式方程 的解为正数,则m的取值范围是 .6. 如图,在中, , 将沿着折叠,得到 , 点M、N分别在、边上,且 . 连接 , 若 , 则 .
 7. 如图,下列每个三角形中的4个数之间都有相同的规律,根据这种规律,第n个三角形中间的数字用含n的代数式表示为 .
7. 如图,下列每个三角形中的4个数之间都有相同的规律,根据这种规律,第n个三角形中间的数字用含n的代数式表示为 . 8. 如图,正方形的边长为2,点E在边上运动(不与点A、B重合), , 点F在射线上,且 , 与相交于点G,连接 . 则下列结论:①;②;③;④面积的最大值为;⑤的周长为 , 其中正确结论的序号为 .
8. 如图,正方形的边长为2,点E在边上运动(不与点A、B重合), , 点F在射线上,且 , 与相交于点G,连接 . 则下列结论:①;②;③;④面积的最大值为;⑤的周长为 , 其中正确结论的序号为 .
二、单选题
-
9. 下列计算正确的是( )A、 B、 C、 D、10. 下列美术字中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 11. 几何体由若干个大小相同的小立方块搭成,如图是它的主视图和俯视图,则组成该几何体的小立方块的个数至少是( )
11. 几何体由若干个大小相同的小立方块搭成,如图是它的主视图和俯视图,则组成该几何体的小立方块的个数至少是( ) A、8 B、7 C、6 D、512. 如图,将圆锥沿一条母线剪开并展平,得到一个扇形,若圆锥的底面圆的半径 , 扇形的圆心角 , 则该圆锥母线的长为( )
A、8 B、7 C、6 D、512. 如图,将圆锥沿一条母线剪开并展平,得到一个扇形,若圆锥的底面圆的半径 , 扇形的圆心角 , 则该圆锥母线的长为( ) A、8 B、6 C、4 D、313. 如图,直线与x轴相交于点A,与双曲线交于点B,点C在双曲线上,若点 , 则的面积为( )
A、8 B、6 C、4 D、313. 如图,直线与x轴相交于点A,与双曲线交于点B,点C在双曲线上,若点 , 则的面积为( ) A、6 B、7 C、8 D、914. 已知一组数据:58,53,55,52,54,51,55,这组数据的中位数和众数分别是( )A、54,55 B、54,54 C、55,54 D、52,5515. 如图,在平面直角坐标系中,点A的坐标是 , 点B的坐标为 , 点C的坐标为 , 将向左平移个单位长度后,再绕点O旋转,当垂直于x轴时,点B的对应点的坐标为( )
A、6 B、7 C、8 D、914. 已知一组数据:58,53,55,52,54,51,55,这组数据的中位数和众数分别是( )A、54,55 B、54,54 C、55,54 D、52,5515. 如图,在平面直角坐标系中,点A的坐标是 , 点B的坐标为 , 点C的坐标为 , 将向左平移个单位长度后,再绕点O旋转,当垂直于x轴时,点B的对应点的坐标为( ) A、或 B、或 C、或 D、或16. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2、3,4,若随机摸出一个小球后放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、17. 若等腰三角形的周长是80cm,则能反映这个等腰三角形的腰长y(cm)与底边长x(cm)的函数关系的图像是( )A、
A、或 B、或 C、或 D、或16. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2、3,4,若随机摸出一个小球后放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、17. 若等腰三角形的周长是80cm,则能反映这个等腰三角形的腰长y(cm)与底边长x(cm)的函数关系的图像是( )A、 B、
B、 C、
C、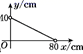 D、
D、 18. 某种商品每件的进价为120元,商场按进价提高标价,为增加销量,准备打折销售,但要保证利润率不低于 , 则至多可以打( )折A、7 B、7.5 C、8 D、8.519. 如图,在中, , 平分 , 平分 , 相交于点F,且 , , 则的长为( )
18. 某种商品每件的进价为120元,商场按进价提高标价,为增加销量,准备打折销售,但要保证利润率不低于 , 则至多可以打( )折A、7 B、7.5 C、8 D、8.519. 如图,在中, , 平分 , 平分 , 相交于点F,且 , , 则的长为( ) A、 B、 C、 D、20. 如图,抛物线 , 其顶点坐标为 , 抛物线与x轴的一个交点为 , 直线与抛物线交与A、B两点,下列结论:①;②;③方程有两个不相等的实数根:①抛物线与x轴的另一个交点是;⑤当时,有 , 其中结论正确的个数有( )
A、 B、 C、 D、20. 如图,抛物线 , 其顶点坐标为 , 抛物线与x轴的一个交点为 , 直线与抛物线交与A、B两点,下列结论:①;②;③方程有两个不相等的实数根:①抛物线与x轴的另一个交点是;⑤当时,有 , 其中结论正确的个数有( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个三、解答题
-
21. 先化简,再求值: , 其中 .22. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,抛物线经过A、B两点,且与x轴的负半轴交于点C.
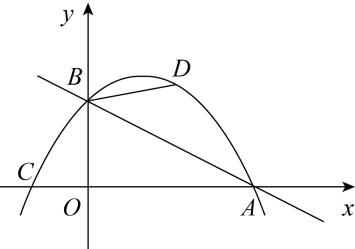 (1)、求该抛物线的解析式;(2)、若点D为直线上方抛物线上的一点, , 直接写出点D的坐标.23. 已知,以为底边的等腰三角形的外心是O,且 , 求的面积.画出正确的图形,并直接写出面积即可.24. 为进一步了解中考生对中考体育项目的选择情况,某中学对已开设的A(游泳)、B(立定跳远)、C(跑步)、D(跳绳)四种项目的学生选择情况进行调查,随机抽取了部分学生,每个学生必须选择且只选择一个项目,并将调查结果绘制成如图所示的统计图,请结合图中的信息解答下列问题:
(1)、求该抛物线的解析式;(2)、若点D为直线上方抛物线上的一点, , 直接写出点D的坐标.23. 已知,以为底边的等腰三角形的外心是O,且 , 求的面积.画出正确的图形,并直接写出面积即可.24. 为进一步了解中考生对中考体育项目的选择情况,某中学对已开设的A(游泳)、B(立定跳远)、C(跑步)、D(跳绳)四种项目的学生选择情况进行调查,随机抽取了部分学生,每个学生必须选择且只选择一个项目,并将调查结果绘制成如图所示的统计图,请结合图中的信息解答下列问题: (1)、本次调查的学生数是名;(2)、补全条形统计图:(3)、扇形统计图中,C所在的扇形圆心角的度数为;(4)、该校中考生有1080名,请你根据以上调查结果估计该校参加中考学生中选择了“跑步”和“跳绳”的一共有多少名?25. 在一条笔直的公路上依次有A、C、B三地,甲乙两人同时出发,甲从A地匀速骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原速的倍原路返回A地,乙匀速步行从B地前往A地,甲、乙两人距各自出发地的路程y(单位:米)与时间x(单位:分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)、本次调查的学生数是名;(2)、补全条形统计图:(3)、扇形统计图中,C所在的扇形圆心角的度数为;(4)、该校中考生有1080名,请你根据以上调查结果估计该校参加中考学生中选择了“跑步”和“跳绳”的一共有多少名?25. 在一条笔直的公路上依次有A、C、B三地,甲乙两人同时出发,甲从A地匀速骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原速的倍原路返回A地,乙匀速步行从B地前往A地,甲、乙两人距各自出发地的路程y(单位:米)与时间x(单位:分钟)之间的函数关系如图所示,请结合图象解答下列问题: (1)、请写出甲从A地到B地的速度为米/分,乙的速度为米/分;(2)、求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量x的取值范围);(3)、请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.26. 如图,一个含角的纸片顶点与等边的点B重合,将该纸片绕点B旋转,使纸片角的一边交直线于点D,在另一边上截取点E,使 , 连接 .
(1)、请写出甲从A地到B地的速度为米/分,乙的速度为米/分;(2)、求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量x的取值范围);(3)、请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.26. 如图,一个含角的纸片顶点与等边的点B重合,将该纸片绕点B旋转,使纸片角的一边交直线于点D,在另一边上截取点E,使 , 连接 .

 (1)、当点D在边上时,如图①,求证:;(2)、当点D在边所在直线上,如图②、如图③时,线段之间又有怎样的数量关系?请直接写出结论.(3)、在图③中,交于点K,若 , 则 , .27. “小布丁”文具厂计划生产甲、乙两种文具共40套.已知甲种文具每套成本34元,售价39元;乙种文具每套成本42元,售价50元.文具厂预计生产两种文具的成本不高于1552元,且甲种文具的数量少于20套.(1)、该文具厂有哪几种生产方案?(2)、该文具厂怎样生产获利最大?最大利润是多少?(3)、在(1)的条件下,40套文具全部售出后,文具厂又生产6套文具捐赠给社区学校,这样文具厂仅获利润25元.请直接写出文具厂是按哪种方案生产的.28. 如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在x轴的负半轴上,点C在y轴的正半轴上,直线的解析式为 , 线段的长是一元二次方程的两个根,且 .
(1)、当点D在边上时,如图①,求证:;(2)、当点D在边所在直线上,如图②、如图③时,线段之间又有怎样的数量关系?请直接写出结论.(3)、在图③中,交于点K,若 , 则 , .27. “小布丁”文具厂计划生产甲、乙两种文具共40套.已知甲种文具每套成本34元,售价39元;乙种文具每套成本42元,售价50元.文具厂预计生产两种文具的成本不高于1552元,且甲种文具的数量少于20套.(1)、该文具厂有哪几种生产方案?(2)、该文具厂怎样生产获利最大?最大利润是多少?(3)、在(1)的条件下,40套文具全部售出后,文具厂又生产6套文具捐赠给社区学校,这样文具厂仅获利润25元.请直接写出文具厂是按哪种方案生产的.28. 如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在x轴的负半轴上,点C在y轴的正半轴上,直线的解析式为 , 线段的长是一元二次方程的两个根,且 . (1)、求点A、点B的坐标;(2)、若直线l过点A交线段于点D,且 , 求经过点D的反比例函数的解析式;(3)、平面内满足以A、C、P为顶点的三角形与相似的点P有 ▲ 个.并直接写出满足条件的第一象限内两个点P的坐标.
(1)、求点A、点B的坐标;(2)、若直线l过点A交线段于点D,且 , 求经过点D的反比例函数的解析式;(3)、平面内满足以A、C、P为顶点的三角形与相似的点P有 ▲ 个.并直接写出满足条件的第一象限内两个点P的坐标.