河北省石家庄市2022年中考一模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，将线段AB绕点A旋转，下列各点能够落到线段AB上的是（）．

A、点C B、点D C、点E D、点F

查看试题解析
2. 一个数用科学记数法表示为 $3.14 \times 1 0^{7}$ ，这个数是一个（）

A、6位数 B、7位数 C、8位数 D、9位数

查看试题解析
3. 将量角器按如图方式放置，其中角度为45°的角是（）

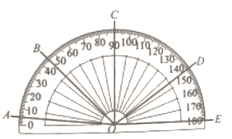A、∠AOB B、∠BOC C、∠COD D、∠DOE

查看试题解析
4. 下列计算中，得数最小的是（）

A、 $- 3 \times (\frac{1}{6} - \frac{1}{2})$ B、 $3 \times (\frac{1}{6} + \frac{1}{2})$ C、 $- 3 \times (- \frac{1}{6} + \frac{1}{2})$ D、 $3 \times (- \frac{1}{6} + \frac{1}{2})$

查看试题解析
5. 如图1是由一根细铁丝围成的正方形，其边长为1．现将该细铁丝围成一个三角形（如图2所示），则AB的长可能为（）

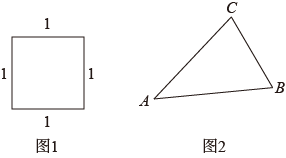A、1.5 B、2.0 C、2.5 D、3.0

查看试题解析
6. $6^{6}$ 是 $6^{3}$ 的（）

A、2倍 B、36倍 C、3倍 D、216倍

查看试题解析
7. 如图，是某位同学用带有刻度的直尺在数轴上作图的方法，若图中的虚线相互平行，则点P表示的数是（）

A、1 B、 $\sqrt{2}$ C、 $\frac{10}{3}$ D、5

查看试题解析
8. 如图有A、B、C三类卡片，分别是边长为a的正方形，边长为a，b的长方形，边长为b的正方形，若用这三种卡片拼成无缝隙不重叠的正方形，以下方案不可行的是（）

A、A类卡片1张，B类卡片2张，C类卡片1张 B、A类卡片2张，B类卡片4张，C类卡片1张 C、A类卡片1张，B类卡片4张，C类卡片4张 D、A类卡片4张，B类卡片8张，C类卡片4张

查看试题解析
9. 已知一次函数 $y = k x + b (k \neq 0)$ 满足自变量x每增加1个单位长度，函数值y就增加2个单位长度，以下选项所给的一次函数图象满足这个条件的是（）

A、 B、 C、 D、

查看试题解析
10. 如图1为一个土堆，我们可以把它的截面看成一个等腰 $△ A B C$ （如图2）．其中斜坡AB和AC与水平地面BC所成锐角为20°，最高处A距离地面0.8米，则下列说法正确的是（）

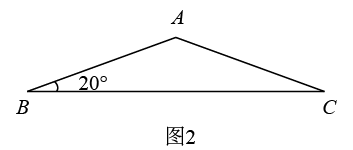A、斜坡AB的坡度是20° B、斜坡AC的坡度是 $t a n 20 °$ C、 $B C = \frac{0.8}{t a n 20 °}$ 米 D、 $A B = \frac{0.8}{c o s 20 °}$ 米

查看试题解析
11. 设 $M = \sqrt{202 1^{2} - 2020 \times 2022}$ ， $N = \sqrt{202 1^{2} - 4042 \times 2022 + 202 2^{2}}$ ，则 $M$ 与 $N$ 的关系为（）

A、 $M > N$ B、 $M < N$ C、 $M = N$ D、 $M = \pm N$

查看试题解析
12. 在 $△ A B C$ 中，D，E分别是边AB，AC的中点，按图中方法作图后，若四边形ABHG的周长与 $△ A B C$ 的周长相等， $△ A B C$ 还需具备的条件是（）

A、 $A B ⊥ B C$ B、 $A B = A C$ C、 $A C = B C$ D、 $A C = \frac{1}{2} B C$

查看试题解析
13. 有一道题：“甲队修路150m与乙队修路100m所用天数相同，若▇▇▇▇，求甲队每天修路多少米？”根据图中的解题过程，被遮住的条件是（）
解：设甲队每天修路x米，
依题意得： $\frac{150}{x} = \frac{100}{2 x - 30}$

A、甲队每天修路比乙队2倍还多30m B、甲队每天修路比乙队2倍还少30m C、乙队每天修路比甲队2倍还多30m D、乙队每天修路比甲队2倍还少30m

查看试题解析
14. 相同规格（长为14，宽为8）的长方形硬纸板，剪掉阴影部分后，将剩余的部分沿虚线折叠，制作成底面为正方形的长方体箱子，有如图所示的甲、乙两种方案，所得长方体体积分别记为： $V_{甲}$ 和 $V_{乙}$ ．下列说法正确的是：（）

A、 $V_{甲} > V_{乙}$ B、 $V_{甲} = V_{乙}$ C、 $V_{甲} < V_{乙}$ D、无法判断

查看试题解析
15. 如图，有四条直线m，n，p，q和一条曲线，曲线是反比例函数 $y = \frac{6}{x} (x > 0)$ 在平面直角坐标系中的图象，则y轴可能是（）

A、直线m B、直线n C、直线p D、直线q

查看试题解析
16. 如图，已知点P是 $⊙ O$ 上点，用直尺和圆规过点P作一条直线，使它与 $⊙ O$ 相切于点P．以下是甲、乙两人的作法：
甲：如图1，连接OP，以点P为圆心，OP长为半径画弧交 $⊙ O$ 于点A，连接并延长OA，再在OA上截取 $A B = O P$ ，直线PB即为所求；
乙：如图2，作直径PA，在 $⊙ O$ 上取一点B（异于点P，A），连接AB和BP，过点P作 $∠ B P C = ∠ A$ ，则直线PC即为所求．
对于甲、乙两人的作法，下列判断正确的是（）

A、甲、乙两人的作法都正确 B、甲、乙两人的作法都不正确 C、甲的作法正确，乙的作法不正确 D、甲的作法不正确，乙的作法符合题意

查看试题解析

二、填空题

17. 若a，b互为相反数，则 $a + b =$ ；
当 $a = 1 - \sqrt{2}$ ，则 $b =$ ．

查看试题解析
18. 如图所示，在正四边形、正五边形中，相邻两条对角线的夹角分别为 $a_{4}$ ， $a_{5}$ ，则 $a_{5}$ 为°，以此类推，正n边形相邻两条对角线的较大夹角为°．

查看试题解析
19. 抛物线 $L ： y = x^{2} + m x + n$ 经过图中的网格区域．

(1)、当抛物线L过原点及点（1，0）时， $m + n$ 的值是．

(2)、当 $m + n = 1$ ，且抛物线L恰好只经过如图网格区域（包括边界）中的3个格点（横纵坐标均为整数），则满足条件的整数m有个．

查看试题解析

三、解答题

20. 如图，数轴上从左到右有点A，B，C，D，其中点C为原点，A，D所对应的数分别为-5，1，点B为AD的中点．

(1)、在图中标出点C的位置，并直写出点B对应的数；

(2)、若在数轴上另取一点E，且B，E两点间的距离是7，求A，B，C，D，E对应的数的和．

查看试题解析
21. 其社区打算购买一批垃圾分类提示牌和垃圾箱，计划提示牌比垃圾箱多购买6个，且提示牌与垃圾箱的个数之和恰好为100个．

(1)、求计划购买提示牌多少个？

(2)、为提升居民垃圾分类意识，实际购买时增加了提示牌的购买数量，且提示牌与垃圾箱的购买数量之和不变．已知提示牌的单价为每个60元，垃圾箱的单价为每个150元，若预算费用不超过9800元，请求出实际购买提示牌的数量至少增加了多少个？

查看试题解析
22. 某学校射击队计划从甲、乙两名运动员中选取一名队员代表该校参加比赛，在选拔过程中，每名选手射击10次，根据甲、乙队员成绩绘制了如图1、图2所示的统计图：
并求得了乙队员10次射击成绩的平均数和方差：
${\bar{x}}_{乙} = 7$ 环， $S_{乙}^{2} = \frac{1}{10} [3 \times {(6 - 7)}^{2} + {(5 - 7)}^{2} + {(4 - 7)}^{2} + {(7 - 7)}^{2} + 2 \times {(9 - 7)}^{2} + {(10 - 7)}^{2} + {(8 - 7)}^{2}] = 3.4$ ．

(1)、甲队员选拔赛成绩的众数是环，乙队员选拔赛成绩的中位数是环；

(2)、求甲队员10次射击成绩的平均数和方差，根据甲、乙两名队员的选拔赛成绩，你推荐谁代表学校参加比赛，并说明理由；

(3)、为提升射击队技战术水平，学校决定除甲、乙外，再从射击队其他5名队员（三名男生，两名女生）中随机选出两名队员同前往观看比赛，请你用画树状图或列表的方法求出恰好选出一名男生和一名女生的概率．

查看试题解析
23. 如图1是一个手机支架的截面图，由底座MN、连杆 $A - B - C - D$ 和托架组成， $A B ⊥ M N$ ， BC可以绕点B自由转动，CD的长度可以进行伸缩调节，已知 $∠ B C D = 143 °$ ， $A B = 12 c m$ ， $B C = 6 c m$ ．

(1)、如图2，若AB，BC在同条直线上， $C D = 9.5 c m$ ，求点D到底座MN的距离（结果保留整数）；

(2)、如图3，调节CD长度为12cm，并转动连杆BC使 $A D ∥ B C$ 时，达到最佳视觉状态，求∠ABC的度数．（参考数据： $s i n 53 ° \approx 0.8$ ， $c o s 53 ° \approx 0.6$ ， $t a n 53 ° \approx 1.3$ ）

查看试题解析
24. 如图，在直角坐标系xOy中，直线 $l_{1} ： y = x$ 经过点 $A (4 ， a)$ ，直线 $l_{2}$ 与 $l_{1}$ 交于点 $C (1 ， b)$ ，与y轴交于点B，点A关于x轴对称的点 $A^{'}$ 在直线 $l_{2}$ 上．

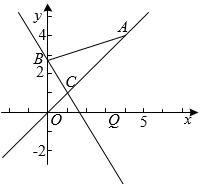(1)、求直线 $l_{2}$ 的函数表达式；

(2)、连接AB，求 $△ A O B$ 的面积；

(3)、过点 $Q (n ， 0)$ 作x轴的垂线，分别交 $l_{1}$ ， $l_{2}$ 于点M，N，若M，N两点间的距离不小于5，直接写出n的取值范围．

查看试题解析
25. 在半径为10的扇形AOB中， $∠ A O B = 90 °$ ，延长OB到点C，使 $B C = O B = 10$ ．点D为 $\overset{⌢}{A B}$ 上的动点，点E是扇形所在平面内的点，连接OD，DE，EC，当 $D E = E C = 10$ 时，解答下列问题：

(1)、论证：如图1，连接OE，DC，当 $O D ∥ E C$ 时，求证： $O E = D C$ ；

(2)、发现：当 $∠ D O C = 60 °$ 时，∠ODE的度数可能是多少？

(3)、尝试：如图2，当点D，E，C三点共线时，求点D到OA所在直线的距离；

(4)、拓展：当点E在OC的下方，且DE与 $\overset{⌢}{A B}$ 相切时，直接写出∠DOC的余弦值．

查看试题解析
26. 如图1的小山丘是科研部门的小球弹射实验场地，在小山丘一侧的山坡上建有小球弹射发射装置，另一侧建有圆柱形小球接收装置，如图2为实验场地的纵截面示意图，小山丘纵截面的外部轮廓线近似为抛物线的一部分，以小山丘纵截面与地面的交线为x轴，以过发射装置所在的直线AB为y轴，建立平面直角坐标系，发射装置底部在轮廓线的点A处，距离地面为1米，在发射装置3米的点B处是发射点，已知小山丘纵截面的外部轮廓线为 $C_{1} ： y = - \frac{1}{12} x^{2} + \frac{7}{6} x + 1$ ，从发射装置的发射点弹射一个小球（忽略空气阻力）时，小球的飞行路线为一段抛物线 $C_{2} ： y = - \frac{1}{8} x^{2} + b x + c$ ．

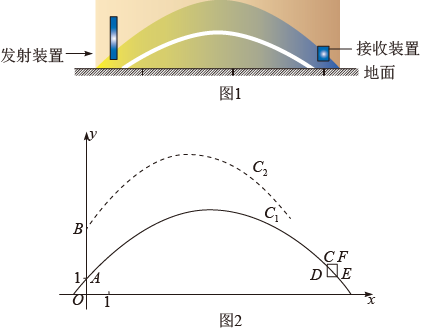(1)、直接写出c的值，当小球离B处的水平距离和竖直距离都为4米时，求b的值，并求小球到小山丘的竖直距离为1米时，小球离B处的水平距离；

(2)、若小球最远着陆点到y轴的距离为15米，当小球飞行到小山丘顶的正上方，且与顶部距离不小于 $\frac{2}{3}$ 米时，求b的取值范围，并求小球飞行路线的顶点到x轴距离的最小值；

(3)、圆柱形小球接收装置的最大截面为矩形CDEF，已知点E在 $C_{1}$ 上，其横坐标为14， $C F ∥ x$ 轴， $C D = 1.5$ ， $D E = 1$ ．若小球恰好落入该装置内（不触碰装置侧壁），请直接写出b的取值范围．

查看试题解析