河北省邯郸市2022年中考一模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图， $∠ A O B$ 的一边OB经过的点是（）

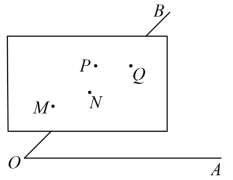A、P点 B、Q点 C、M点 D、N点

查看试题解析
2. 在计算 $- \frac{1}{3} + 1 - \frac{5}{3}$ 时通常转化成 $- \frac{1}{3} - \frac{5}{3} + 1$ ，这个变形的依据是（）

A、移项 B、加法交换律 C、加法结合律 D、乘法分配律

查看试题解析
3. 如图，在正方形ABCD中，点O是 $△ B C D$ 的内心，连接BO并延长交CD于F点，则 $∠ B F C$ 的度数是（）

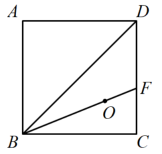A、45° B、60° C、67.5° D、75°

查看试题解析
4. “m与n差的3倍”用代数式可以表示成（）

A、 $3 m - n$ B、 $m - 3 n$ C、 $3 (n - m)$ D、 $3 (m - n)$

查看试题解析
5. 如图，已知点A与点C关于点O对称，点B与点D也关于点O对称，若 $B C = 3$ ， $O D = 4$ ．则AB的长可能是（）

A、3 B、4 C、7 D、11

查看试题解析
6. 与 $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}}$ 结果相同的是（）

A、 $1 + \frac{1}{2} - \frac{1}{3}$ B、 $1 - \frac{1}{2} + \frac{1}{3}$ C、 $1 + \frac{1}{2} + \frac{1}{3}$ D、 $1 - \frac{1}{2} - \frac{1}{3}$

查看试题解析
7. 若图1所示的正方体表面展开图是图2，则正方体上面的几何图形是（）．

A、 B、 C、 D、

查看试题解析
8. 如图，在平面直角坐标系中，一次函数 $y = - 2 x + 1$ 的图像可以是（）

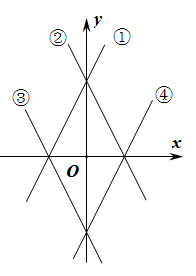A、① B、② C、③ D、④

查看试题解析
9. 如图是某晾衣架的侧面示意图，根据图中数据，则C、D两点间的距离是（）

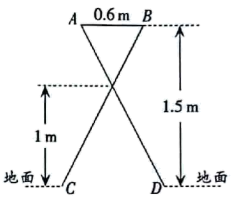A、0.9m B、1.2m C、1.5m D、2.5m

查看试题解析
10. 已知n是正整数，若 $4^{n} + 4^{n} + 4^{n} + 4^{n} = 8^{4}$ ，则n的值是（）

A、4 B、5 C、6 D、8

查看试题解析
11. 已知：如图，在平行四边形ABCD中，对角线AC平分∠BCD，求证：四边形ABCD是菱形．
证明：∵四边形ABCD是平行四边形，∴ $A D$ ．
∴ $∠ D A C = ∠ B C A$ ．
∵对角线AC平分 $∠ B C D$ ， ∴ $∠ B C A = ∠ D C A$ ．
∴ $∠ D A C = ∠ D C A$ ．
∴四边形ABCD是菱形．
为了推理更加严谨，在“∴ $∠ D A C = ∠ D C A$ ”和“∴四边形ABCD是菱形”之间的补充，下列说法正确的是（）

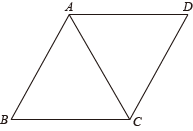A、已经严谨，不用补充 B、应补充“∴AC平分 $∠ B A D$ ” C、应补充“∴ $D A = D C$ ” D、应补充“∴ $D A = A B$ ”

查看试题解析
12. 已知a、c互为相反数，则关于x的方程 $a x^{2} + 5 x + c = 0 (a \neq 0)$ 根的情况（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、有一根为5

查看试题解析
13. 某轮滑队所有队员的年龄只有12、13、14、15、16（岁）五种情况，其中部分数据如图所示，若队员年龄的唯一的众数与中位数相等，则这个轮滑队队员人数m最小是（）

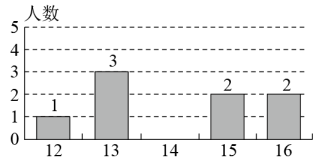A、9 B、10 C、11 D、12

查看试题解析
14. 如图1，在边长为2的正六边形ABCDEF中，M是BC的中点，连接EM交AD于N点，若 $M N = a$ ，则表示实数a的点落在数轴上（如图2）标有四段中的（）

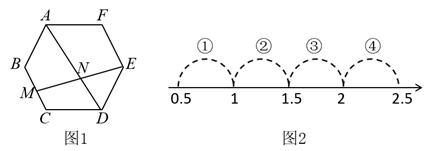A、段① B、段② C、段③ D、段④

查看试题解析

15. 在化简

\frac{2 m}{m^{2} - 4} + \frac{1}{2 - m}

时，两位同学分别给出如下方法：

佳佳的方法是：

$\begin{array}{l} \frac{2 m}{m^{2} - 4} + \frac{1}{2 - m} \\ = \frac{2 m}{m^{2} - 4} - \frac{1}{m + 2} \\ = \frac{2 m}{(m + 2) (m - 2)} - \frac{m - 2}{(m + 2) (m - 2)} \\ = \frac{2 m - m + 2}{(m + 2) (m - 2)} \\ = \frac{1}{m - 2} \end{array}$

音音的方法是：

$\begin{array}{l} \frac{2 m}{m^{2} - 4} + \frac{1}{2 - m} \\ = \frac{2 m}{(m + 2) (m - 2)} + \frac{m + 2}{(2 - m) (m + 2)} \\ = \frac{2 m}{(m + 2) (m - 2)} - \frac{m + 2}{(m - 2) (m + 2)} \\ = 2 m - m - 2 \\ = m - 2 \end{array}$

则对于两人的方法，正确的是（）

A、两人方法均正确 B、佳佳正确，音音不正确 C、佳佳不正确，音音正确 D、两人方法均不正确

查看试题解析

16. 如图，对于几何作图“过直线l外一点P作这条直线的平行线”，甲、乙两位同学均设计自己的尺规作图的方案：甲：在直线l上取点A，以点P为圆心，PA为半径画圆，交直线l于另一点B，然后作直径AC，最后作 $∠ C P B$ 的平分线PQ，PQ所在的直线即为所求；乙：在直线l上取A、B两点（B点在A点的右侧），分别以点P为圆心，AB为半径，以点B为圆心，PA为半径画弧，两弧相交于Q点（点Q和点A在直线PB的两旁），PQ所在的直线即为所求．对于以上两个方案，判断正确的是（）

A、甲、乙均正确 B、甲不正确、乙正确 C、甲正确、乙不正确 D、甲、乙均不正确

查看试题解析

二、填空题

17. $2^{- 1}$ 的倒数是， $2^{- 1}$ 的绝对值是．

查看试题解析
18. 如图，用铁丝折成一个四边形ABCD（点C在直线BD的上方），且∠A=70°，∠BCD=120°，若使∠ABC、∠ADC平分线的夹角∠E的度数为100°，可保持∠A不变，将∠BCD （填“增大”或“减小”）°．

查看试题解析
19. 如图，在平面直角坐标系中，点A(−2，3)，点B与点A关于直线x=1对称，过点B作反比例函数y= $\frac{m}{x}$ (x>0)的图像．

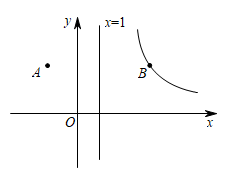(1)、m=；

(2)、若对于直线y=kx−5k+4，总有y随x的增大而增大，设直线y=kx−5k+4与双曲线y= $\frac{m}{x}$ (x>0)交点的横坐标为t，则t的取值范围是．

查看试题解析

三、解答题

20. 嘉淇在解一道数学计算题时，发现有一个数被污染了．

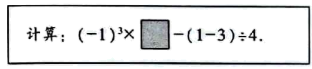(1)、嘉淇猜污染的数为1，请计算 ${(- 1)}^{3} \times 1 - (1 - 3) \div 4$ ；

(2)、老师说，嘉淇猜错了，正确的计算结果不小于 $\frac{5}{2}$ ，求被污染的数最大是几？

查看试题解析
21. 某景区有一座步行桥（如图），需要把阴影部分涂刷油漆．

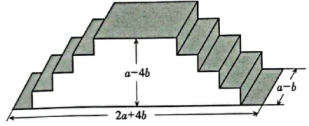(1)、求涂刷油漆的面积；

(2)、若 $a = 901$ ， $b = 1$ ，请用科学记数法表示涂刷油漆的面积．

查看试题解析
22. 如图，把一个质地均匀的转盘，分成两个扇形，其中有一个扇形的圆心角为120°，在每个扇形上标上数字．保持指针不动，转动转盘，转盘停止后，指针会指向某个扇形，并相应得到这个扇形所标的数字（若指针指向分割线，当做指向该分割线右边的扇形）．

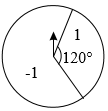(1)、转动转盘一次，求得到负数的概率；

(2)、数学王老师提出一个问题“转动转盘两次，将得到的数字相加，求和为0的概率”．嘉嘉发现这个问题有点难，便向淇淇请教，淇淇经过认真思考后，把写有“-1”的扇形，均分成两个小扇形，再求解这个问题就容易多了，请你按照淇淇的思路求解上述问题．

查看试题解析
23. 在平面直角坐标系中，抛物线 $y = a x (x - 4) (a \neq 0)$ 与x轴相交于A、B两点，且A点在B点的左侧，点C在其对称轴上，且点C的纵坐标为2．

(1)、求 $△ A B C$ 的面积；

(2)、若 $- 2 \leq x \leq 4$ 时，二次函数 $y = a x (x - 4) (a \neq 0)$ 有最小值为-4，求a的值．

查看试题解析
24. 如图，在扇形AOB中， $∠ A O B = 90 °$ ， C、D是 $\overset{⌢}{A B}$ 上两点，过点D作 $D E ∥ O C$ 交OB于E点，在OD上取点F，使 $O F = D E$ ，连接CF并延长交OB于G点．

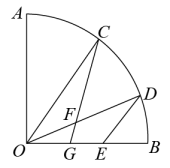(1)、求证： $△ O C F ≌ △ D O E$ ；

(2)、若C、D是AB的三等分点， $O A = 2 \sqrt{3}$ ：
①求 $∠ O G C$ ；

②请比较GE和BE的大小．

查看试题解析
25. 某小超市计划购进甲、乙两种商品共100件，其中甲商品每件的进价为20元，乙商品每件的进价由基础价与浮动价两部分组成，其中基础价固定不变，浮动价与购进乙商品件数成反比，现购进乙商品x件，乙商品每件的进价为P元．在购进过程中，可以获得如下信息：
x（件）
10
50
P（元）
70
38

(1)、求P与x之间函数关系式；

(2)、若乙商品每件的进价是甲商品的2倍，求x的值；

(3)、若购进甲商品的总钱数不超过购进乙商品的总钱数，求小超市购进这两种商品的最少花费．

查看试题解析
26. 如图1，在矩形ABCD中， $A B = 6$ ， $A D = 8$ ，把AB绕点B顺时针旋转 $α (0 < α < 180 °)$ 得到，连接，过B点作 $B E ⊥ A A^{^{'}}$ 于E点，交矩形ABCD边于F点．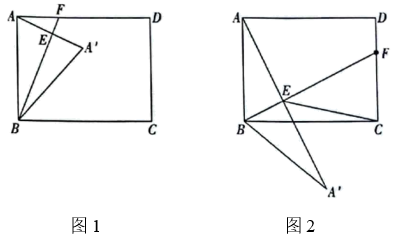

(1)、求DA′的最小值；

(2)、若A点所经过的路径长为 $2 π$ ，求点A′到直线AD的距离；

(3)、如图2，若 $C F = 4$ ，求 $t a n ∠ E C B$ 的值；

(4)、当 $∠ A' C B$ 的度数取最大值时，直接写出CF的长．

查看试题解析

x（件）	10	50
P（元）	70	38