河北省承德市2022年数学一模试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. ﹣1+3的结果是( )A、﹣4 B、4 C、﹣2 D、22. 如图,王华用橡皮泥做了个圆柱,再用手工刀切去一部分,则其左视图是( )
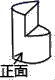 A、
A、 B、
B、 C、
C、 D、
D、 3. 2012﹣2013NBA整个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( )A、科比罚球投篮2次,一定全部命中 B、科比罚球投篮2次,不一定全部命中 C、科比罚球投篮1次,命中的可能性较大 D、科比罚球投篮1次,不命中的可能性较小4. 对于反比例函数 ,下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、图象是中心对称图形 D、当x<0时,y随x的增大而增大5. 在一次训练中,甲、乙、丙三人各射击10次的成绩(单位:环)如图,在这三人中,此次射击成绩最稳定的是( )
3. 2012﹣2013NBA整个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( )A、科比罚球投篮2次,一定全部命中 B、科比罚球投篮2次,不一定全部命中 C、科比罚球投篮1次,命中的可能性较大 D、科比罚球投篮1次,不命中的可能性较小4. 对于反比例函数 ,下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、图象是中心对称图形 D、当x<0时,y随x的增大而增大5. 在一次训练中,甲、乙、丙三人各射击10次的成绩(单位:环)如图,在这三人中,此次射击成绩最稳定的是( ) A、甲 B、乙 C、丙 D、无法判断6. 把不等式组 的解集表示在数轴上,正确的是( )A、
A、甲 B、乙 C、丙 D、无法判断6. 把不等式组 的解集表示在数轴上,正确的是( )A、 B、
B、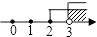 C、
C、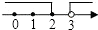 D、
D、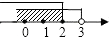 7. 如图1,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
7. 如图1,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( ) A、80° B、50° C、30° D、20°8. 若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为( )A、﹣2 B、2 C、0 D、19. 如图,矩形ABCD的边AB=1,BC=2,以点B为圆心,BC为半径画弧,交AD于点E,则图中阴影部分的面积是( )
A、80° B、50° C、30° D、20°8. 若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为( )A、﹣2 B、2 C、0 D、19. 如图,矩形ABCD的边AB=1,BC=2,以点B为圆心,BC为半径画弧,交AD于点E,则图中阴影部分的面积是( ) A、 B、2 C、 D、2﹣10. 如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是( )
A、 B、2 C、 D、2﹣10. 如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是( )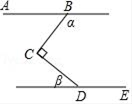 A、α+β=180° B、α+β=90° C、β=3α D、α﹣β=90°11. 图1是甲、乙两个圆柱形水槽,一个圆柱形的空玻璃杯放置在乙槽中(空玻璃杯的厚度忽略不计).将甲槽的水匀速注入乙槽的空玻璃杯中,甲水槽内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2线段DE所示,乙水槽(包括空玻璃杯)内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2折线O﹣A﹣B﹣C所示.记甲槽底面积为S1 , 乙槽底面积为S2 , 乙槽中玻璃杯底面积为S3 , 则S1:S2:S3的值为( )
A、α+β=180° B、α+β=90° C、β=3α D、α﹣β=90°11. 图1是甲、乙两个圆柱形水槽,一个圆柱形的空玻璃杯放置在乙槽中(空玻璃杯的厚度忽略不计).将甲槽的水匀速注入乙槽的空玻璃杯中,甲水槽内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2线段DE所示,乙水槽(包括空玻璃杯)内最高水位y(厘米)与注水时间t(分钟)之间的函数关系如图2折线O﹣A﹣B﹣C所示.记甲槽底面积为S1 , 乙槽底面积为S2 , 乙槽中玻璃杯底面积为S3 , 则S1:S2:S3的值为( ) A、8:5:1 B、8:10:5 C、5:8:3 D、4:5:212. 观察图中正方形四个顶点所标的数字规律,可知数字28应标在( )
A、8:5:1 B、8:10:5 C、5:8:3 D、4:5:212. 观察图中正方形四个顶点所标的数字规律,可知数字28应标在( ) A、第7个正方形的右下角 B、第7个正方形的左下角 C、第8个正方形左下角 D、第8个正方形的右下角13. 如图,内接于半径为5的⊙ , 点B在⊙上,且 , 则下列量中,值会发生变化的量是( )
A、第7个正方形的右下角 B、第7个正方形的左下角 C、第8个正方形左下角 D、第8个正方形的右下角13. 如图,内接于半径为5的⊙ , 点B在⊙上,且 , 则下列量中,值会发生变化的量是( ) A、的度数 B、的长 C、的长 D、弧的长14. 如图,分别以直角三角形的三边为边长向外作等边三角形,面积分别记为S1、S2、S3 , 则S1、S2、S3之间的关系是( )
A、的度数 B、的长 C、的长 D、弧的长14. 如图,分别以直角三角形的三边为边长向外作等边三角形,面积分别记为S1、S2、S3 , 则S1、S2、S3之间的关系是( ) A、 B、 C、 D、15. 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),( , y2)是抛物线上的两点,则y1<y2 . 其中正确的是( )
A、 B、 C、 D、15. 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),( , y2)是抛物线上的两点,则y1<y2 . 其中正确的是( ) A、①②③ B、①③ C、①④ D、①③④16. 如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为的多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
A、①②③ B、①③ C、①④ D、①③④16. 如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为的多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( ) A、﹣2 B、﹣1 C、0 D、1
A、﹣2 B、﹣1 C、0 D、1二、填空题
-
17. 一块直角三角板如图所示放置, , , , 测得边在平面的中心投影长为 , 则长为 , 的面积是 .
 18. 如图所示一张圆形光盘,已知光盘内直径为2cm,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:),那么该光盘的外直径是cm,该光盘的面积是 .
18. 如图所示一张圆形光盘,已知光盘内直径为2cm,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:),那么该光盘的外直径是cm,该光盘的面积是 . 19. 如图,如果边长为1的正六边形绕着顶点顺时针旋转后与正六边形重合.
19. 如图,如果边长为1的正六边形绕着顶点顺时针旋转后与正六边形重合. (1)、则BD的长是;(2)、点在整个旋转过程中,所经过的路径长为(结果保留).
(1)、则BD的长是;(2)、点在整个旋转过程中,所经过的路径长为(结果保留).三、解答题
-
20. 已知关于 , 的二元一次方程组的解满足 , 求的取值范围.21. 【阅读理解】
用 的矩形瓷砖,可拼得一些长度不同但宽度均为 的图案.已知长度为 、 、 的所有图案如下:
 (1)、【尝试操作】
(1)、【尝试操作】如图,将小方格的边长看作 ,请在方格纸中画出长度为 的所有图案.
 (2)、【归纳发现】观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.
(2)、【归纳发现】观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.图案的长度
所有不同图案的个数
22. 小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.23. 如图, 是 的切线,切点为 , 是 的直径,连接 交 于 .过 点作 于点 ,交 于 ,连接 , . (1)、求证: 是 的切线;(2)、求证: 为 的内心;(3)、若 , ,求 的长.24. 如图,在平面直角坐标系xOy中,直线与函数的图象的两个交点分别为A(1,5),B.
(1)、求证: 是 的切线;(2)、求证: 为 的内心;(3)、若 , ,求 的长.24. 如图,在平面直角坐标系xOy中,直线与函数的图象的两个交点分别为A(1,5),B. (1)、求 , 的值;(2)、过点P(n,0)作x轴的垂线,与直线和函数的图象的交点分别为点M,N,当点M在点N下方时,写出n的取值范围.25. 某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
(1)、求 , 的值;(2)、过点P(n,0)作x轴的垂线,与直线和函数的图象的交点分别为点M,N,当点M在点N下方时,写出n的取值范围.25. 某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.销售量p(件)
P=50—x
销售单价q(元/件)
当1≤x≤20时,
当21≤x≤40时,
(1)、请计算第几天该商品的销售单价为35元/件?(2)、求该网店第x天获得的利润y关于x的函数关系式.(3)、这40天中该网店第几天获得的利润最大?最大利润是多少?26. 如图①,在钝角中, , , 点为边中点,点为边中点,将绕点逆时针方向旋转度(). (1)、如图②,当时,连接、 . 求证:;(2)、如图③,直线、交于点 . 在旋转过程中,的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)、将从图①位置绕点B逆时针方向旋转180°,求点的运动路程.
(1)、如图②,当时,连接、 . 求证:;(2)、如图③,直线、交于点 . 在旋转过程中,的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)、将从图①位置绕点B逆时针方向旋转180°,求点的运动路程.