河北省沧州市青县2022年初中毕业生考试一模数学试卷
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列各数中绝对值最大的是( )A、-5 B、0 C、 D、2. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 圆锥的展开图可能是下列图形中的( )A、
3. 圆锥的展开图可能是下列图形中的( )A、 B、
B、 C、
C、 D、
D、 4. 若 , 那么( )A、 , 从左到右是因式分解 B、 , 从左到右是因式分解 C、 , 从左到右是乘法运算 D、 , 从左到右是乘法运算5. 为了疫情防控工作的需要,某学校在门口的大门上方安装了人体体外测温摄像头,当学生站在点B时测得摄像头M的仰角为30°,当学生走到点A时测得摄像头M的仰角为60°,则当学生从B走向A时,测得的摄像头M的仰角为( )
4. 若 , 那么( )A、 , 从左到右是因式分解 B、 , 从左到右是因式分解 C、 , 从左到右是乘法运算 D、 , 从左到右是乘法运算5. 为了疫情防控工作的需要,某学校在门口的大门上方安装了人体体外测温摄像头,当学生站在点B时测得摄像头M的仰角为30°,当学生走到点A时测得摄像头M的仰角为60°,则当学生从B走向A时,测得的摄像头M的仰角为( )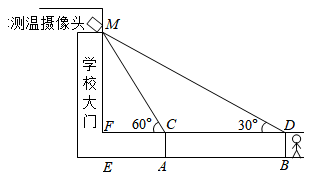 A、越来越小,可能为20° B、越来越大,可能为40° C、越来越大,可能为70° D、走到AB中点时,仰角一定为45°6. 网聚正能量,构建同心圆.以“奋斗的人民奋进的中国”为主题的2021中国正能量“五个一百”网络精品征集评选展播活动进入火热的展播投票阶段.截至2021年11月26日18点,“五个一百”活动投票量累计13909615次,数据13909615用科学记数法表示并精确到百万位为( )A、 B、 C、 D、7. 北京与西班牙的时差为7个小时.比如,北京时间中午12点是西班牙的凌晨5点,2022年2月4日晚8时北京冬奥会开幕式正式开始,在西班牙留学的嘉琪准时观看了直播,直播开始的当地时间为( )A、凌晨1点 B、凌晨3点 C、17:00 D、13:008. 某中学初三年级在开学初和开学一月后进行了两次体能测试(共三项,满分30分),10班学生的两次测试成绩统计如下,则下列成绩分析一定正确的是( )
A、越来越小,可能为20° B、越来越大,可能为40° C、越来越大,可能为70° D、走到AB中点时,仰角一定为45°6. 网聚正能量,构建同心圆.以“奋斗的人民奋进的中国”为主题的2021中国正能量“五个一百”网络精品征集评选展播活动进入火热的展播投票阶段.截至2021年11月26日18点,“五个一百”活动投票量累计13909615次,数据13909615用科学记数法表示并精确到百万位为( )A、 B、 C、 D、7. 北京与西班牙的时差为7个小时.比如,北京时间中午12点是西班牙的凌晨5点,2022年2月4日晚8时北京冬奥会开幕式正式开始,在西班牙留学的嘉琪准时观看了直播,直播开始的当地时间为( )A、凌晨1点 B、凌晨3点 C、17:00 D、13:008. 某中学初三年级在开学初和开学一月后进行了两次体能测试(共三项,满分30分),10班学生的两次测试成绩统计如下,则下列成绩分析一定正确的是( )体能测试
参加人数
中位数
众数
平均数
方差
开学初
50
25.8
28
26.5
0.9
一月后
50
26
28
26.7
0.7
A、两次的平均成绩相同 B、两次成绩的众数相同,所以两次成绩一样好 C、一月后的成绩比开学初的成绩更均衡 D、如果25.5分为优秀,则一月后成绩优秀人数比开学初多9. 如图,数轴上-6,-3与6表示的点分别为M、A、N,点B为线段AN上一点,分别以A、B为中心旋转MA、NB,若旋转后M、N两点可以重合成一点C(即构成△ABC),则点B代表的数可能为( ) A、-1 B、0 C、2.5 D、310. 已知:如图1,四边形ABCD是菱形,在直线AC上找两点E、F,使四边形FBED是菱形,则甲乙两个方案( )
A、-1 B、0 C、2.5 D、310. 已知:如图1,四边形ABCD是菱形,在直线AC上找两点E、F,使四边形FBED是菱形,则甲乙两个方案( ) A、甲对,乙错 B、乙对,甲错 C、甲乙都对 D、甲乙都错11. 已知 , 则x的平方根为( )A、5.835 B、0.5835 C、 D、12. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、
A、甲对,乙错 B、乙对,甲错 C、甲乙都对 D、甲乙都错11. 已知 , 则x的平方根为( )A、5.835 B、0.5835 C、 D、12. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、 B、
B、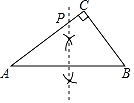 C、
C、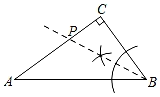 D、
D、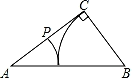 13. 若 , 则的值是( )A、-2 B、2 C、 D、14. 如图,二次函数的图象所在坐标系的原点是( )
13. 若 , 则的值是( )A、-2 B、2 C、 D、14. 如图,二次函数的图象所在坐标系的原点是( ) A、点 B、点 C、点 D、点15. 如图,点A是双曲线在第一象限上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.下列结论:①连接OC,则;②点C在函数上运动.则( )
A、点 B、点 C、点 D、点15. 如图,点A是双曲线在第一象限上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.下列结论:①连接OC,则;②点C在函数上运动.则( ) A、①对②错 B、①错②对 C、①②都对 D、①②都错16. 如图,矩形ABCD中, , △EFG为等腰直角三角形, , 点E、F分别为AB、BC边上的点(不与端点重合), . 现给出以下结论:①;②点G始终在的平分线上;③点G可能在 的平分线上;④点G到边BC的距离的最大值为 . 其中错误的个数是( )
A、①对②错 B、①错②对 C、①②都对 D、①②都错16. 如图,矩形ABCD中, , △EFG为等腰直角三角形, , 点E、F分别为AB、BC边上的点(不与端点重合), . 现给出以下结论:①;②点G始终在的平分线上;③点G可能在 的平分线上;④点G到边BC的距离的最大值为 . 其中错误的个数是( ) A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题
-
17. 已知关于x的方程的解为 , 则a的值为;嘉琪在解该方程去分母时等式右边的-1忘记乘6,则嘉琪解得方程的解为 .18. 量角器如图放置,点、、在一条直线上,点在处,点在处.
 (1)、(填“”“”或“”);(2)、已知量角器(看作半圆)的半径为4cm,点到量角器中心的距离为0.5cm,则 .19. 在平面内有一个正方形,边长为4,中心为O,在正方形内有一动点P, , 设点P到正方形上所有点距离的最大值为d.
(1)、(填“”“”或“”);(2)、已知量角器(看作半圆)的半径为4cm,点到量角器中心的距离为0.5cm,则 .19. 在平面内有一个正方形,边长为4,中心为O,在正方形内有一动点P, , 设点P到正方形上所有点距离的最大值为d. (1)、当△ABP的面积最小时,d的值为;(2)、d的值为 .
(1)、当△ABP的面积最小时,d的值为;(2)、d的值为 .三、解答题
-
20. 计算: .
解法1:原式①
②
③
解法2:原式①
②
③
(1)、解法1是从第步开始出现错误的;解法2是从第步开始出现错误的;(填写序号即可)(2)、请给出正确解答.21. 随着2022年北京-张家口冬奥会的顺利举办,冬奥会吉祥物“冰墩墩”一跃成为冬奥顶流.某玩具生产厂家接到制作3600个“冰墩墩”的订单,但是在实际制作时,实际每天制作的个数是原计划的n倍,结果提前10天完成,求实际每天制作“冰墩墩”的个数.(1)、设实际每天制作“冰墩墩”x个,可得方程 , 则;(2)、若 , 请利用方程解决问题.22. 为积极响应国家提倡的“绿色”“环保”“节能”的人类生活新标准,智能家居逐步进入公众视野.某“智能家居”品牌为扩大知名度,以智能家居的八大系统为内容制作了明信片和精美台历作为奖品进行抽奖活动.工作人员准备了四张标有1,2,3,4的卡片(除数字外完全相同),背面朝上,洗匀放好.顾客从中随机抽取一张后不放回,再从中抽取一张.若顾客抽到的两张卡片恰好有一张是偶数,则奖品是明信片,若两张恰好都是偶数,则奖品是台历.(1)、若顾客小王抽到的第一张卡片是奇数,①小王获得明信片的概率为 ▲ ;
②小王认为如果第一张卡片抽到偶数,获得明信片的概率更高,你同意小王的观点吗?说明理由;
(2)、请用列表或画树状图的方法求顾客获得台历的概率.23. 已知△ABC在平面直角坐标系中的位置如图, , , , 为△ABC的外接圆. (1)、的坐标为;(2)、设弧AC与线段AB、BC所围成的封闭图形的面积为S(图中阴影部分),嘉琪说 , 请通过计算判断嘉琪的说法是否符合题意;(3)、我们把横纵坐标都是整数的点叫做格点.直线l与相切于点B,直接写出直线l经过的图中格点坐标.(切点除外)24. 如图,在平面直角坐标系中,直线 , 直线与x轴分别交于点 , , 与y轴分别交于点D,E,且与交于点C.
(1)、的坐标为;(2)、设弧AC与线段AB、BC所围成的封闭图形的面积为S(图中阴影部分),嘉琪说 , 请通过计算判断嘉琪的说法是否符合题意;(3)、我们把横纵坐标都是整数的点叫做格点.直线l与相切于点B,直接写出直线l经过的图中格点坐标.(切点除外)24. 如图,在平面直角坐标系中,直线 , 直线与x轴分别交于点 , , 与y轴分别交于点D,E,且与交于点C. (1)、求k,b的值和线段DE的长度;(2)、求△CDE与△ABC的面积差;(3)、点Q以每秒个单位的速度从点E出发沿直线向右上方匀速运动,点P同时从点D出发,沿向右下方匀速运动,并一直保持轴.通过计算说明线段PQ的长度不超过2个单位时的时长是多少.25. 为满足居民电动车的充电需求,新华区联盟街道办联手社区召开增设充电桩专项行动,要求每个小区全覆盖.居委会人员周六调研了联强小区2号存车棚7:00至19:00各时段的存放、取走电动车数,以及整点时刻的电动车总数(称为存量)情况,表格中时的y值表示8:00时的存量,时的y值表示9:00时的存量…依次类推.他们发现存量y(辆)与x(x为整数)满足如下图所示的一个二次函数关系.
(1)、求k,b的值和线段DE的长度;(2)、求△CDE与△ABC的面积差;(3)、点Q以每秒个单位的速度从点E出发沿直线向右上方匀速运动,点P同时从点D出发,沿向右下方匀速运动,并一直保持轴.通过计算说明线段PQ的长度不超过2个单位时的时长是多少.25. 为满足居民电动车的充电需求,新华区联盟街道办联手社区召开增设充电桩专项行动,要求每个小区全覆盖.居委会人员周六调研了联强小区2号存车棚7:00至19:00各时段的存放、取走电动车数,以及整点时刻的电动车总数(称为存量)情况,表格中时的y值表示8:00时的存量,时的y值表示9:00时的存量…依次类推.他们发现存量y(辆)与x(x为整数)满足如下图所示的一个二次函数关系.时段
存放车数(辆)
取走车数(辆)
存量y(辆)
7:00-8:00
1
45
5
8:00-9:00
2
43
11
132
…
…
…
…
…
根据所给图表信息,解决下列问题:
 (1)、m=;(2)、求整点时刻的电动车存量y与x之间满足的二次函数关系式;(3)、车棚存量最多时有多少辆电动车?是哪个时段?(4)、居委会人员小王在某个整点时刻统计车辆数目时,发现车棚的电动车不到100辆,请直接写出他去车棚的时间可能是几点.26. 在△ABC中, , 点D是边BC上一动点,连接AD,将AD绕点A逆时针旋转至AE,使 . 论证:如图1,当时,连接CE、BE,其中BE交AC于点F.探索:如图2,连接BE,取BE的中点G,连接AG.设 .
(1)、m=;(2)、求整点时刻的电动车存量y与x之间满足的二次函数关系式;(3)、车棚存量最多时有多少辆电动车?是哪个时段?(4)、居委会人员小王在某个整点时刻统计车辆数目时,发现车棚的电动车不到100辆,请直接写出他去车棚的时间可能是几点.26. 在△ABC中, , 点D是边BC上一动点,连接AD,将AD绕点A逆时针旋转至AE,使 . 论证:如图1,当时,连接CE、BE,其中BE交AC于点F.探索:如图2,连接BE,取BE的中点G,连接AG.设 . (1)、求证:;(2)、若BE平分 , 求证:;(3)、用含x的代数式表示CD的长;(4)、如图3,若 , , 连接DE,DG,CE.当时,请直接写出DE的长.
(1)、求证:;(2)、若BE平分 , 求证:;(3)、用含x的代数式表示CD的长;(4)、如图3,若 , , 连接DE,DG,CE.当时,请直接写出DE的长.