河北省保定市清苑区2022年中考一模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，为无理数的是（）

A、-5 B、0 C、 $\frac{2}{3}$ D、 $\sqrt{7}$

查看试题解析
2. 如图，设点P是直线l外一点， $P Q ⊥ l$ ，垂足为点Q，点T是直线l上的一个动点，连接 $P T$ ，则（）

A、 $P T < P O$ B、 $P T > T Q$ C、 $P T ≥ P Q$ D、 $P T ≤ P Q$

查看试题解析
3. 若表示实数a的点A在数轴上的位置如图所示，则下列说法正确的是（）

A、a是正整数 B、a的相反数是-2 C、a的倒数是 $- \frac{1}{2}$ D、a的绝对值是1

查看试题解析
4. 如图，小明手持激光灯照向地面，激光灯发出的光线 $C O$ 与地面 $A B$ 形成了两个角， $∠ B O C = 5 ∠ A O C$ ，则 $∠ B O C$ 的度数是（）

A、160° B、150° C、120° D、20°

查看试题解析
5. 下列运算中正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $3 a^{2} b - 3 b a^{2} = 0$ C、 $2 x^{3} + 3 x^{2} = 5 x^{5}$ D、 $5 y^{2} - 4 y^{2} = 1$

查看试题解析
6. 某种计算机完成1次基本运算的时间约为1纳秒（ns），已知 $1 n s = 0.000000001 s$ ，该计算机完成5次基本运算，所用时间用科学记数法表示为（）

A、 $0.5 \times 1 0^{- 9}$ B、 $5 \times 1 0^{- 9}$ C、 $0.5 \times 1 0^{- 8}$ D、 $5 \times 1 0^{- 10}$

查看试题解析
7. 在“爱我河北”白色垃圾清理活动中，小霞同学从B点出发，沿北偏西20°方向到达C地，已知 $∠ C = 70 °$ ，此时营地A在C的（）

A、北偏东20°方向上 B、北偏东70°方向上 C、南偏西50°方向上 D、北偏西70°方向上

查看试题解析
8. 一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的体积为（）

A、12 B、16 C、18 D、24

查看试题解析
9. 根据数值转换机的示意图，输出的值为（）

A、9 B、-9 C、 $\frac{1}{9}$ D、 $- \frac{1}{9}$

查看试题解析
10. 已知线段AB，按如下步骤作图：①作射线AC，使AC⊥AB；②作∠BAC的平分线AD；③以点A为圆心，AB长为半径作弧，交AD于点E；④过点E作EP⊥AB于点P，则AP：AB=（）

A、 $1 ： \sqrt{5}$ B、 $1 ： 2$ C、 $1 ： \sqrt{3}$ D、 $1 ： \sqrt{2}$

查看试题解析
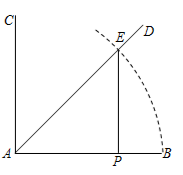11. 小明去商店购买A、B两种玩具，共用了10元钱，A种玩具每件1元，B种玩具每件2元.若每种玩具至少买一件，且A种玩具的数量多于B种玩具的数量.则小明的购买方案有（）

A、5种 B、4种 C、3种 D、2种

查看试题解析
12. 李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是 $($ $)$
已知：如图，在 $△ A B C$ 中，点D，E，F分别在边AB，AC，BC上，且 $D E / / B C$ ， $D F / / A C$ ，
求证： $△ A D E$ ∽ $△ D B F$ ．
证明： $①$ 又 $∵ D F / / A C$ ， $② ∵ D E / / B C$ ， $③ ∴ ∠ A = ∠ B D F$ ， $④ ∴ ∠ A D E = ∠ B$ ， $∴ △ A D E$ ∽ $△ D B F$ ．

A、 $③ ② ④ ①$ B、 $② ④ ① ③$ C、 $③ ① ④ ②$ D、 $② ③ ④ ①$

查看试题解析
13. 已知 $△ A B C$ 和 $△ A B D$ 有相同的外心， $∠ D = 70 °$ ，则 $∠ C$ 的度数是（）

A、70° B、110° C、70°或110° D、不能确定

查看试题解析
14. 已知分式： $(a + \frac{3 a - 4}{a - 3}) (■ - \frac{1}{a - 2})$ 的某一项被污染，但化简的结果等于 $a + 2$ ，被污染的项应为（）

A、0 B、1 C、 $\frac{a - 2}{a - 3}$ D、 $\frac{a - 3}{a - 2}$

查看试题解析
15. 如图，在平面直角坐标系 $x O y$ 中，横纵坐标都为整数的点称为整点，等边三角形 $△ A O B$ 的顶点A在第一象限，点 $B (3 ， 0)$ ，双曲线 $y = \frac{k}{x}$ $(k > 0 ， x > 0)$ 把 $△ A O B$ 分成两部分，若这两部分内的整点个数相等（不含边界），则k的取值范围为（）

A、 $1 < k < 2$ B、 $1 \leq k \leq 2$ C、 $0 < k < 1$ D、 $0 \leq k \leq 1$

查看试题解析
16. 如图，在矩形ABCD中， $A B = 15$ ， $B C = 20$ ，把边AB沿对角线BD平移，点 $A'$ ， $B'$ 分别对应点A，B.给出下列结论：①顺次连接点 $A'$ ， $B'$ ，C，D的图形是平行四边形；②点C到它关于直线 $A A'$ 的对称点的距离为48；③ $A' C - B' C$ 的最大值为15；④ $A' C + B' C$ 的最小值为 $9 \sqrt{17}$ .其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

17. 如图，在平面直角坐标系中，有一个由四个边长为1的正方形组成的图案，其中点A坐标为 $(3 ， 7)$ ，则点B坐标为．

查看试题解析
18. 2021年是中国共产党成立100周年，某校举行“喜迎中国共产党建党100周年”党史知识竞赛，如表是11名决赛选手的成绩．这11名决赛选手成绩的中位数是，如果再加一位选手参加决赛，加上这位选手的成绩后，发现12名选手与之前11位选手的成绩的中位数一样．设最后参赛选手的成绩是m分，则m的取值范围是．
分数
100
95
90
85
人数
1
5
3
2

查看试题解析
19. 某厂家要设计一个装彩铅的纸盒，已知每支笔形状、大小相同，底面均为正六边形，六边形边长为1cm. 目前厂家提供了圆形和等边三角形两种作为底面的设计方案，我们以6支彩铅为例，可以设计如图的两种收纳方案：

(1)、如果要装6支彩铅，在以上两种方案里，你认为更小的底面积是cm.

(2)、如果你要装12只彩铅，要求相邻彩铅拼接无空隙，请设计一种最佳的布局，并使用圆形来设计底面，则底面半径的最小值为cm.

查看试题解析

三、解答题

20. 如图，在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛．若圆形的半径为 $r m$ ，广场长为 $a m$ ，宽为 $b m$ ．

(1)、列式表示广场空地的面积；

(2)、若广场的长为 $500 m$ ，宽为 $200 m$ ，圆形花坛的半径为 $20 m$ ，求广场空地的面积（计算结果保留 $π$ ）．

查看试题解析
21. 图①、图②是某月的月历

(1)、图①中带阴影的方框中的9个数之和与方框正中心的数有什么关系？请说明理由．

(2)、如果将带阴影的方框移至图②的位置，（1）中的关系还成立吗？若成立，说明理由．

(3)、甲同学说，所求的9个数之和可以是90，乙同学说，所求的9个数之和也可以是290，甲、乙的说法对吗？若对，求出方格中最中间的一个数，若不对，说明理由．

查看试题解析

22. 疫苗接种初期，为更好地响应国家对符合条件的人群接种新冠疫苗的号召，某市教育部门随机抽取了该市部分七、八、九年级教师，了解教师的疫苗接种情况，得到如下统计表：

	已接种	未接种	合计
七年级	30	10	40
八年级	35	15	$a$
九年级	40	$b$	60
合计	105	$c$	150

(1)、表中，

a =

，

b =

，

c =

；

(2)、由表中数据可知，统计的教师中接种率最高的是年级教师；（填“七”或“八”或“九”）

(3)、若该市初中七、八、九年级一共约有8000名教师，根据抽样结果估计未接种的教师约有人；

(4)、为更好地响应号召，立德中学从最初接种的4名教师（其中七年级1名，八年级1名，九年级2名）中随机选取2名教师谈谈接种的感受，请用列表或画树状图的方法，求选中的两名教师恰好不在同一年级的概率.

查看试题解析

23. 如图， $A C$ 是⊙O的直径， $O D ⊥ A B$ ，点E是射线 $D O$ 上一点且 $O E = B C$ ，过点E作 $F E ⊥ D E$ 交射线 $A C$ 于点F．

(1)、求证： $O E = 2 O D$ ；

(2)、求证： $△ A B C ≌ △ F E O$ ；

(3)、当 $E F$ 与⊙O相切时，若⊙O的半径为2，求弧 $B C$ 的长．

查看试题解析
24. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象直线经过点 $A (- 2 ， 6)$ ，且与x轴、y轴分别相交于点B、D，与正比例函数 $y = 3 x$ 的图象直线 $l_{2}$ 交于点C，点C的横坐标为1．

(1)、求k、b的值；

(2)、直线 $x = a$ 与直线 $l_{1}$ ， $l_{2}$ 分别相交于点E、F，且点E与F关于x轴对称．求a的值；

(3)、若一次函数 $y = m x + m$ 的图象直线 $l_{3}$ 与线段 $C D$ 有交点，直接写出m的取值范围．

查看试题解析
25. 某工艺品厂生产一种汽车装饰品，每件生产成本为20元，销售价格在30元至80元之间（含30元和80元），销售过程中的管理、仓储、运输等各种费用（不含生产成本）总计50万元，其销售量y（万个）与销售价格（元/个）的函数关系如图所示.

(1)、当30≤x≤60时，求y与x的函数关系式；

(2)、求出该厂生产销售这种产品的纯利润w（万元）与销售价格x（元/个）的函数关系式；

(3)、销售价格应定为多少元时，获得利润最大，最大利润是多少？

查看试题解析
26. 课本再现

(1)、在证明“三角形内角和定理”时，小明只撕下三角形纸片的一个角拼成图1即可证明，其中与 $∠ A$ 相等的角是；

(2)、类比迁移
如图2，在四边形 $A B C D$ 中， $∠ A B C$ 与 $∠ A D C$ 互余，小明发现四边形 $A B C D$ 中这对互余的角可类比（1）中思路进行拼合：先作 $∠ C D F = ∠ A B C$ ，再过点 $C$ 作 $C E ⊥ D F$ 于点 $E$ ，连接 $A E$ ，发现 $A D$ ， $D E$ ， $A E$ 之间的数量关系是；

(3)、方法运用

如图3，在四边形 $A B C D$ 中，连接 $A C$ ， $∠ B A C = 90 °$ ，点 $O$ 是 $△ A C D$ 两边垂直平分线的交点，连接 $O A$ ， $∠ O A C = ∠ A B C$ ．

①求证： $∠ A B C + ∠ A D C = 90 °$ ；

②连接 $B D$ ，如图4，已知 $A D = m$ ， $D C = n$ ， $\frac{A B}{A C} = 2$ ，求 $B D$ 的长（用含 $m$ ， $n$ 的式子表示）．

查看试题解析

分数	100	95	90	85
人数	1	5	3	2