广东省深圳市光明区2022年五月份中考二模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. -2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 第七次人口普查结果显示，光明区常住人口达到109万，成为深圳市最具人口活力的区域之一，其中109万用科学记数法表示为（）

A、1.09×10² B、1.09×10⁶ C、10.9×10² D、10.9×10⁵

查看试题解析
3. 观察下列图形，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算中，正确的是（）

A、a⁸÷a²＝a⁴ B、（a³）⁴＝a¹² C、（﹣3a）²＝a⁶ D、3a²•a³＝3a⁶

查看试题解析
5. 学校课后延时服务项目为同学们提供了丰富多彩的课程，欢欢从国际象棋、玩转发明、美术欣赏、艺术体操四个社团中任选一个参加，则恰好选到艺术体操社团的概率为（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
6. 下列命题中，是真命题的是（）

A、三角形的外心是三角形三个内角的角平分线的交点 B、过一点有且只有一条直线与已知直线平行 C、连接对角线相等的四边形各边中点所得四边形是矩形 D、一组对边平行，一组对角相等的四边形是平行四边形

查看试题解析
7. 如图，在△AOB中，∠B＝30°，将△AOB绕点O逆时针旋转55°得到△MON，MN与OB交于点G，则∠BGN的度数为（）

A、55° B、75° C、85° D、95°

查看试题解析
8. 如图，在Rt△ABC中，∠C＝90°，AC＝5，⊙O是△ABC的内切圆，半径为2，则图中阴影部分的面积为（）

A、30﹣4π B、 $30 \sqrt{3} - 4 π$ C、60﹣16π D、 $30 \sqrt{3} - 16 π$

查看试题解析
9. 在边长为1的正方形网格中，点A、B、C、D都在格点上，AB与CD相交于点O，则∠AOD的正弦值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
10. 已知二次函数y＝ax²+bx+c（a≠0）的图象与x轴交于A（m，0），B（n，0）两点，已知m+n＝4，且﹣4≤m≤﹣2．图象与y轴的正半轴交点在（0，3）与（0，4）之间（含端点）．给出以下结论：①6≤n≤8；②对称轴是直线x＝2；③当 $a = - \frac{3}{32}$ 时，抛物线的开口最大；④二次函数的最大值可取到6．其中正确结论的个数为（）个

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

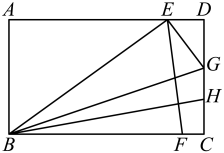
11. 分解因式：4a²﹣16= ．

查看试题解析
12. 一组数据：5，6，5，3，7的中位数是．

查看试题解析
13. 估算在日常生活和数学学习中有着广泛的应用，例如估算数 $\sqrt{2}$ ，容易发现 $\sqrt{1} < \sqrt{2} < \sqrt{4}$ ，即 $1 < \sqrt{2} < 2$ ．于是 $\sqrt{2}$ 的整数部分是1，小数部分是 $\sqrt{2} - 1$ ．现记 $\sqrt{15}$ 的整数部分是a，小数部分是b，计算（a﹣b）（b+9）的结果为．

查看试题解析
14. 如图，一次函数y＝x+k（k＞0）的图象与x轴和y轴分别交于点M，N，与反比例函数 $y = \frac{k}{x}$ 的图象在第一象限内交于点B，过点B作BA⊥x轴，BC⊥y轴．垂足分别为点A，C．当矩形OABC与△OMN的面积相等时，点B的坐标为．

查看试题解析
15. 如图，在矩形ABCD中，E为AD上的一点，且BE＝BC＝10，作∠EBC的平分线交CD于点G，CG＝5，F为BC上的一点，H为CG上的一点，且EF⊥BH，给出以下结论，其中正确的结论有．（将你认为正确结论的序号都填上）
①GE＝GC；
②△ABE的面积为24；
③EF：BH＝3：4；
④连接FH，则FH的最小值为 $\frac{20 \sqrt{41}}{41}$ ．

查看试题解析

三、解答题

16. 计算： $（ π - 3 ）^{0} + \sqrt{2} c o s 45 ° - | - 3 | + （ \frac{1}{2} ）^{- 2}$ ．

查看试题解析
17. 先化简，再求值： $(1 - \frac{2}{x + 1}) \div \frac{x^{2} - 2 x + 1}{2 x + 2}$ ，其中﹣2＜x＜2且x为整数．

查看试题解析
18. 4月23日是世界读书日，某学校为增进同学们对中国古诗词的热爱，举行“春季校园飞花令”专场比赛．在预选赛后，学校对参赛同学获奖情况进行统计，绘制了如下两幅不完整的统计图．请结合图中相关数据解答下列问题：

(1)、请将条形统计图补充完整；

(2)、在扇形统计图中，“三等奖”所对应的扇形圆心角的度数为；

(3)、若获得一等奖的同学中有 $\frac{1}{4}$ 来自七年级， $\frac{1}{2}$ 来自九年级，其余的来自八年级，学校决定从获得一等奖的同学中任选两名同学参加全市诗词大会比赛，请通过列表或树状图方法求所选两名同学中，恰好都来自九年级的概率．

查看试题解析
19. 如图，AB是⊙O的直径，N是⊙O上一点，M是 $\overset{⌢}{A N}$ 的中点，连接AN，BM，交于点D．连接NM，OM，延长OM至点C，并使∠CAN＝2∠N．AN与OC交于点E．

(1)、求证：AC是⊙O的切线；

(2)、若DM＝10， $t a n N = \frac{3}{4}$ ，求⊙O的半径．

查看试题解析
20. 九（1）班同学在社会实践调研活动中发现，某服装店销售A，B两种款式的衬衫，进价和售价如表所示：
项目
进价（元/件）
售价（元/件）
A
100
120
B
150
200
已知该服装店购进A，B两种款式的衬衫共花费6000元，销售完成后共获得利润1600元．

(1)、服装店购进A，B两种款式的衬衫各多少件？

(2)、若服装店再次购进A，B两种款式的衬衫共30件，其中B款式的数量不多于A款式数量的2倍，且两种衬衫总利润不低于1140元．问共有几种购进方案？请写出利润最大的购进方案．

查看试题解析
21. 如图

(1)、【问题提出】如图（1），每一个图形中的小圆圈都按一定的规律排列，设每条边上的小圆圈个数为a，每个图形中小圆圈的总数为S．
请观察思考并完成以下表格的填写：
a
1
2
3
4
5
…
8
…
S
1
3
6
…
…

(2)、【变式探究】请运用你在图（1）中获得的经验，结合图（2）中小圆圈的排列规律，写出第n个图形的小圆圈总数S与n之间的关系式．

(3)、【应用拓展】生物学家在研究时发现，某种细胞的分裂规律可用图（3）的模型来描述，请写出经过n轮分裂后细胞总数W与n的关系式．并计算经过若干轮分裂后，细胞总数能否达到1261个，若能，求出n的值；若不能，说明理由．

查看试题解析
22. 如图
如图（1），在Rt△ABC中，∠C＝90°，边AC＝8，BC＝6，点M、N分别在线段AC、BC上，将△ABC沿直线MN翻折，点C的对应点是C′．

(1)、当M、N分别是所在边的中点时，求线段CC′的长度；

(2)、若CN＝2，求点C′到线段AB的最短距离；

(3)、如图（2），当点C′落在边AB上时，
①四边形CMC′N能否成为正方形？若能，求出CM的值；若不能，说明理由．
②请直接写出点C′运动的路程长度．

查看试题解析

项目	进价（元/件）	售价（元/件）
A	100	120
B	150	200

a	1	2	3	4	5	…	8	…
S	1	3	6			…		…