广东省深圳市宝安区2022年中考数学二模试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣ $\frac{1}{3}$ 的倒数是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 2月4日，正值立春，2022年北京冬季奥运会开幕式在国家体育场“鸟巢”隆重举行．开幕式以“构建人类命运共同体”为核心表达，立足于从全世界的角度展望美好未来．共有91个国家和地区的代表团参加本届冬奥会，下列图形是个别代表团国旗，其中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. “哪有什么岁月静好，不过是有人替你负重前行．”自壬寅除夕以来，新冠疫情反复肆虐着深圳，一批批“逆行者”化身为天使白、守护蓝和志愿红，冲锋在防疫第一线，为2000万深圳人民筑起了“生命的安全线”．其中“2000万”用科学记数法表示为（）

A、 $2 \times 10^{7}$ B、 $2 \times 10^{8}$ C、 $0.2 \times 10^{8}$ D、 $20 \times 10^{6}$

查看试题解析
4. 下列运算中，正确的是（）

A、2a+a²＝2a³ B、a⁶÷a²＝a³ C、（3a²）²＝3a⁴ D、m³•（﹣m）²＝m⁵

查看试题解析
5. 在一个不透明的袋中装有6个只有颜色不同的球，其中红球3个、黄球2个和白球1个，从袋中任意摸出一个球，是黄球的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
6. 如图，在菱形 $A B C D$ 中， $∠ A B C = 70 °$ ，对角线 $A C$ 、 $B D$ 相交于点O，E为 $B C$ 中点，则 $∠ C O E$ 的度数为（）

A、70° B、65° C、55° D、35°

查看试题解析
7. 下列说法中，正确的是（）

A、若 $a^{2} > b^{2}$ ，则 $a > b$ B、位似图形一定相似 C、对于 $y = - \frac{2}{x}$ ，y随x的增大而增大 D、三角形的一个外角等于两个内角之和

查看试题解析
8. 《孙子算经》记载：今有人盗库绢，不知所失几何？但闻草中分绢：人得六匹，盈六匹；人得七匹，不足七匹．问：人、绢各几何？意思是：如果每个人分6匹，还多出6匹，每个人分7匹，还差7匹，问：现在有多少人，有多少匹绢？设现在有x人，有绢y匹，下列所列方程（组）正确的是（）

A、 $6 x - 6 = 7 x + 7$ B、 $6 x + 6 = 7 x - 7$ C、 ${\begin{array}{l} y = 6 x + 6 \\ y - 7 = 7 x \end{array}$ D、 ${\begin{array}{l} y = 6 x - 6 \\ y + 7 = 7 x \end{array}$

查看试题解析
9. 如图， $⊙ O$ ， $⊙ O_{1}$ 都经过A、B两点，且点O在 $⊙ O_{1}$ 上，连接 $A O$ 并延长，交 $⊙ O$ 于点C，连接 $B C$ 交 $⊙ O_{1}$ 于点D，连接 $A D$ ， $A D ⊥ B O$ ，若 $A B = 3$ ，则 $\overset{⌢}{B D}$ 的长为（）

A、 $\frac{π}{2}$ B、 $\frac{2}{3} π$ C、 $\frac{\sqrt{3}}{2} π$ D、 $\frac{\sqrt{3}}{3} π$

查看试题解析
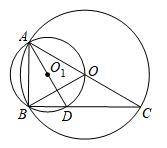10. 已知（x₁ ， y₁），（x₂ ， y₂）（x₁＜x₂）是抛物线y＝x²﹣2tx﹣1上两点，以下四个命题：①若y的最小值为﹣1，则t＝0；②点A（1，﹣2t）关于抛物线对称轴的对称点是B（2t﹣1，﹣2t）；③当t≤1时，若x₁+x₂＞2，则y₁＜y₂；④对于任意的实数t，关于x的方程x²﹣2tx＝1﹣m总有实数解，则m≥﹣1，正确的有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
12. 已知 $x = - 1$ 是方程 $x^{2} + 2 x - m = 0$ 的一个根，则m的值为．

查看试题解析
13. “湾区之光”摩天轮位于深圳市华侨城欢乐港湾内，是深圳地标性建筑之一．摩天轮采用了世界首创的鱼鳍状异形大立架，有28个进口轿厢，每个轿厢可容纳25人．小亮在轿厢B处看摩天轮的圆心O处的仰角为30°，看地面A处的俯角为45°（如图所示， $O A$ 垂直于地面），若摩天轮的半径为54米，则此时小亮到地面的距离 $B C$ 为米．（结果保留根号）

查看试题解析
14. 定义： $\max (x ， y) = {\begin{array}{l} x & (x \geq y) \\ y & (x \leq y) \end{array}$ ，例如： $\max (2 ， 1) = 2$ ， $\max (a^{2} ， a^{2} + 1) = a^{2} + 1$ ，当 $x > 0$ 时，函数 $y = \max (\frac{2}{x} ， x + 1)$ 的最小值为．

查看试题解析
15. 图，在▱ABCD中，对角线AC，BD交于点O，AF平分∠BAC，交BD于点E，交BC于点F，若BE＝BF＝2，则AD＝．

查看试题解析

三、解答题

16. 计算： $- 1^{2022} + | \sqrt{3} - 2 | + 2 \cos 30 ° + {(\frac{1}{2})}^{- 2}$

查看试题解析
17. 先化简，后求值： $(\frac{1}{x - 2} + 1) \div \frac{x^{2} - 2 x + 1}{x^{2} - x}$ ，从 $- 1$ ，0，1，2选一个合适的值，代入求值．

查看试题解析
18. 睡眠是机体复原整合和巩固记忆的重要环节，对促进中小学生大脑发育、骨骼生长、视力保护、身心健康和提高学习能力与效率至关重要．为了解教育部发布的《关于进一步加强中小学生睡眠管理工作的通知》的实施成效，某调查组随机调查了某学校部分初中生的睡眠时间，假设平均每天的睡眠时间为x小时，为了方便统计，当 $6 \leq x < 7$ 时记为6小时，当 $7 \leq x < 8$ 时记作7小时，以此类推……根据调查数据绘制了以下不完整的统计图：

根据图中信息回答下列问题：

(1)、本次共调查了 ▲ 名学生，请将条形统计图补充完整；

(2)、本次抽查的学生平均每天睡眠时间的众数为，中位数为；

(3)、平均每天睡眠时间为7小时所对应的圆心角的度数为°；

(4)、根据“通知”要求，初中生睡眠时间要达到9小时该．校有1800名学生，根据抽样调查结果，估计该校有名学生平均每天睡眠时间低于9小时．

查看试题解析

19. 在并联电路中，电源电压为

U_{总} = 6 V

，小亮根据“并联电路分流不分压”的原理知道：

I_{总} = I_{1} + I_{2}

（

I_{1} = \frac{6}{R_{1}}

，

I_{2} = \frac{6}{R}

）．已知R₁为定值电阻，当R变化时，干路电流

I_{总}

也会发生变化，且干路电流

I_{总}

与R之间满足如下关系：

I_{总} = 1 + \frac{6}{R}

．

(1)、定值电阻

R_{1}

的阻值为

Ω

；

(2)、小亮根据学习函数的经验，参照研究函数的过程与方法，对比反比例函数

I_{2} = \frac{6}{R}

来探究函数

I_{总} = 1 + \frac{6}{R}

的图象与性质．

①列表：下表列出 $I_{总}$ 点与R的几组对应值，请写出m，n的值： $m =$ ， $n =$ ；

R	…	3	4	5	6	…
$I_{2} = \frac{6}{R}$	…	2	1.5	1.2	1	…
$I_{总} = 1 + \frac{6}{R}$	…	3	m	2.2	n	…

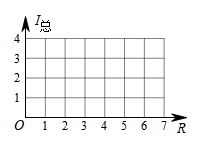
②描点、连线：在平面直角坐标系中，以①给出的R的取值为横坐标，以 $I_{总}$ 相对应的值为纵坐标，描出相应的点，并将各点用光滑曲线顺次连接起来；

(3)、观察图象并分析表格，回答下列问题：

① $I_{总}$ 随R的增大而；（填“增大”或“减小”）

②函数 $I_{总} = 1 + \frac{6}{R}$ 的图象是由 $I_{2} = \frac{6}{R}$ 的图象向平移个单位而得到．

查看试题解析

20. 2022年3月12日是第44个植树节，某街道办现计划采购樟树苗和柳树苗共600棵，已知一棵柳树苗比一棵樟树苗贵4元，用2400元所购买的樟树苗与用3200所购买的柳树苗数量相同．

(1)、请问一棵樟树苗的价格是多少元？

(2)、若购买樟树苗的数量不超过柳树苗的2倍，怎样采购所花费用最少？最少多少元？

查看试题解析
21. 在四边形 $A B C D$ 中， $∠ E A F = \frac{1}{2} ∠ B A D$ （E、F分别为边 $B C$ 、 $C D$ 上的动点）， $A F$ 的延长线交 $B C$ 延长线于点M， $A E$ 的延长线交 $D C$ 延长线于点N．

(1)、如图①，若四边形 $A B C D$ 是正方形，求证： $△ A C N ∽ △ M C A$ ；

(2)、如图②，若四边形 $A B C D$ 是菱形，
①（1）中的结论是否依然成立？请说明理由；

②若 $A B = 8$ ， $A C = 4$ ，连接 $M N$ ，当 $M N = M A$ 时，求 $C E$ 的长．

查看试题解析
22. 如图，抛物线 $y = - \frac{3}{4} x^{2} + b x + c$ 交x轴于 $A (- 1 ， 0)$ ， $B (4 ， 0)$ 两点，交y轴于点C，点D是抛物线上位于直线 $B C$ 上方的一个动点．

(1)、求抛物线的解析式；

(2)、连接 $A C$ ， $B D$ ，若 $∠ A B D = ∠ A C B$ ，求点D的坐标；

(3)、在（2）的条件下，将抛物线沿着射线 $A D$ 平移m个单位，平移后A、D的对应点分别为M、N，在x轴上是否存在点P，使得 $△ P M N$ 是等腰直角三角形？若存在，请求出m的值；若不存在，请说明理由．

查看试题解析