广东省广州市南沙区2022年中考数学一模试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 9的算术平方根是（）

A、±3 B、3 C、﹣3 D、±9

查看试题解析
2. 如图所示的几何体是由4个相同的小正方体搭成的，它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 化简m+n﹣（m﹣n）的结果是（）

A、2m B、2n C、﹣2m D、﹣2n

查看试题解析
4. 已知一次函数 $y = k x - 3$ 且 $y$ 随 $x$ 的增大而增大，那么它的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 某城市3月份某星期7天的最低气温如下（单位℃）：17，16，20，18，16，18，18，这组数据的中位数、众数分别是（）

A、16，16 B、16，20 C、18，20 D、18，18

查看试题解析
6. 若代数式 $\frac{\sqrt{x}}{x - 2}$ 有意义，则实数x的取值范围是（）

A、x＞0 B、x≥0 C、x＞0且x≠2 D、x≥0且x≠2

查看试题解析
7. 根钢管放在V形架内，如图是其截面图，O为钢管的圆心，如果钢管的直径为20cm，∠MPN＝60°，则OP的长度是（）

A、40 $\sqrt{3}$ cm B、40cm C、20 $\sqrt{3}$ cm D、20cm

查看试题解析
8. 如图，把△ABC绕着点A顺时针转40°，得到△ADE，若点E恰好在边BC上，AB⊥DE于点F，则∠BAE的大小是（）

A、10° B、20° C、30° D、40°

查看试题解析
9. 若16m+2＜0，则关于x的方程mx²﹣（2m+1）x+m﹣1＝0的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
10. 如图，在平面直角坐标系中，矩形ABCD的顶点A，B分别在y轴的正半轴和x轴的正半轴上，当B在x轴的正半轴上运动时，A随之在y轴的正半轴上运动，矩形ABCD的形状保持不变．若∠OAB＝30°时，点A的纵坐标为2 $\sqrt{3}$ ，点C的纵坐标为1，则点D到点O的最大距离是（）

A、2 $\sqrt{5}$ B、2 $\sqrt{2} +$ 2 C、2 $\sqrt{2} +$ 4 D、2 $\sqrt{3} +$ 4

查看试题解析

二、填空题

11. △ABC中，已知∠A＝50°，∠B＝60°，则∠C的外角的度数是．

查看试题解析
12. 单项式 $- 3 x^{2} y$ 的次数是.

查看试题解析
13. 已知反比例函数y $= \frac{k - 2}{x}$ （k是常数，且k≠2）的图象有一支在第三象限，那么k的取值范围是．

查看试题解析
14. 如图，⊙O的直径为10，弦AB＝8，P是弦AB上一动点，那么OP长的取值范围是.

查看试题解析
15. 如图，广州塔与木棉树间的水平距离BD为600m，从塔尖A点测得树顶C点的俯角α为44°，测得树底D点俯角β为45°，则木棉树的高度CD是．（精确到个位，参考数据：sin44°≈0.69，cos44°≈0.72，tan44°≈0.96）

查看试题解析
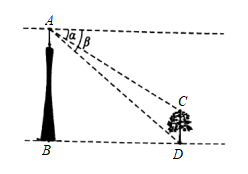16. 如图，在平行四边形ABCD中，∠BAD＝60°，延长AD至点E使得AE＝AB，连接BE交CD于点F，连接并延长AF，交CE于点G．下列结论：①△BAD≌△EBC；②BD＝AF；③BD⊥AG；④若AD＝2DE，则 $\frac{F G}{C G} = \frac{1}{2}$ ．其中，正确的结论是．（请填写所有正确结论的序号）

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 2 x - 1 > x + 1 \\ x + 8 < 4 x - 1 \end{array}$ .

查看试题解析
18. 如图，点E、C在线段BF上，AC∥DF，∠A＝∠D，AB＝DE，证明：BE＝CF．

查看试题解析
19. 已知 $T = \frac{{(x + 2)}^{2}}{x^{2} - 4} - \frac{x}{x - 2}$ ．

(1)、化简T；

(2)、若点（x，0）在二次函数y＝（x+1）（x+2）的图象上，求T的值．

查看试题解析
20. 某校为落实《青少年体育活动促进计划》，为学生“每天体育锻炼1小时”创造更好的条件，计划从体育用品店购进一批足球、篮球和排球．已知同一种球单价相同，一个排球单价为80元，若购买3个足球和2个排球共需400元，购买2个足球和3个篮球共需610元．

(1)、求购买一个足球、一个篮球和一个排球共需多少元？

(2)、学校根据需求计划从体育用品店一次性购买三种球共100个，且购买的三种球的费用不超过12000元，求该学校最多可以购买多少个篮球？

查看试题解析
21. 某校对九年级学生参加体育“五选一”自选项目测试进行抽样调查，调查学生所报自选项目的情况统计如下：
自选项目
立定跳远
三级蛙跳
跳绳
实心球
铅球
人数/人
9
13
8
b
4
频率
a
0.26
0.16
0.32
0.08

(1)、a＝， b＝．

(2)、该校有九年级学生350人，请估计这些学生中选“跳绳”的约有多少人？

(3)、在调查中选报“铅球”的4名学生，其中有3名男生，1名女生．为了了解学生的训练效果，从这4名学生中随机抽取两名学生进行“铅球”选项测试，请用列举法求所抽取的两名学生中恰好有1名男生和1名女生的概率．

查看试题解析
22. 已知反比例函数y $= \frac{m - 2}{x}$ 的图象与正比例函数y＝﹣3x的图象交于点A（2，﹣6）和点B（n，6）．

(1)、求m和n的值．

(2)、请直接写出不等式 $\frac{m - 2}{x} ＜ -$ 3x的解集．

(3)、将正比例函数y＝﹣3x图象向上平移9个单位后，与反比例函数y $= \frac{m - 2}{x}$ 的图象交于点C和点D．求△COD的面积．

查看试题解析
23. 如图，在△ABC中，∠ABC＝90°，过点B作BD⊥AC于点D．

(1)、尺规作图，作边BC的垂直平分线，交边AC于点E．

(2)、若AD：BD＝3：4，求sinC的值．

(3)、已知BC＝10，BD＝6．若点P为平面内任意一动点，且保持∠BPC＝90°，求线段AP的最大值．

查看试题解析
24. 在平面直角坐标系xOy中，二次函数 $y = a x^{2} + b x + 4$ （a＜0）的图象与x轴交于点A（﹣2，0）和点B（4，0），与y轴交于点C，直线BC与对称轴交于点D．

(1)、求二次函数的解析式．

(2)、若抛物线 $y = a x^{2} + b x + 4$ （a＜0）的对称轴上有一点M，以O、C、D、M四点为顶点的四边形是平行四边形时，求点M的坐标．

(3)、将抛物线 $y = a x^{2} + b x + 4$ （a＜0）向右平移2个单位得到新抛物线，新抛物线与原抛物线交于点E，点F是新抛物线的对称轴上的一点，点G是坐标平面内一点，当以D、E、F、G四点为顶点的四边形是菱形时，求点F的坐标．

查看试题解析
25. 如图1，在正方形ABCD中，E为边AD上的一点，连结CE，过D作DF⊥CE于点G，DF交边AB于点F．已知DG＝4，CG＝16．

(1)、EG的长度是．

(2)、如图2，以G为圆心，GD为半径的圆与线段DF、CE分别交于M、N两点．
①连接CM、BM，若点P为BM的中点，连结CP，求证∠BCP＝∠MCP．
②连接CN、BN，若点Q为BN的中点，连结CQ，求线段CQ的长．

查看试题解析

自选项目	立定跳远	三级蛙跳	跳绳	实心球	铅球
人数/人	9	13	8	b	4
频率	a	0.26	0.16	0.32	0.08