广东省广州市花都区2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下面四个实数,你认为是无理数的是( )A、 B、 C、3 D、0.32. 甲、乙两位学生各进行5次一分钟跳绳训练,经统计两人的平均成绩相同,方差分别为 , , 则成绩更为稳定的是( )A、甲 B、乙 C、甲、乙成绩一样稳定 D、无法确定3. (﹣1,2)关于原点对称的点的坐标为( )A、(﹣1,﹣2) B、(1,2) C、(﹣1,2) D、(1,﹣2)4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,A,B,C是⊙O上的三点,∠OAB=20°,则∠C的度数是( )
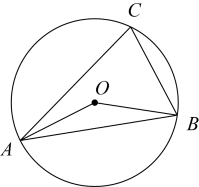 A、40° B、70° C、110° D、140°6. 甲、乙两位同学去图书馆参加整理书籍的志愿活动,已知甲每小时比乙多整理5本,甲整理80本书所用的时间与乙整理70本书所用的时间相同,设乙每小时整理x本书,根据题意列方程得( )A、 B、 C、 D、7. 函数与在同一直角坐标系中的大致图象可能是( )A、
A、40° B、70° C、110° D、140°6. 甲、乙两位同学去图书馆参加整理书籍的志愿活动,已知甲每小时比乙多整理5本,甲整理80本书所用的时间与乙整理70本书所用的时间相同,设乙每小时整理x本书,根据题意列方程得( )A、 B、 C、 D、7. 函数与在同一直角坐标系中的大致图象可能是( )A、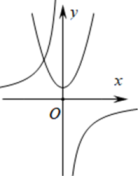 B、
B、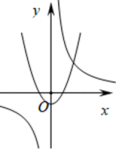 C、
C、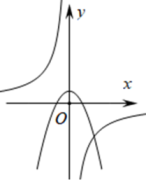 D、
D、 8. 已知a,b,4是等腰三角形的三边长,且a,b是关于x的方程的两个实数根,则m的值是( )A、 B、 C、或 D、或9. 如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,则∠BAD的正弦值为( )
8. 已知a,b,4是等腰三角形的三边长,且a,b是关于x的方程的两个实数根,则m的值是( )A、 B、 C、或 D、或9. 如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,则∠BAD的正弦值为( ) A、 B、 C、 D、10. 已知,直线l:与x轴交于点A,点B与点A关于y轴对称.M是直线l上的动点,将OM绕点O逆时针旋转60°得ON.连接BN,则线段BN的最小值为( )
A、 B、 C、 D、10. 已知,直线l:与x轴交于点A,点B与点A关于y轴对称.M是直线l上的动点,将OM绕点O逆时针旋转60°得ON.连接BN,则线段BN的最小值为( )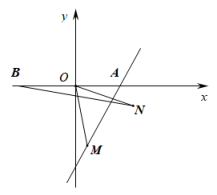 A、 B、3 C、 D、
A、 B、3 C、 D、二、填空题
-
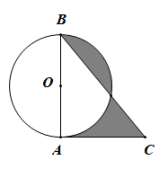
11. 若点O是直线AB上一点,OC是一条射线,当∠AOC=50°时,则∠BOC的度数是 .12. 计算 =13. 已知直线与直线交于点(2,4),则关于x,y的方程组的解是 .14. 若关于x的方程的解为负数,则点(m,m+2)在第象限.15. 如图,AB是⊙O的直径,AC是⊙O的切线,且AB=AC=4,则图中阴影部分的面积为 .
三、解答题
-
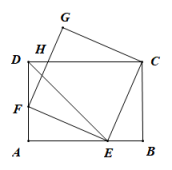
16. 如图,在矩形ABCD中,DE平分∠ADC,交AB于点E,EF⊥CE交AD于点F,以CE,EF为边,作矩形CEFG,FG与DC相交于点H.则下列结论:①AE=BC;②若AE=4,CH=5,则CE=;③EF=AE+DH;④当F是AD的中点时, . 其中正确的结论是(填写所有正确结论的序号).
 17. 解不等式组:18. 如图,点C是AB的中点,DA⊥AB,EB⊥AB,AD=BE.求证:DC=EC.
17. 解不等式组:18. 如图,点C是AB的中点,DA⊥AB,EB⊥AB,AD=BE.求证:DC=EC. 19. 已知 .(1)、化简P;(2)、若 , 求P的值.20. 为了落实“双减”政策,更好地进行家校共育,学校计划对每位学生进行家访,家访的形式由家长自行选择,某班主任对本班学生家长的家访形式进行调查统计,并绘制如下的统计表和不完整的扇形统计图.
19. 已知 .(1)、化简P;(2)、若 , 求P的值.20. 为了落实“双减”政策,更好地进行家校共育,学校计划对每位学生进行家访,家访的形式由家长自行选择,某班主任对本班学生家长的家访形式进行调查统计,并绘制如下的统计表和不完整的扇形统计图.家访形式
数量(人)
入户家访
4
电话家访
15
短信家访
16
到校家访
10
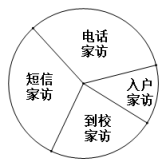 (1)、扇形统计图中,“电话家访”所占圆心角的度数是 .(2)、若选择“入户家访”的四位学生分别为A,B,C,D班主任决定本周从这四人中随机选取两人进行入户家访,用列表法或画树状图法求恰好选中A,B两人的概率.21. 学校玩转数学小组利用无人机测量大树BC的高,当无人机在A处时,恰好测得大树顶端C的俯角为45°,大树底端B的俯角为60°,此时无人机距离地面的高度AD=30米,求大树BC的高.(结果保留小数点后一位. , )
(1)、扇形统计图中,“电话家访”所占圆心角的度数是 .(2)、若选择“入户家访”的四位学生分别为A,B,C,D班主任决定本周从这四人中随机选取两人进行入户家访,用列表法或画树状图法求恰好选中A,B两人的概率.21. 学校玩转数学小组利用无人机测量大树BC的高,当无人机在A处时,恰好测得大树顶端C的俯角为45°,大树底端B的俯角为60°,此时无人机距离地面的高度AD=30米,求大树BC的高.(结果保留小数点后一位. , ) 22. 如图,在△ABC中,AB=9,BC=6.
22. 如图,在△ABC中,AB=9,BC=6. (1)、在AB上求作点E,使得EA=EC;(不写作法,保留作图痕迹)(2)、若∠ACB=2∠A,求AE的长.23. 如图,反比例函数经过点M(a,b),其中a,b满足 .
(1)、在AB上求作点E,使得EA=EC;(不写作法,保留作图痕迹)(2)、若∠ACB=2∠A,求AE的长.23. 如图,反比例函数经过点M(a,b),其中a,b满足 .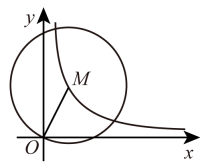 (1)、求反比例函数的解析式;(2)、以点M为圆心,MO为半径画圆,点N圆周上一点,∠OMN=120°,求点N的坐标.24. 如图,在△ABC中,CD平分∠ACB,且AD=BD.
(1)、求反比例函数的解析式;(2)、以点M为圆心,MO为半径画圆,点N圆周上一点,∠OMN=120°,求点N的坐标.24. 如图,在△ABC中,CD平分∠ACB,且AD=BD. (1)、若AC=6,BC=8,AB=10,求∠ACD的度数;(2)、证明:∠ACB+∠ADB=180°;(3)、设 , 试判断CA,CD,CB之间的数量关系(用含k的式子表示),并说明理由.25. 已知抛物线与x轴交于A,B两点(A在B的左侧),点C(4,5).(1)、判断点C(4,5)是否在抛物线上;(2)、直线AC与抛物线的对称轴交于点D,连接BC,BD.
(1)、若AC=6,BC=8,AB=10,求∠ACD的度数;(2)、证明:∠ACB+∠ADB=180°;(3)、设 , 试判断CA,CD,CB之间的数量关系(用含k的式子表示),并说明理由.25. 已知抛物线与x轴交于A,B两点(A在B的左侧),点C(4,5).(1)、判断点C(4,5)是否在抛物线上;(2)、直线AC与抛物线的对称轴交于点D,连接BC,BD.①若 , 求抛物线的解析式;
②将直线AC沿x轴翻折所得直线与抛物线的另一个交点为E,F是线段AE上的一点,且EF=3AF.P是△ABC的外心,设过点P,F的直线l与x轴的夹角为α(0°<α<90°).试判断α的大小是否发生变化,若不变,请求出tan α值;若发生变化,请说明理由.