广东省广州市海珠区2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列各数中,无理数是( )A、 B、 C、3 D、2. 下列图形中,中心对称图形是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知一组数据:12、17、13、11、15,这组数据的中位数是( )A、13 B、14 C、15 D、174. 下列计算中,正确的是( )A、 B、 C、 D、5. 如图,△ABC中,∠ABC=90°沿BC所在的直线向右平移得到△DEF,下列结论中不一定成立的是( )
3. 已知一组数据:12、17、13、11、15,这组数据的中位数是( )A、13 B、14 C、15 D、174. 下列计算中,正确的是( )A、 B、 C、 D、5. 如图,△ABC中,∠ABC=90°沿BC所在的直线向右平移得到△DEF,下列结论中不一定成立的是( ) A、EC=CF B、∠DEF=90° C、AC=DF D、ACDF6. 如图,平行四边形ABCD的周长是32,对角线AC、BD相交于点O,点E是AD的中点,BD=12,则△DOE的周长为( )
A、EC=CF B、∠DEF=90° C、AC=DF D、ACDF6. 如图,平行四边形ABCD的周长是32,对角线AC、BD相交于点O,点E是AD的中点,BD=12,则△DOE的周长为( ) A、16 B、14 C、22 D、187. 如图,在⊙O中,AO=3,∠C=60°,则劣弧的长度为( )
A、16 B、14 C、22 D、187. 如图,在⊙O中,AO=3,∠C=60°,则劣弧的长度为( ) A、6π B、9π C、2π D、3π8. 某小区原有一块长为30米,宽为20米的矩形康乐健身区域,现计划在这一场地四周(场内)筑一条宽度相等的健走步道,其步道面积为214平方米,设这条步道的宽度为x米,可以列出方程是( )
A、6π B、9π C、2π D、3π8. 某小区原有一块长为30米,宽为20米的矩形康乐健身区域,现计划在这一场地四周(场内)筑一条宽度相等的健走步道,其步道面积为214平方米,设这条步道的宽度为x米,可以列出方程是( )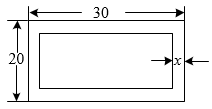 A、 B、 C、 D、9.
A、 B、 C、 D、9.如图,A、B是双曲线上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为( )
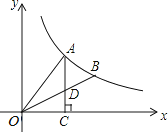 A、 B、 C、3 D、410. 若二次函数 , 当时, , 则a的值是( )A、1 B、 C、 D、﹣1
A、 B、 C、3 D、410. 若二次函数 , 当时, , 则a的值是( )A、1 B、 C、 D、﹣1二、填空题
-
11. 若分式 的值等于1,则x= .12. 二次函数的图象的顶点坐标是 .13. 若圆锥的母线长为4,底面半径为3,则该圆锥的侧面积是 .14. 若 ,则 的取值范围是 .15. 菱形的两个内角的度数比是1:3,一边上的高长是4,则菱形的面积是 .16. 图,在⊙O中,AC,BD是直径,∠BOC=60°,点P是劣弧AB上任意一点(不与A、B重合),过点P作AC垂线,交AC、BD所在直线于点E,F,过点P作BD垂线,交BD、AC所在直线于点G、H,下列选项中,正确的是 .
①;②∠GPE=60°;③PG+PE最大值为;④当△PEH≌△CBA时, .

三、解答题
-
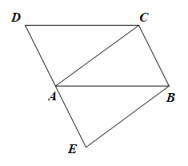
17. 解不等式组:18. 如图,已知点E在平行四边形ABCD边DA延长线上,且AE=AD.求证:四边形AEBC是平行四边形.
 19. 已知 .(1)、化简T;(2)、若a、b是方程的两个根,求T的值.20. 2022春开学,为防控新冠病毒,学生进校必须戴口罩,测体温,某校开通了A、B、C三条人工测体温的通道,在三个通道中,可随机选择其中的一个通过.(1)、其中一个学生进校园时,由A通道过的概率是;(2)、求两学生进校园时,都是C通道过的概率.(用画“树状图”或“列表格”)21. 某地为了让山顶通电,需要从山脚点B开始接驳电线,经过中转站D,再连通到山顶点A处,测得山顶A的高度AC为300米,从山脚B到山顶A的水平距离BC是500米,斜面BD的坡度i=1:2(指DF与BF的比),从点D看向点A的仰角为45°.
19. 已知 .(1)、化简T;(2)、若a、b是方程的两个根,求T的值.20. 2022春开学,为防控新冠病毒,学生进校必须戴口罩,测体温,某校开通了A、B、C三条人工测体温的通道,在三个通道中,可随机选择其中的一个通过.(1)、其中一个学生进校园时,由A通道过的概率是;(2)、求两学生进校园时,都是C通道过的概率.(用画“树状图”或“列表格”)21. 某地为了让山顶通电,需要从山脚点B开始接驳电线,经过中转站D,再连通到山顶点A处,测得山顶A的高度AC为300米,从山脚B到山顶A的水平距离BC是500米,斜面BD的坡度i=1:2(指DF与BF的比),从点D看向点A的仰角为45°. (1)、斜面AD的坡度i=;(2)、求电线AD+BD的长度(结果保留根号).22. 一次函数的图象与反比例函数的图象相交于 , 两点.
(1)、斜面AD的坡度i=;(2)、求电线AD+BD的长度(结果保留根号).22. 一次函数的图象与反比例函数的图象相交于 , 两点. (1)、求反比例函数的解析式;(2)、以直线x=2为对称轴,作直线的轴对称图形,交x轴于点C,连接AC,求AC的长度.23. 在Rt△ACB中,∠ACB=90°,以AC长为半径作⊙A.
(1)、求反比例函数的解析式;(2)、以直线x=2为对称轴,作直线的轴对称图形,交x轴于点C,连接AC,求AC的长度.23. 在Rt△ACB中,∠ACB=90°,以AC长为半径作⊙A. (1)、尺规作图:将△ACB绕点A顺时针旋转得△AC'B',使得点C的对应点C'落在线段AB上(保留作图痕迹,不用写画法);(2)、在(1)的条件下,若线段B'A与⊙A交于点P,连接BP.
(1)、尺规作图:将△ACB绕点A顺时针旋转得△AC'B',使得点C的对应点C'落在线段AB上(保留作图痕迹,不用写画法);(2)、在(1)的条件下,若线段B'A与⊙A交于点P,连接BP.①求证:BP与⊙A相切;
②如果CA=5,CB=12,BP与B'C'交于点O,连接OA,求OA的长.
24. 如图,AC、BD为⊙O的直径,且AC⊥BD,P、Q分别为半径OB、OA(不与端点重合)上的动点,直线PQ交⊙O于M、N. (1)、比较大小:cos∠OPQsin∠OQP;(2)、请你判断与OP·cos∠OPQ之间的数量关系,并给出证明;(3)、当∠APO=60°时,设MQ=m·MP,NQ=n·NP.
(1)、比较大小:cos∠OPQsin∠OQP;(2)、请你判断与OP·cos∠OPQ之间的数量关系,并给出证明;(3)、当∠APO=60°时,设MQ=m·MP,NQ=n·NP.①求m+n的值;
②以OD为边在OD上方构造矩形ODKS,已知OD=1,OS= , 在Q点的移动过程中,恒为非负数,请直接写出实数c的最大值.
25. 已知抛物线与x轴交于A(﹣2,0)和B(2,0).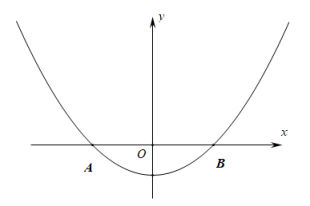 (1)、求抛物线的解析式;(2)、取抛物线上异于A、B的一个动点C,作C关于x轴的对称点 , 直线交抛物线于点D.
(1)、求抛物线的解析式;(2)、取抛物线上异于A、B的一个动点C,作C关于x轴的对称点 , 直线交抛物线于点D.①记直线CD与x轴的夹角为α(α<90°),求α;
②如果△ADC覆盖的区域内的点一定分布在四个象限内,且△ADC内角中有一个钝角β满足105°<β<135°,求点C横坐标的取值范围.