广东省广州市白云区2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 计算:( )A、-2 B、-1 C、1 D、22. 若a与b互为相反数,则( )A、 B、 C、 D、3. 方程的解为( )A、 , B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列命题的逆命题中,是假命题的是( )A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、对角线互相垂直的四边形是矩形 D、有一个角是直角的四边形是矩形6. 有4张分别印有实数0,-0.5, , -2的纸牌,除数字外无其他差异。从这4张纸牌中随机抽取2张,恰好抽到2张均印有负数的纸牌的概率为( ).A、 B、 C、 D、7. 如图,的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,已知的周长为36. , , 则AF的长为( )
 A、4 B、5 C、9 D、138. 抛物线经过点 , , , 则当时,y的值为( ).A、6 B、1 C、-1 D、-69. 如图,在中, , , , 作等腰三角形ABD,使 . , 且点C不在射线AD上.过点D作 , 垂足为E.则的值为( ).
A、4 B、5 C、9 D、138. 抛物线经过点 , , , 则当时,y的值为( ).A、6 B、1 C、-1 D、-69. 如图,在中, , , , 作等腰三角形ABD,使 . , 且点C不在射线AD上.过点D作 , 垂足为E.则的值为( ).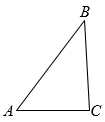 A、 B、 C、 D、10. 在平面直角坐标系xOy中,矩形ABCO的点A在函数的图象上,点C在函数的图象上,若点B的纵坐标为3,则符合条件的所有点A的纵坐标之和为( )A、0 B、1 C、2 D、3
A、 B、 C、 D、10. 在平面直角坐标系xOy中,矩形ABCO的点A在函数的图象上,点C在函数的图象上,若点B的纵坐标为3,则符合条件的所有点A的纵坐标之和为( )A、0 B、1 C、2 D、3二、填空题
-
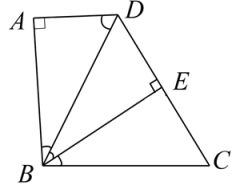
11. 当x满足条件时,式子在实数范围内有意义.12. 方程的解为 .13. 如图,在四边形ABCD中,AD∥BC, , , BE垂直平分CD,交CD于点E,若 , 则CE的长为 .
 14. 点A是反比例函数上的点,过点A作轴,垂足为B.若的面积为8,则一元二次方程的根的情况为 .15. 如图,在关于x的方程(a,b为常数)中,x的值可以理解为:在数轴上,到A点的距离等于b的点X对应的数.例如:因为到实数1对应的点A距离为3的点X对应的数为4和-2,所以方程的解为 , . 用上述理解,可得方程的解为 .
14. 点A是反比例函数上的点,过点A作轴,垂足为B.若的面积为8,则一元二次方程的根的情况为 .15. 如图,在关于x的方程(a,b为常数)中,x的值可以理解为:在数轴上,到A点的距离等于b的点X对应的数.例如:因为到实数1对应的点A距离为3的点X对应的数为4和-2,所以方程的解为 , . 用上述理解,可得方程的解为 . 16. 如图,正方形ABCD中,分别以B,D为圆心,以正方形的边长10为半径画弧,形成树叶型(阴影部分)图案.
16. 如图,正方形ABCD中,分别以B,D为圆心,以正方形的边长10为半径画弧,形成树叶型(阴影部分)图案.
①树叶图案的周长为;
②树叶图案的面积为;
③若用扇形BAC围成圆锥,则这个圆锥底面半径为2.5;
④若用扇形BAC围成圆锥,则这个圆锥的高为;上述结论正确的有 .
三、解答题
-
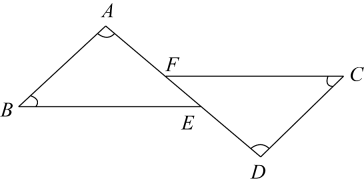
17. 解不等式组:并将其解集在数轴上表示出来.18. 如图,点E,F在线段AD上,AB∥CD, , . 求证: .
 19. 已知 .(1)、化简M;(2)、若 , 求M的值.20. 下表记录了一名球员在罚球线上投篮的结果.
19. 已知 .(1)、化简M;(2)、若 , 求M的值.20. 下表记录了一名球员在罚球线上投篮的结果.投篮次数n
10
10
10
10
10
150
300
500
投中次数m
3
6
5
6
7
78
152
251
(1)、在这个记录表中,投篮次数为10次时,投中次数的众数是 , 中位数是;(2)、在这个记录表中,投篮次数为500次时,投中的频率是;(3)、这名球员投篮一次,投中的概率约是多少?21. 老张与老李购买了相同数量的种兔.(1)、一年后,老张养兔数比买入种兔数增加了2只,老李养兔数比买入种兔数的2倍少1只,老张养兔数不超过老李养兔数的 . 一年前老张至少买了多少只种兔?(2)、两年后,老张的养兔数比买入种兔数增加了69%.若这两年兔子数目的增长率不变,则每年的增长率为多少?22. 如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD. (1)、判断直线PD与⊙O的位置关系,并加以证明;(2)、联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC= , 求EG的长.23. 如图,在四边形ABCD中, , CF∥AD, , , E是AF的中点,CE平分 .
(1)、判断直线PD与⊙O的位置关系,并加以证明;(2)、联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC= , 求EG的长.23. 如图,在四边形ABCD中, , CF∥AD, , , E是AF的中点,CE平分 .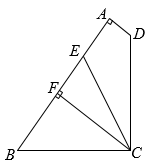 (1)、求证:;(2)、若 , 求 .24. 如图,矩形ABCD中AB=10,AD=6,点E为AB边上的动点(不与A,B重合),把△ADE沿DE翻折,点A的对应点为G,延长EG交直线DC于点F,再把△BEH沿EH翻折,使点B的对应点T落在EF上,折痕EH交直线BC于点H.
(1)、求证:;(2)、若 , 求 .24. 如图,矩形ABCD中AB=10,AD=6,点E为AB边上的动点(不与A,B重合),把△ADE沿DE翻折,点A的对应点为G,延长EG交直线DC于点F,再把△BEH沿EH翻折,使点B的对应点T落在EF上,折痕EH交直线BC于点H. (1)、求证:△GDE∽△TEH;(2)、若点G落在矩形ABCD的对称轴上,求AE的长;(3)、是否存在点T落在DC边上?若存在,求出此时AE的长度,若不存在,请说明理由.25. 已知抛物线y=ax2+bx−(a>0)与x轴交于点A,B两点,OA<OB,AB=4.其顶点C的横坐标为-1.(1)、求该抛物线的解析式;(2)、设点D在抛物线第一象限的图象上,垂足为E,DF∥y轴交直线AC于点F,当面积等于4时,求点D的坐标;(3)、在(2)的条件下,点M是抛物线上的一点,M点从点B运动到达点C,交直线BD于点N,延长MF与线段DE的延长线交于点H,点P为N,F,H三点构成的三角形的外心,求点P经过的路线长.
(1)、求证:△GDE∽△TEH;(2)、若点G落在矩形ABCD的对称轴上,求AE的长;(3)、是否存在点T落在DC边上?若存在,求出此时AE的长度,若不存在,请说明理由.25. 已知抛物线y=ax2+bx−(a>0)与x轴交于点A,B两点,OA<OB,AB=4.其顶点C的横坐标为-1.(1)、求该抛物线的解析式;(2)、设点D在抛物线第一象限的图象上,垂足为E,DF∥y轴交直线AC于点F,当面积等于4时,求点D的坐标;(3)、在(2)的条件下,点M是抛物线上的一点,M点从点B运动到达点C,交直线BD于点N,延长MF与线段DE的延长线交于点H,点P为N,F,H三点构成的三角形的外心,求点P经过的路线长.