广东省佛山市南海区2022年中考二模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. -2022的绝对值是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 滴水的质量约0.000 051 2kg，这个数据用科学记数法表示为（）

A、0.512× $1 0^{- 8}$ B、5.12× $1 0^{- 7}$ C、512× $1 0^{- 5}$ D、5.12× $1 0^{- 5}$

查看试题解析
3. 一个袋中装有20个球，其中有5个黑球和15个白球，每个球除颜色外都相同，从中任意摸出一个球是白球的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{3}{4}$ D、1

查看试题解析
4. 一个几何体由若干大小相同的小立方木块搭成，如图是它的主视图和俯视图，那么搭成该几何体所需小立方木块的个数最少为（）

A、3 B、4 C、5 D、6

查看试题解析
5. 某班为了解学生每周“家务劳动”情况，随机调查了7名学生每周的劳动时间，一周内累计参加家务劳动的时间分别为：2小时、3小时、2小时、3小时、2.5小时、3小时、1.5小时，则这组数据的中位数为（）

A、1.5小时 B、2小时 C、2.5小时 D、3小时

查看试题解析
6. 如图，E、F是正方形ABCD的对角线BD上的两点，BD=10，DE=BF=2，则四边形AECF的周长等于（）

A、20 B、 $20 \sqrt{2}$ C、30 D、 $4 \sqrt{34}$

查看试题解析
7. 观察用直尺和圆规作一个角等于已知角的示意图，能得出∠CPD=∠AOB的依据是（）

A、由“等边对等角”可得∠CPD=∠AOB B、由SSS可得△OGH≌△PMN，进而可证∠CPD $=$ ∠AOB C、由SAS可得△OGH≌△PMN，进而可证∠CPD $=$ ∠AOB D、由ASA可得△OGH≌△PMN，进而可证∠CPD $=$ ∠AOB

查看试题解析
8. 若一次函数y $=$ kx＋b的图象过点（-2，0）、（0，1），则不等式 $k (x - 1) + b$ ＞0的解集是（）

A、x＞ $- 2$ B、x＞ $- 1$ C、x＞1 D、x＞2

查看试题解析
9. 若a、b是关于x的一元二次方程x² $- 2$ kx＋4k $=$ 0的两个实数根，且a²＋b²＝12，则k的值是（）

A、-1 B、3 C、-1或3 D、-3或1

查看试题解析
10. 如图，抛物线y $=$ ax²＋bx＋c（a＞0）与x轴交于A（ $- 3$ ， 0）、B两点，与y轴交于点C，点（m $- 5$ ， n）与点（3 $- m$ ， n）也在该抛物线上．下列结论：①点B的坐标为（1，0）；②方程ax²＋bx＋c $-$ 2 $=$ 0有两个不相等的实数根；③ $\frac{5}{4}$ a＋c＜0；④当x $=$ $-$ t² $- 2$ 时，y＞c．正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 15的算术平方根是．

查看试题解析
12. 若一个正n边形的一个内角与和它相邻的外角的度数之比是3：1，那么n= ．

查看试题解析
13. 已知a、b、c都是实数，若 $\sqrt{a - 2} + | 2 b + \frac{1}{2} | + {(c + 2 a)}^{2} = 0$ ，则 $\frac{a - c}{4 a + 8 b}$ $=$ ．

查看试题解析
14. 已知 $x + y = - 6$ ， $x y = \frac{1}{4}$ ，则 $x^{3} y + 2 x^{2} y^{2} + x y^{3}$ 的值为．

查看试题解析
15. 如图，等边△OAB的边长为4，则点A的坐标为．

查看试题解析
16. 如图，四边形ABCD是正方形，曲线DA₁B₁C₁D₁A₂B₂…叫做“正方形的渐开线”，其中 $\overset{⌢}{D A_{1}}$ 的圆心为点A，半径为AD； $\overset{⌢}{A_{1} B_{1}}$ 的圆心为点B，半径为BA₁； $\overset{⌢}{B_{1} C_{1}}$ 的圆心为点C，半径为CB₁； $\overset{⌢}{C_{1} D_{1}}$ 的圆心为点D，半径为DC₁；…， $\overset{⌢}{D A_{1}}$ 、 $\overset{⌢}{A_{1} B_{1}}$ 、 $\overset{⌢}{B_{1} C_{1}}$ 、 $\overset{⌢}{C_{1} D_{1}}$ 、…的圆心依次按A、B、C、D循环．当 $A B = 1$ 时，则 $\overset{⌢}{A_{2022} B_{2022}}$ 的长是．

查看试题解析
17. 如图，在△ABC中，AB $=$ CB $=$ 9，∠B $=$ 90°，点O是△ABC内一点，过点O分别作边 AB、BC的垂线，垂足分别为点D、E，且OD²＋OE² $=$ 36，连接OA、OC，则△AOC面积的最小值为．

查看试题解析

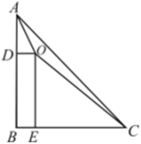
三、解答题

18. 解不等式组： ${\begin{array}{l} 5 x - 3 \leq 2 x ， ① \\ \frac{x - 1}{4} ＜ \frac{x + 3}{2} - 1 . ② \end{array}$

查看试题解析
19. 2021年全国居民人均消费支出构成情况如下面的图表所示．
表1：2021年全国居民人均消费支出构成情况
种类
饮食
衣着
居住
生活用品
交通通信
教育文娱
医疗
其他
消费（元）
a
1600
5600
1500
3200
2400
2100
600
2021年全国居民人均消费支出构成情况 2021年全国居民人均消费支出构成情况
请根据其中的信息回答以下问题：

(1)、2021年全国居民人均总支出为元，图2中其他支出所对应扇形的圆心角的度数为．

(2)、请将图1补充完整．

(3)、小明家2021年人均消费总支出为3万元，请你估计小明家2021年的人均饮食支出约为多少元？

查看试题解析
20. 北京冬奥会的吉祥物冰墩墩深受大家喜爱，出现“一墩难求”的现象．负责生产冰墩墩硅胶外壳的公司收到了一笔48万个的订单，若按原计划生产的日产量计算，则完成这笔订单的生产时间将超过一年．扩大生产规模后，日产量可提高到原来的30倍，生产时间能减少464天．

(1)、扩大生产规模后每天生产多少个冰墩墩硅胶外壳？

(2)、该公司通过增加模具的方式提高日产量，本来只有两套模具，每套模具每天平均生产500个冰墩墩硅胶外壳，为达到扩大生产规模后的日产量，至少需要增加多少套模具？

查看试题解析
21. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 的垂直平分线分别交 $B C$ 、 $A D$ 于点 $E$ 、 $F$ ，连接 $A E$ 、 $C F$ ．

(1)、求证：四边形 $A E C F$ 是菱形．

(2)、当AB $=$ 4，BC $=$ 8时，求线段EF的长．

查看试题解析
22. 已知一次函数y $=$ 3x＋b的图象与反比例函数y $=$ $\frac{k}{x}$ (x＞0)的图象交于点A(m，3)，与x轴交于点B，△AOB的面积为3．

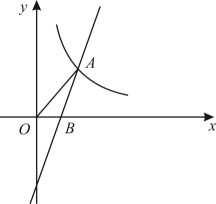(1)、求一次函数和反比例函数的表达式．

(2)、根据图象直接回答，在第一象限内，当x取何值时，一次函数的值大于反比例函数的值？

(3)、点C为x轴上一点，若△COA与△AOB相似，求AC的长．

查看试题解析
23. 如图1，⊙O的直径为BC，点A在⊙O上，∠BAC的平分线AD与BC交于点E，与⊙O交于点D， $A B = 2$ ， $B D = 2 \sqrt{2}$ ．

(1)、求 $t a n ∠ A D B$ ．

(2)、求证： $A B + A C = \sqrt{2} A D$ ．

(3)、如图2，点F是AB延长线上一点，且 $C D \cdot D E = B F \cdot C E$ ．求证：DF是⊙O的切线，并求线段DF的长．

查看试题解析
24. 已知二次函数y $=$ x²＋bx＋c的图象与x轴交于A（1，0）和B（-3，0），与y轴交于点C．

(1)、求该二次函数的表达式．

(2)、如图1，连接BC，动点D以每秒1个单位长度的速度由A向B运动，同时动点E以每秒 $\sqrt{2}$ 个单位长度的速度由B向C运动，连接DE，当点E到达点C的位置时，D、E同时停止运动，设运动时间为t秒．当△BDE为直角三角形时，求t的值．

(3)、如图2，在抛物线对称轴上是否存在一点Q，使得点Q到x轴的距离与到直线AC的距离相等，若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

种类	饮食	衣着	居住	生活用品	交通通信	教育文娱	医疗	其他
消费（元）	a	1600	5600	1500	3200	2400	2100	600