山东省淄博市淄川区2022年中考一模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 北京时间2021年10月16日0时23分，搭载神舟十三号载人飞船的长征二号 $F$ 遥十三运载火箭，在酒泉卫星发射中心按照预定时间精准点火发射，约582秒后，神舟十三号载人飞船与火箭或功分离，进入预定轨道，顺利将翟志刚、王亚平、叶光富3名航天员送入太空，飞行约18.2万千米后对接于天和核心舱节点舱面向地球一侧的径向对接口．其中18.2万用科学记数法表示为（）

A、 $1.82 \times 1 0^{5}$ B、 $18.2 \times 1 0^{5}$ C、 $18.2 \times 1 0^{4}$ D、 $0.182 \times 1 0^{6}$

查看试题解析
2. 下列图形：

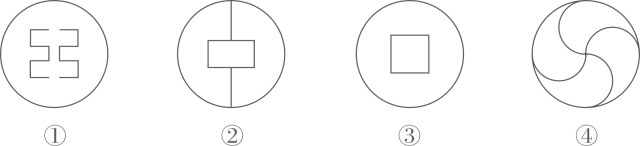
其中是轴对称图形且有两条对称轴的是（）

A、①② B、②③ C、②④ D、③④

查看试题解析
3. 已知三角形的三边长分别为3，4，x，且x为整数，则x的最大值为（）

A、8 B、7 C、5 D、6

查看试题解析
4. 祖冲之是中国数学史上第一个名列正史的数学家，他把圆周率精确到小数点后7位，这是祖冲之最重要的数学贡献．数学活动课上，孙老师对圆周率的小数点后100位数字进行了统计：
数字
0
1
2
3
4
5
6
7
8
9
频数
8
8
12
11
10
8
9
8
12
14
那么，圆周率的小数点后100位数字的众数与中位数分别为（）

A、14，5 B、5，9 C、9，5 D、14，4.5

查看试题解析
5.
如图是由6个相同的小立方块搭成的几何体，则下列说法正确的是（　　）

A、主视图的面积最大 B、俯视图的面积最大 C、左视图的面积最大 D、三个视图面积一样大

查看试题解析
6. 当x＝2时，代数式 $a x^{5} + b x^{3} + c x - 7$ 的值是-10，则当x＝-2时，该代数式的值为（）

A、-10 B、10 C、4 D、-4

查看试题解析
7. 下列一元二次方程中，有两个相等实数根的是（）

A、 $x^{2} + x = 0$ B、 $x^{2} + 1 = 0$ C、 $(x - 1)^{2} = 4$ D、 $x^{2} - 6 x + 9 = 0$

查看试题解析
8. 已知点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ 都在反比例函数 $y = - \frac{5}{x}$ 的图象上，并且 $y_{1} < y_{2} < 0 < y_{3}$ ，则下列结论正确的是（）

A、 $x_{2} < x_{1} < x_{3}$ B、 $x_{1} < x_{2} < x_{3}$ C、 $x_{3} < x_{1} < x_{2}$ D、 $x_{2} < x_{3} < x_{1}$

查看试题解析
9. 关于x的分式方程 $\frac{m}{x + 6} = 1$ ，下列说法正确的是（）

A、方程的解是x＝m－6 B、当m＜6时，方程的解是负数 C、当m＞6时，方程的解是正数 D、以上说法均不符合题意

查看试题解析
10. 如图，在边长为 $2 \sqrt{2}$ 的正方形ABCD中，E，F分别是边AB，BC的中点，连接CE，DF，G，H分别是CE，DF的中点，连接GH，则GH的长为（）

A、 $\sqrt{2}$ B、1 C、2 D、 $\frac{\sqrt{2}}{2}$

查看试题解析
11. 直角坐标系中，若干个半径为1个单位长度，圆心角为60°的扇形组成一条连续的曲线（如图），点P从原点O出发，沿这条曲线向右上下起伏运动，点P在直线上的速度为1个单位长度/秒，在曲线上的速度为 $\frac{π}{3}$ 个单位长度/秒，则2022秒时，点P的坐标为（）

A、 $(2022 ， \sqrt{3})$ B、（1011，0） C、 $(1011 ， - \frac{\sqrt{3}}{2})$ D、（2022，0）

查看试题解析
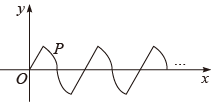12. 如图①，E为矩形ABCD的边AD上一点，点P从点B出发沿折线B﹣E﹣D运动到点D停止，点Q从点B出发沿BC运动到点C停止，它们的运动速度都是1cm/s.现P，Q两点同时出发，设运动时间为x（s），△BPQ的面积为y（cm²），若y与x的对应关系如图②所示，则矩形ABCD的面积是（）

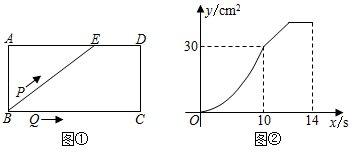A、96cm² B、84cm² C、72cm² D、56cm²

查看试题解析

二、填空题

13. $s i n^{2} 3 0^{°} \div 2^{- 2} =$ ．

查看试题解析
14. 将多项式 $a b (a - b) - a (b - a)^{2}$ 分解因式的结果是．

查看试题解析
15. 观察下列等式： $4 - 2 = 4 \div 2$ ， $\frac{9}{2} - 3 = \frac{9}{2} \div 3$ ， $- \frac{1}{2} - \frac{1}{2} = - \frac{1}{2} \div \frac{1}{2}$ ，请你写出一个满足以上特征的两个数，并写成等式的形式．

查看试题解析
16. 如图，设双曲线 $y = \frac{k}{x} (k > 0)$ 与直线＝交于，两点（点在第三象限），将双曲线在第一象限内的一支沿射线方向平移，使其经过点，将双曲线在第三象限的一支沿射线方向平移，使其经过点，平移后的两条曲线相交于，两点，此时我们称平移后的两条曲线所围部分（阴影部分）为双曲线的“眸”，为双曲线的“眸径”．当k＝6时，“眸径”的长为．

查看试题解析
17. 如图，边长为4的正三角形ABC，点M，N分别是边AB，AC上的动点，连接BN，CM交于点P．若BN＝CM，当点M由点B运动到点A时，点P所经过的路径长为．

查看试题解析

三、解答题

18. 先化简： $\frac{x}{2 x + 3} \div \frac{3}{4 x^{2} - 9} \cdot \frac{1}{2} (1 + \frac{3}{2 x - 3})$ ，若其结果等于 $\frac{2}{3}$ ，试确定x的值．

查看试题解析
19. 如图，AM∥BC ，且AC平分∠BAM ．

(1)、用尺规作∠ABC的平分线BD交AM于点D ，连接CD ．（只保留作图痕迹，不写作法）

(2)、求证：四边形ABCD是菱形．

查看试题解析
20. 2022年2月4日至2月20日北京冬奥会成功举办．如图，AB表示一条跳台滑雪赛道，在点A处测得起点B的仰角为40°，斜坡CD的坡度为i＝1∶2.4，底端点C与顶端点D的距离为26米，参赛运动员们将从点A出发乘车沿水平方向行驶100米到达点C处，再沿斜坡CD行驶至点D处，最后乘垂直于水平方向的电梯达到点B处，求电梯BD的高度．（结果保留一位小数，参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）

查看试题解析
21. 近年来，在习近平总书记“既要金山银山，又要绿水青山”思想的指导下，我国持续的大面积雾霾天气得到了较大改善．为了调查学生对雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了如图所示的不完整的三种统计图表．
对雾霾天气了解程度的统计表
对雾霾天气了解程度
百分比
A．非常了解
$5 %$
B．比较了解
$15 %$
C．基本了解
$45 %$
D．不了解
$n$
请结合统计图表，回答下列问题：

(1)、本次参与调查的学生共有， n=；

(2)、扇形统计图中 $D$ 部分扇形所对应的圆心角是度；

(3)、请补全条形统计图；

(4)、根据调查结果，学校准备开展关于雾霾的知识竞赛，某班要从“非常了解”程度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球分别标上数字1，2，3，4，然后放到一个不透明的袋中充分摇匀，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去，否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．

查看试题解析

22. 某公司招聘外卖送餐员，送餐员的月工资由底薪1000元加上外卖送单补贴

(

送一次外卖称为一单

)

构成，外卖送单补贴的具体方案如下：

外卖送单数量	补贴 $($ 元 $/$ 单 $)$
每月不超过500单	6
超过500单但不超过m单的部分 $(700 \leq m \leq 900)$	8
超过m单的部分	10

(1)、若某“外卖小哥”4月份送餐400单，则他这个月的工资总额为多少元？

(2)、设5月份某“外卖小哥”送餐x单

(x > 500)

，所得工资为y元，求y与x的函数关系式.

(3)、若某“外卖小哥”5月份送餐800单，所得工资为6500元，求m的值.

查看试题解析

2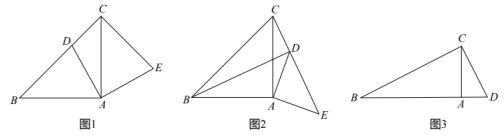3.

(1)、【问题发现】
如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为斜边BC上一点（不与点B，C重合），将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是，位置关系是；

(2)、【探究证明】
如图2，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；

(3)、【拓展延伸】
如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，过点C作CA⊥BD于A．将△ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角∠CAE为 $α$ （0°＜ $α$ ＜360°），当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．

查看试题解析
24. 如图，已知二次函数 $y = a x^{2} + b x - 3$ 的图象与x轴交于点A（－1，0），B（3，0），直线AC与y轴交于点C，与抛物线交于点D，且△ABD的面积为10．

(1)、求抛物线和直线AC的函数表达式；

(2)、若抛物线上的动点E在直线AC的下方，求△ACE面积的最大值，并求出此时点E的坐标；

(3)、设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当△BPQ为等边三角形时，求直线AP的函数表达式．

查看试题解析

对雾霾天气了解程度	百分比
A．非常了解	$5 %$
B．比较了解	$15 %$
C．基本了解	$45 %$
D．不了解	$n$

数字	0	1	2	3	4	5	6	7	8	9
频数	8	8	12	11	10	8	9	8	12	14