山东省淄博市沂源县2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 这四个数中,最小的一个数是( )A、 B、 C、 D、2. 如图是由8个相同的小正方体组成的几何体,其主视图是( )
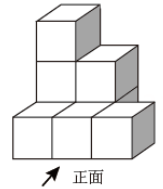 A、
A、 B、
B、 C、
C、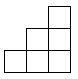 D、
D、 3. 边长是m的正方形面积是7,如图,表示m的点在数轴上位于哪两个字母之间( )
3. 边长是m的正方形面积是7,如图,表示m的点在数轴上位于哪两个字母之间( ) A、C与D B、A与B C、A与C D、B与C4. 某校男子足球队全体队员的年龄分布如表所示.对于这些数据,下列判断正确的是( )
A、C与D B、A与B C、A与C D、B与C4. 某校男子足球队全体队员的年龄分布如表所示.对于这些数据,下列判断正确的是( )年龄(岁)
12
13
14
15
16
人数(人)
2
5
4
7
2
A、中位数14岁,平均年龄14.1岁 B、中位数14.5岁,平均年龄14岁 C、众数14岁,平均年龄14.1岁 D、众数15岁,平均年龄14岁5. 下列计算正确的是( )A、 B、 C、﹣(﹣a)4÷a2=a2 D、6. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD , B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( ) A、四边形ABCD由矩形变为平行四边形 B、BD的长度增大 C、四边形ABCD的面积不变 D、四边形ABCD的周长不变7. 如图,在长形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆住.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
A、四边形ABCD由矩形变为平行四边形 B、BD的长度增大 C、四边形ABCD的面积不变 D、四边形ABCD的周长不变7. 如图,在长形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆住.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的三倍,则称这样的方程为“3倍根方程”,以下说法错误的是( )A、方程x2﹣4x+3=0是3倍根方程 B、若关于x的方程(x﹣3)(mx+n)=0是3倍根方程,则m+n=0 C、若m+n=0且m≠0,则关于x的方程(x﹣3)(mx+n)=0是3倍根方程 D、若3m+n=0且m≠0,则关于x的方程x2+(m﹣n)x﹣mn=0是3倍根方程9. 有A,B两粒质地均匀的正方体骰子(骰子每个面上的点数分别为1,2,3,4,5,6),小王掷A,朝上的数字记作x;小张掷B,朝上的数字记作y.在平面坐标系中有一矩形,四个点的坐标分别为(0,0),(6,0),(6,4)和(0,4),小王小张各掷一次所确定的点P(x,y)落在矩形内(不含矩形的边)的概率是( )A、 B、 C、 D、10. 在使用DY-570型号的计算器时,小明输入一个数据后,按照以下步骤操作,依次按照从第一步到第三步循环按键:
8. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的三倍,则称这样的方程为“3倍根方程”,以下说法错误的是( )A、方程x2﹣4x+3=0是3倍根方程 B、若关于x的方程(x﹣3)(mx+n)=0是3倍根方程,则m+n=0 C、若m+n=0且m≠0,则关于x的方程(x﹣3)(mx+n)=0是3倍根方程 D、若3m+n=0且m≠0,则关于x的方程x2+(m﹣n)x﹣mn=0是3倍根方程9. 有A,B两粒质地均匀的正方体骰子(骰子每个面上的点数分别为1,2,3,4,5,6),小王掷A,朝上的数字记作x;小张掷B,朝上的数字记作y.在平面坐标系中有一矩形,四个点的坐标分别为(0,0),(6,0),(6,4)和(0,4),小王小张各掷一次所确定的点P(x,y)落在矩形内(不含矩形的边)的概率是( )A、 B、 C、 D、10. 在使用DY-570型号的计算器时,小明输入一个数据后,按照以下步骤操作,依次按照从第一步到第三步循环按键:
若一开始输入的数据为5,那么第2022步之后,显示的结果是( )
A、5 B、 C、 D、2511. 图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( ) A、 B、 C、 D、12. 如图,在平行四边形中, , , , 是边的中点,是线段上的动点,将沿所在直线折叠得到 , 连接 , 则的最小值是( )
A、 B、 C、 D、12. 如图,在平行四边形中, , , , 是边的中点,是线段上的动点,将沿所在直线折叠得到 , 连接 , 则的最小值是( ) A、 B、6 C、4 D、
A、 B、6 C、4 D、二、填空题
-
13. 分解因式: .14. 一副三角板按如图所示叠放,其中 , , , 且 , 则度.
 15. 如图,四边形的顶点坐标分别为 , , , , 当过点B的直线l将四边形的面积分成面积相等的两部分时,则直线l的函数表达式为 .
15. 如图,四边形的顶点坐标分别为 , , , , 当过点B的直线l将四边形的面积分成面积相等的两部分时,则直线l的函数表达式为 . 16. 若不等式对恒成立则x的取值范围是 .17. 如图,在平面直角坐标系中有两条直线 , ,若 上的一点 到 的距离是 ,则点 的坐标为 .
16. 若不等式对恒成立则x的取值范围是 .17. 如图,在平面直角坐标系中有两条直线 , ,若 上的一点 到 的距离是 ,则点 的坐标为 .
三、解答题
-
18. 解不等式19. 如图,四边形ABCD是平行四边形,E,F是对角线AC的三等分点,连接BE,DF.证明BE=DF.
 20. “五水共治”吹响了浙江大规模环境保护的号角,小明就自己家所在的小区“家庭用水量”进行了一次调查,小明把一个月家庭用水量分成四类:A类用水量为10吨以下;B类用水量为10-20吨:C类用水量为20-30吨;D类用水量为30吨以上,图1和图2是他根据采集的数据绘制的两幅不完整的统计图,请根据图中提供的信息解答以下问题:
20. “五水共治”吹响了浙江大规模环境保护的号角,小明就自己家所在的小区“家庭用水量”进行了一次调查,小明把一个月家庭用水量分成四类:A类用水量为10吨以下;B类用水量为10-20吨:C类用水量为20-30吨;D类用水量为30吨以上,图1和图2是他根据采集的数据绘制的两幅不完整的统计图,请根据图中提供的信息解答以下问题: (1)、求小明此次调查了多少个家庭?(2)、已知B类,C类的家庭数之比为3∶4,根据两图信息,求出B类和C类分别有多少户家庭?(3)、补全条形统计图,并计算出扇形统计图中“C类”部分所对应的扇形的圆心角的度数;(4)、如果小明所住小区共有1500户,请估算全小区属于A类节水型家庭有多少户?21. 小李午休时从单位出发,到距离单位2000米的书店去买书,他先步行800米后,换骑公共自行车(自行车投放点固定)到达书店,全程用时15分钟.已知小李骑自行车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).(1)、分别求小李步行和骑自行车的平均速度;(2)、买完书后,小李原路返回,采取先骑公共自行车后步行.此时离上班时间只剩10分钟,为按时上班,他的骑行速度提升到原来的1.5倍.问:小李按原来的步行速度能按时到单位吗?若不行,他的步行速度至少提升到多少(米/分)?22. 如图,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4.
(1)、求小明此次调查了多少个家庭?(2)、已知B类,C类的家庭数之比为3∶4,根据两图信息,求出B类和C类分别有多少户家庭?(3)、补全条形统计图,并计算出扇形统计图中“C类”部分所对应的扇形的圆心角的度数;(4)、如果小明所住小区共有1500户,请估算全小区属于A类节水型家庭有多少户?21. 小李午休时从单位出发,到距离单位2000米的书店去买书,他先步行800米后,换骑公共自行车(自行车投放点固定)到达书店,全程用时15分钟.已知小李骑自行车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).(1)、分别求小李步行和骑自行车的平均速度;(2)、买完书后,小李原路返回,采取先骑公共自行车后步行.此时离上班时间只剩10分钟,为按时上班,他的骑行速度提升到原来的1.5倍.问:小李按原来的步行速度能按时到单位吗?若不行,他的步行速度至少提升到多少(米/分)?22. 如图,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4. (1)、求点C的坐标;(2)、连接MG、BC,求证:MG∥BC.23. 如图1,菱形ABCD与菱形GECF的顶点C重合,点G在对角线AC上,且∠BCD=∠ECF=60°,
(1)、求点C的坐标;(2)、连接MG、BC,求证:MG∥BC.23. 如图1,菱形ABCD与菱形GECF的顶点C重合,点G在对角线AC上,且∠BCD=∠ECF=60°,
 (1)、问题发现的值为;(2)、探究与证明:将菱形GECF绕点C按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)、拓展与运用:菱形GECF在旋转过程中,当点A,G,F三点在一条直线上时,如图3所示连接CG并延长,交AD于点H,若CE=2,GH= , 则AH的长为 .24. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过两点,与轴的另一交点为点 .
(1)、问题发现的值为;(2)、探究与证明:将菱形GECF绕点C按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)、拓展与运用:菱形GECF在旋转过程中,当点A,G,F三点在一条直线上时,如图3所示连接CG并延长,交AD于点H,若CE=2,GH= , 则AH的长为 .24. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过两点,与轴的另一交点为点 . (1)、求抛物线的函数表达式;(2)、点为直线上方抛物线上一动点;
(1)、求抛物线的函数表达式;(2)、点为直线上方抛物线上一动点;①连接 , 设直线交线段于点的积为的面积为 , 求的最大值;
②过点作 , 垂足为点 , 连接 , 是否存在点 . 使得中的某个角恰好等于的2倍?若存在,求点的横坐标;若不存在,请说明理由.