山东省枣庄滕州市2022年中考二模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $b^{3} \cdot b^{3} = 2 b^{3}$ B、 $(x + 2) (x - 2) = x^{2} - 2$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 ${(- 2 a)}^{2} = 4 a^{2}$

查看试题解析
2. 下列六个数：6， $- \frac{22}{7}$ ， 3.1415， $π$ ， 0， $\sqrt{3}$ 其中无理数的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
3. 一个几何体如图所示，它的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的是（）

A、如果两个圆周角相等，那么它们所对的弧长一定相等 B、顺次连接菱形的四边中点得到的四边形是矩形 C、对于函数 $y = k x + b$ （ $k \neq 0$ ）， $y$ 的值随着 $x$ 值的增大而增大 D、立方根等于它本身的数一定是1和0

查看试题解析
5. 如图，已知一次函数 $y = m x + n$ 的图象经过点 $P (- 2 ， 3)$ ，则关于 $x$ 的不等式 $m x + n < 3$ 的解集为（）

A、 $x > - 3$ B、 $x < - 3$ C、 $x > - 2$ D、 $x < - 2$

查看试题解析
6. 如图， $A I$ 、 $B I$ 、 $C I$ 分别平分 $∠ B A C$ 、 $∠ A B C$ 、 $∠ A C B$ ， $I D ⊥ B C$ ， $△ A B C$ 的周长为18， $I D = 3$ ，则 $△ A B C$ 的面积为（）

A、18 B、30 C、24 D、27

查看试题解析
7. 如图，一束太阳光线平行照射在放置于地面的正六边形上，若 $∠ 1 = 19 °$ ，则 $∠ 2$ 的度数为（）

A、 $41 °$ B、 $51 °$ C、 $42 °$ D、 $49 °$

查看试题解析
8. 如图，矩形 $A B C D$ 四个顶点的坐标分别为 $A (- 1 ， 2)$ ， $B (- 1 ， - 1)$ ， $C (3 ， - 1)$ ， $D (3 ， 2)$ ．当双曲线 $y = \frac{k}{x}$ （ $k > 0$ ）与矩形只有两个交点时， $k$ 的取值范围是（）

A、 $0 < k < 6$ B、 $1 < k < 6$ C、 $k > 1$ D、 $0 < k < 1$

查看试题解析
9. 如图，一块直角三角板的30°角的顶点 $P$ 落在 $⊙ O$ 上，两边分别交 $⊙ O$ 于 $A$ 、 $B$ 两点，若 $⊙ O$ 的直径为10，则弦 $A B$ 长为（）

A、10 B、5 C、 $5 \sqrt{3}$ D、 $\frac{5 \sqrt{3}}{2}$

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + c$ （ $a > 0$ ），且 $a + b + c = - \frac{1}{2}$ ， $a - b + c = - \frac{3}{2}$ ．给出下列结论：
① $a b c < 0$ ；② $2 a + 2 b + c > 0$ ；③抛物线与 $x$ 轴正半轴必有一个交点；④当 $2 \leq x \leq 3$ 时， $y_{最小值} = 3 a$ ；⑤该抛物线与直线 $y = x - c$ 有两个交点．其中正确结论的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

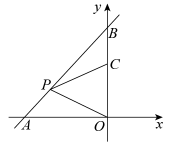
11. 解决全人类温饱问题是“世界杂交水稻之父”袁隆平先生的毕生追求.2021年中国粮食总产量达到1370000000000吨，已成为世界粮食第一大国．将1370000000000用科学记数法表示为．

查看试题解析
12. 已知关于x的一元二次方程 $x^{2} + 2 x - 1 + m = 0$ 有两个实数根，则实数m的取值范围是．

查看试题解析
13. 人们把 $\frac{\sqrt{5} - 1}{2}$ 这个数叫做黄金分割数，著名数学家华罗庚优选法中的0.618法就应用了黄金分割数．设 $a = \frac{\sqrt{5} - 1}{2}$ ， $b = \frac{\sqrt{5} + 1}{2}$ ，得 $a b = 1$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $S_{2} = \frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ ， $S_{3} = \frac{1}{1 + a^{3}} + \frac{1}{1 + b^{3}}$ ， …，则 $S_{1} + S_{2} + \cdot \cdot \cdot + S_{2022} =$ ．

查看试题解析
14. 如图，一次函数y＝x＋2的图像与坐标轴分别交于A，B两点，点P，C分别是线段AB，OB上的点，且∠OPC＝45°，PC＝PO，则点P的坐标为．

查看试题解析
15. 如图，在平面直角坐标系中，正方形 $O A B C$ 的边 $O C$ 、 $O A$ 分别在 $x$ 轴和 $y$ 轴上， $O A = 5$ ，点 $D$ 是边 $A B$ 上靠近点 $A$ 的三等分点，将 $△ O A D$ 沿直线 $O D$ 折叠后得到 $△ O A^{'} D$ ，若反比例函数 $y = \frac{k}{x}$ （ $k \neq 0$ ）的图象经过 $A^{'}$ 点，则 $k$ 的值为．

查看试题解析
16. 如图，点 $P$ 是 $∠ A O B$ 内任意一点， $O P = 3 c m$ ，点 $M$ 和点 $N$ 分别是射线 $O A$ 和射线 $O B$ 上的动点， $∠ A O B = 30 °$ ，则 $△ P M N$ 周长的最小值是．

查看试题解析

三、解答题

17. 化简求值： $(1 - \frac{3 a - 10}{a - 2}) \div (\frac{a - 4}{a^{2} - 4 a + 4})$ ，其中 $a$ 与2，3构成三角形的三边，且 $a$ 为整数.

查看试题解析
18. “2021湖南红色文化旅游节——重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行．该镇南面山坡上有一座宝塔，一群爱好数学的学生在研学之余对该宝塔的高度进行了测量．如图所示，在山坡上的A点测得塔底B的仰角 $∠ B A C = 13 °$ ，塔顶D的仰角 $∠ D A C = 38 °$ ，斜坡 $A B = 50$ 米，求宝塔 $B D$ 的高（精确到1米）（参考数据： $s i n 13 ° \approx 0.22 ， c o s 13 ° \approx 0.97 ， t a n 13 ° \approx 0.23 ， s i n 38 ° \approx 0.62 ， c o s 38 ° \approx 0.79 ， t a n 38 ° \approx 0.78$ ）

查看试题解析
19. 某学校为了解学生关于新冠病毒防疫常识的掌握情况，特开展了网络防疫测试．某小组随机抽取部分学生的测试成绩 $x$ （满分100分），并进行整理分析，绘制了如下不完整的统计图表．
学生测试成绩频数分布表
组别
成绩 $x$ /分
人数
$A$
$60 \leq x < 70$
$n$
$B$
$70 \leq x < 80$
9
$C$
$80 \leq x < 90$
12
$D$
$90 \leq x \leq 100$
6
根据以上信息，回答下列问题：

(1)、本次共抽取了名学生的测试成绩．

(2)、m= ， n= ．

(3)、 $D$ 组中成绩优异的前四名学生有2名男生和2名女生，学校从中选出两名担任学校防疫宣传员，请你用列表或树状图的方式，求选出一名男生和一名女生的概率．

查看试题解析
20. 为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具．已知购进2件甲种农机具和1件乙种农机具共需3.5万元，购进1件甲种农机具和3件乙种农机具共需3万元．

(1)、求购进1件甲种农机具和1件乙种农机具各需多少万元？

(2)、若该粮食生产基地计划购进甲、乙两农机具共10件，且投入资金不少于9.8万元又不超过12万元，则有几种购买方案？哪种购买方案需要的资金最少，最少资金是多少？

查看试题解析
21. 如图，在平面直角坐标系中， $R t △ A B C$ 的顶点 $A$ ， $B$ 在函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）的图象上， $A C ∥ x$ 轴，线段 $A B$ 的垂直平分线交 $C B$ 于点 $M$ ，交 $A C$ 的延长线于点 $E$ ，点 $A$ 纵坐标为2，点 $B$ 横坐标为1， $C E = 1$ ．连接 $B E$ ．

(1)、求点 $E$ 的坐标及 $k$ 的值；

(2)、求 $△ M B E$ 的面积．

查看试题解析
22. 定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“直角等邻对补”四边形，简称“直等补”四边形．根据以上定义，解决下列问题：

(1)、如图1，正方形 $A B C D$ 中 $E$ 是 $C D$ 上的点，将 $△ B C E$ 绕 $B$ 点旋转，使 $B C$ 与 $B A$ 重合，此时点 $E$ 的对应点 $F$ 在 $D A$ 的延长线上，则四边形 $B E D F$ （填“是”或“不是”）“直等补”四边形；

(2)、如图2，已知四边形 $A B C D$ 是“直等补”四边形， $A B = B C$ ， $A D > A B$ ，过点 $B$ 作 $B E ⊥ A D$ 于点 $E$ ．
①试探究 $B E$ 与 $D E$ 的数量关系，并说明理由；
②若 $B C = 10$ ， $C D = 2$ ，求 $A D$ 的长．

查看试题解析
23. 如图，在△ABC中，AB=AC，以AC边为直径作 $⊙$ O交BC边于点D，过点D作DE⊥AB于点E，ED、AC的延长线交于点F.

(1)、求证：EF是 $⊙$ O的切线；

(2)、若EB=6，且sin∠CFD= $\frac{3}{5}$ ，求 $⊙$ O的半径.

查看试题解析
24. 抛物线 $y = - x^{2} + 2 x + 3$ 与 $x$ 轴交于另一点 $A$ ， $B$ 两点．与 $y$ 轴交于 $C$ ， $D$ 为抛物线的顶点．

(1)、求 $A$ ， $B$ ， $C$ ， $D$ 的坐标；

(2)、点 $P$ 为抛物线上的点，且 $△ P A C$ 是直角三角形，求点 $P$ 的坐标．

(3)、点 $M$ 是 $y$ 轴上一动点，点 $Q$ 为平面内任意一点，当以 $A$ ， $D$ ， $M$ ， $Q$ 为顶点的四边形是矩形，直接写出点 $Q$ 的坐标．

查看试题解析

组别	成绩 $x$ /分	人数
$A$	$60 \leq x < 70$	$n$
$B$	$70 \leq x < 80$	9
$C$	$80 \leq x < 90$	12
$D$	$90 \leq x \leq 100$	6