山东省枣庄市市中区2022年中考数学一模试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、-2 B、2 C、 D、2. 下列运算正确的是( )A、x3+x3=2x6 B、x2·x3=x6 C、x3÷x=x3 D、(-2x2)3=-8x63. 据报道,截至2022年3月24日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗约324300万剂次.将数据324300万用科学记数法表示为( )A、32.43×104 B、3.243×105 C、3.243×109 D、32.43×1084. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
 A、95° B、100° C、105° D、110°5. 帅帅收集了南街米粉店今年6月1日至6月5日每天的用水量(单位:吨),整理并绘制成如下折线统计图.下列结论正确的是( )
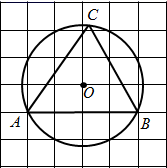
A、95° B、100° C、105° D、110°5. 帅帅收集了南街米粉店今年6月1日至6月5日每天的用水量(单位:吨),整理并绘制成如下折线统计图.下列结论正确的是( ) A、极差是6 B、众数是7 C、中位数是5 D、方差是86. 如图,点A,B,C为⊙O上的三点,∠AOB=∠BOC,∠ACB=10°,则∠AOC的度数为( )
A、极差是6 B、众数是7 C、中位数是5 D、方差是86. 如图,点A,B,C为⊙O上的三点,∠AOB=∠BOC,∠ACB=10°,则∠AOC的度数为( ) A、90° B、80° C、70° D、60°7. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、
A、90° B、80° C、70° D、60°7. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、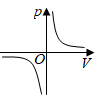 B、
B、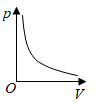 C、
C、 D、
D、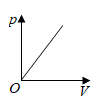 8. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为 株,则正确的方程是( )A、 B、 C、 D、9. 如图,在四边形纸片中, , , . 将纸片折叠,使点落在边上的点处,折痕为 . 若 , 则的长为( )
8. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为 株,则正确的方程是( )A、 B、 C、 D、9. 如图,在四边形纸片中, , , . 将纸片折叠,使点落在边上的点处,折痕为 . 若 , 则的长为( )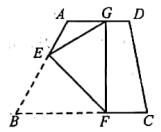 A、5 B、 C、 D、10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法中,错误的是( )
A、5 B、 C、 D、10. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法中,错误的是( ) A、当﹣1<x<2时,y<0 B、a+c=b C、当x>时,y随x的增大而增大 D、若顶点坐标为 , 则方程ax2+bx+c=m﹣1有实数根
A、当﹣1<x<2时,y<0 B、a+c=b C、当x>时,y随x的增大而增大 D、若顶点坐标为 , 则方程ax2+bx+c=m﹣1有实数根二、填空题
-
11. 已知二元一次方程x+3y=14,请写出该方程的一组整数解 .12. 已知a+b=2,a﹣b=3.则a2﹣b2的值为 .13. 如图,在正方形网格中,每个小正方形的边长都是1, 是 的外接圆,点A , B , O在网格线的交点上,则 的值是 .
 14. 如图,在平面直角坐标系xOy中,点A在第一象限内,点B在x轴正半轴上,△OCD是以点O为位似中心,且与△OAB的相似比为的位似图形.若点A的坐标为(3,2),则点C的坐标为 .
14. 如图,在平面直角坐标系xOy中,点A在第一象限内,点B在x轴正半轴上,△OCD是以点O为位似中心,且与△OAB的相似比为的位似图形.若点A的坐标为(3,2),则点C的坐标为 . 15. 数形结合是解决数学问题常用的思想方法.如图,直线与直线相交于点 . 根据图象可知,关于x的不等式的解集是
15. 数形结合是解决数学问题常用的思想方法.如图,直线与直线相交于点 . 根据图象可知,关于x的不等式的解集是 16. 如图,在Rt△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=26,BG=10,则CF的长为 .
16. 如图,在Rt△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=26,BG=10,则CF的长为 .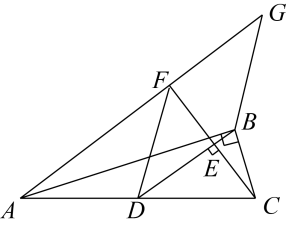
三、解答题
-
17. 计算: .18. 以下是小明同学解方程的过程.
方程两边同时乘(x-3),得1-x=-1-2 第一步
解得x=4 第二步
检验:当x=4时,x-3 =4-3 =1≠0. 第三步
所以,原分式方程的解为x=4. 第四步
(1)、小明的解法从第步开始出现错误(2)、写出解方程的正确过程.19. 如图,在菱形ABCD中,AD=4 (1)、用尺规作图,作出边AB的垂直平分线(不写作法,保留作图痕迹);(2)、若(1)中作的AB的垂直平分线交对角线BD于点G,连接GA,GA恰好垂直于边AD,求菱形ABCD的面积.20. 某校为了加强同学们的安全意识,随机抽取部分同学进行了一次安全知识测试,按照测试成绩分为优秀、良好、合格和不合格四个等级,绘制了如下不完整的统计图.
(1)、用尺规作图,作出边AB的垂直平分线(不写作法,保留作图痕迹);(2)、若(1)中作的AB的垂直平分线交对角线BD于点G,连接GA,GA恰好垂直于边AD,求菱形ABCD的面积.20. 某校为了加强同学们的安全意识,随机抽取部分同学进行了一次安全知识测试,按照测试成绩分为优秀、良好、合格和不合格四个等级,绘制了如下不完整的统计图. (1)、参加测试的学生人数为 , 等级为优秀的学生的比例为;(2)、该校有600名学生,请估计全校安全意识较强(测试成绩能达到良好以上等级)的学生人数;(3)、成绩为优秀的甲、乙两位同学被选中与其他学生一起参加安全宣讲活动,该活动随机分为A,B,C三组.求甲、乙两人恰好分在同一组的概率.21. 某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于38元,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间符合一次函数关系,如图所示.
(1)、参加测试的学生人数为 , 等级为优秀的学生的比例为;(2)、该校有600名学生,请估计全校安全意识较强(测试成绩能达到良好以上等级)的学生人数;(3)、成绩为优秀的甲、乙两位同学被选中与其他学生一起参加安全宣讲活动,该活动随机分为A,B,C三组.求甲、乙两人恰好分在同一组的概率.21. 某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于38元,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间符合一次函数关系,如图所示. (1)、求y与x之间的函数关系式;(2)、设商场销售这种商品每天获利w(元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润是多少?22. 已知正方形OABC的面积为9,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=(x>0,k>0)的图象上,点P(m,n)是函数y=(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若矩形OEPF和正方形OABC不重合部分(阴影)面积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(1)、求y与x之间的函数关系式;(2)、设商场销售这种商品每天获利w(元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润是多少?22. 已知正方形OABC的面积为9,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=(x>0,k>0)的图象上,点P(m,n)是函数y=(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若矩形OEPF和正方形OABC不重合部分(阴影)面积为S.(提示:考虑点P在点B的左侧或右侧两种情况) (1)、求B点的坐标和k的值;(2)、写出S关于m的函数关系式;(3)、当S=3时,求点P的坐标.23. 如图,AB是的直径,与交于点A,点E是半径上一点(点E不与点O,A重合).连接DE交于点C,连接 , . 若 , .
(1)、求B点的坐标和k的值;(2)、写出S关于m的函数关系式;(3)、当S=3时,求点P的坐标.23. 如图,AB是的直径,与交于点A,点E是半径上一点(点E不与点O,A重合).连接DE交于点C,连接 , . 若 , .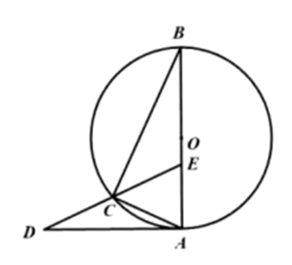 (1)、求证:AD是的切线.(2)、若 , , 则的长是 .24. 如图1,二次函数y=a(x+3)(x﹣4)的图象交坐标轴于点A,B(0,﹣2),点P为x轴上一动点.
(1)、求证:AD是的切线.(2)、若 , , 则的长是 .24. 如图1,二次函数y=a(x+3)(x﹣4)的图象交坐标轴于点A,B(0,﹣2),点P为x轴上一动点. (1)、求该二次函数的解析式;(2)、过点P作PQ⊥x轴,分别交线段AB、抛物线于点Q,C,连接AC.若OP=1,求△ACQ的面积;(3)、如图2,连接PB,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.25. 已知 和 都是等腰直角三角形 , .
(1)、求该二次函数的解析式;(2)、过点P作PQ⊥x轴,分别交线段AB、抛物线于点Q,C,连接AC.若OP=1,求△ACQ的面积;(3)、如图2,连接PB,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.25. 已知 和 都是等腰直角三角形 , . (1)、如图1,连接 , ,求证: ;(2)、将 绕点O顺时针旋转.
(1)、如图1,连接 , ,求证: ;(2)、将 绕点O顺时针旋转.①如图2,当点M恰好在 边上时,求证: ;
②当点A , M , N在同一条直线上时,若 , ,请直接写出线段 的长.