山东省泰安市泰山区2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 如图所示物体的左视图是( )
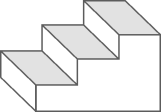 A、
A、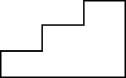 B、
B、 C、
C、 D、
D、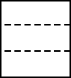 2. 中国的陆地面积和领水面积共约9970000km2 , 9970000这个数用科学记数法可表示为( )A、9.97×105 B、99.7×105 C、9.97×106 D、0.997×1073. 下列运算正确的是( )A、 B、 C、 D、4. 图,有一块含有角的直角三角板的两个顶点放在直尺的对边上.如果 , 那么的度数是( )
2. 中国的陆地面积和领水面积共约9970000km2 , 9970000这个数用科学记数法可表示为( )A、9.97×105 B、99.7×105 C、9.97×106 D、0.997×1073. 下列运算正确的是( )A、 B、 C、 D、4. 图,有一块含有角的直角三角板的两个顶点放在直尺的对边上.如果 , 那么的度数是( ) A、 B、 C、 D、5. 如图,点B,C,D在上,若 , 则的度数是( )
A、 B、 C、 D、5. 如图,点B,C,D在上,若 , 则的度数是( )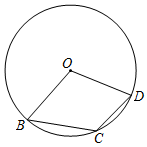 A、 B、 C、 D、6. 抛掷一枚质地均匀的普通骰子2次,朝上一面的点数之和可能为2,3,4,5,6,7,8,9,10,11,12,其中概率最大的是( )A、5 B、6 C、7 D、87. 甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字个数的统计结果如下表:
A、 B、 C、 D、6. 抛掷一枚质地均匀的普通骰子2次,朝上一面的点数之和可能为2,3,4,5,6,7,8,9,10,11,12,其中概率最大的是( )A、5 B、6 C、7 D、87. 甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字个数的统计结果如下表:班级
参赛人数
平均数
中位数
方差
甲班
55
135
149
191
乙班
55
135
151
110
小明同学分析该表后得出如下结论:①甲、乙两班学生的平均成绩相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的个数为优秀);③甲班成绩的波动比乙班大;④甲、乙两班成绩的众数相同.上述结论中,正确的是( )
A、①② B、②③ C、①③ D、①②③8. 下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有( )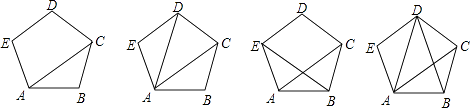 A、1个 B、2个 C、3个 D、4个9. 如图,在中,P为边上一点.若M为的中点, , 则的长为( )
A、1个 B、2个 C、3个 D、4个9. 如图,在中,P为边上一点.若M为的中点, , 则的长为( )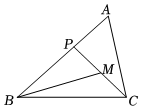 A、1 B、2 C、 D、310. 如图,在边长为1的正方形中,对角线的中点为O,分别以点A,C为圆心,以的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为( )
A、1 B、2 C、 D、310. 如图,在边长为1的正方形中,对角线的中点为O,分别以点A,C为圆心,以的长为半径画弧,分别与正方形的边相交,则图中的阴影部分的面积为( )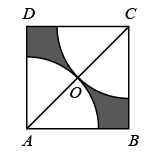 A、 B、 C、 D、11. 如图,抛物线与x轴交于点 , 其对称轴为直线 , 结合图象给出下列结论:①;②;③;④ . 其中正确的结论有( )
A、 B、 C、 D、11. 如图,抛物线与x轴交于点 , 其对称轴为直线 , 结合图象给出下列结论:①;②;③;④ . 其中正确的结论有( )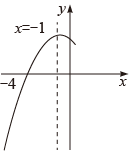 A、1个 B、2个 C、3个 D、4个12. 图,已知 , 点C在线段上,且 , 以为一边向上作等边 , 再以为直角边向右作 , 使 , F为斜边的中点,连接 , 随着边长的变化,长也在改变,则长的最小值为( )
A、1个 B、2个 C、3个 D、4个12. 图,已知 , 点C在线段上,且 , 以为一边向上作等边 , 再以为直角边向右作 , 使 , F为斜边的中点,连接 , 随着边长的变化,长也在改变,则长的最小值为( )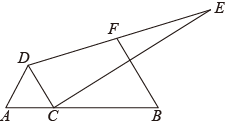 A、10 B、9 C、8 D、6
A、10 B、9 C、8 D、6二、填空题
-
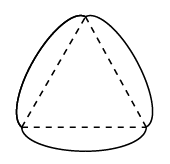
13. 已知等腰三角形的一个外角为 ,则它的顶角的度数为 .14. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则正确的方程组是15. 关于x的一元二次方程有两个不相等的实数根,则m的最小整数值是 .16. 如图,分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为4,则勒洛三角形的周长为: .
 17. 如图,在Rt△ABC中,∠BAC=90°,且BA=6,AC=8,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为.
17. 如图,在Rt△ABC中,∠BAC=90°,且BA=6,AC=8,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为. 18. 如图,在平面直角坐标系中,函数和的图象分别为直线 , 过点作x轴的垂线交于点 , 过点作y轴的垂线交于点 , 过点作x轴的垂线交于点 , 过点作y轴的垂线交于点 , …,依次进行下去,则点的坐标为 .
18. 如图,在平面直角坐标系中,函数和的图象分别为直线 , 过点作x轴的垂线交于点 , 过点作y轴的垂线交于点 , 过点作x轴的垂线交于点 , 过点作y轴的垂线交于点 , …,依次进行下去,则点的坐标为 .
三、解答题
-
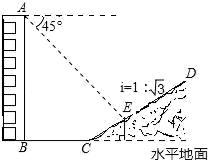
19. 解答:(1)、先化简,再求值: , 其中 .(2)、解不等式组20. 如图,一幢楼房后有一假山,其坡度为 , 山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离米,与亭子距离米,小丽从楼房顶测得E点的俯角为 , 求楼房的高.
 21. 如图,中, , , P为内部一点,且 .
21. 如图,中, , , P为内部一点,且 .
求证:
(1)、;(2)、 .22. 图,点 , 是直线与反比例函数图象的两个交点,轴,垂足为点C,已知 , 连接 , , .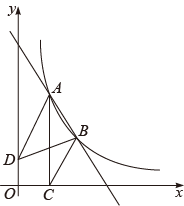 (1)、求反比例函数和直线的表达式;(2)、和的面积分别为 , , 求 .23. 随着人们“环保低碳,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车商行经营的A型自行车去年销售总额为10万元.今年该型自行车每辆售价预计比去年降低180元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元?(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2300元,应如何组织进货才能使这批自行车销售获利最多?24. 如图,在平面直角坐标系中,是直角三角形, , , , , 抛物线经过A,B两点,抛物线的顶点为D.
(1)、求反比例函数和直线的表达式;(2)、和的面积分别为 , , 求 .23. 随着人们“环保低碳,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车商行经营的A型自行车去年销售总额为10万元.今年该型自行车每辆售价预计比去年降低180元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)、A型自行车去年每辆售价多少元?(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2300元,应如何组织进货才能使这批自行车销售获利最多?24. 如图,在平面直角坐标系中,是直角三角形, , , , , 抛物线经过A,B两点,抛物线的顶点为D. (1)、求顶点D的坐标;(2)、点E是斜边上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段的长度最大时,求点E、F的坐标;(3)、在(2)的条件下,在抛物线上是否存在一点P,使是以为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.25. 解答:(1)、如图1,菱形的顶点E、H在菱形的边上,且 , 请直接写出的结果(不必写计算过程);
(1)、求顶点D的坐标;(2)、点E是斜边上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段的长度最大时,求点E、F的坐标;(3)、在(2)的条件下,在抛物线上是否存在一点P,使是以为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.25. 解答:(1)、如图1,菱形的顶点E、H在菱形的边上,且 , 请直接写出的结果(不必写计算过程);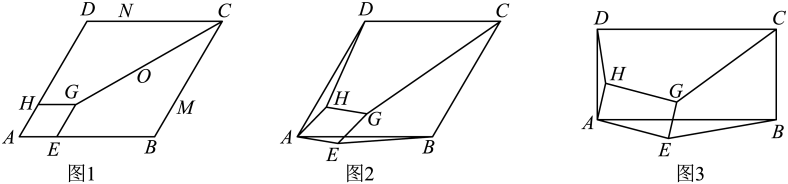 (2)、将图1中的菱形绕点A旋转一定角度,如图2,求;(3)、把图2中的菱形都换成矩形,如图3,且 , 此时的结果与(2)小题的结果相比有变化吗?如果有变化,求出变化后的结果;若无变化,请说明理由.
(2)、将图1中的菱形绕点A旋转一定角度,如图2,求;(3)、把图2中的菱形都换成矩形,如图3,且 , 此时的结果与(2)小题的结果相比有变化吗?如果有变化,求出变化后的结果;若无变化,请说明理由.