山东省泰安市高新区2022年中考数学一模试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列四个数:3,-0.5, , 中,绝对值最小的数是( )A、3 B、 C、 D、2. 下列运算结果正确的是( )A、 B、 C、 D、3. 甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )
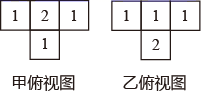 A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同4. 如图,直线 , 点是上一点,的角平分线交于点 , 若 , , 则的大小为( )
A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同4. 如图,直线 , 点是上一点,的角平分线交于点 , 若 , , 则的大小为( ) A、136° B、148° C、146° D、138°5. 某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是 ( )
A、136° B、148° C、146° D、138°5. 某校为了解学生的课外阅读情况,随机抽取了一个班的学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则该班学生一周课外阅读时间的中位数和众数分别是 ( )读书时间
6 小时及以下
7 小时
8 小时
9 小时
10 小时及以上
学生人数
6
11
8
8
7
A、8,7 B、8,8 C、8.5,8 D、8.5,76. 《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为:把一份文件慢马送到900里外的城市,需要的时间比规定时间多1天;如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )A、 B、 C、 D、7. 函数y=x2−6x+9向左平移m个单位后其图象恰好经过坐标原点,则m的值为( )A、2 B、1 C、3 D、1或38. 量角器圆心为 ,直径 ,一把宽为3的直尺的一边过 点且与量角器交于 、 两点,如图所示,则弧 的长为( ) A、 B、 C、 D、9. 如图,在中,的平分线交CD于点F,交AD的延长线于点E,过点C作 , 垂足为G,若 , , , 则线段CG的长为( )
A、 B、 C、 D、9. 如图,在中,的平分线交CD于点F,交AD的延长线于点E,过点C作 , 垂足为G,若 , , , 则线段CG的长为( ) A、 B、 C、 D、10. 如图,BE是的直径,点A和点D是上的两点,过点A作的切线交BE延长线于点C.若 , 则的度数是( )
A、 B、 C、 D、10. 如图,BE是的直径,点A和点D是上的两点,过点A作的切线交BE延长线于点C.若 , 则的度数是( ) A、28° B、26° C、25° D、18°11. 如图,在菱形 中, , , 分别是 , 上的点(不与端点重合),且 ,连接 , 相交于点 ,连接 与 相交于点 .下列结论:① ;② ;③ ;④若 ,则 .其中正确结论的序号是( )
A、28° B、26° C、25° D、18°11. 如图,在菱形 中, , , 分别是 , 上的点(不与端点重合),且 ,连接 , 相交于点 ,连接 与 相交于点 .下列结论:① ;② ;③ ;④若 ,则 .其中正确结论的序号是( ) A、①② B、①②④ C、②③④ D、①③④12. 如图,和都是等腰直角三角形, , , O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是( )
A、①② B、①②④ C、②③④ D、①③④12. 如图,和都是等腰直角三角形, , , O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是( )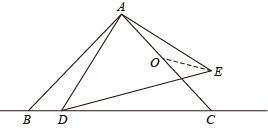 A、2 B、 C、 D、1
A、2 B、 C、 D、1二、填空题
-
13. 已知关于x的一元二次方程(1−a)x2+2x−2=0有两个不相等的实数根.则a的取值范围是 .14. 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,2小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是海里.(结果保留根号)
 15. 如图,△ABC中,AC= , 点O是AB边上的一点,⊙O与AC、BC分别相切于点A、E,点F为⊙O上一点,连AF,若四边形ACEF是菱形,则图中阴影部分面积是 .
15. 如图,△ABC中,AC= , 点O是AB边上的一点,⊙O与AC、BC分别相切于点A、E,点F为⊙O上一点,连AF,若四边形ACEF是菱形,则图中阴影部分面积是 . 16. 如图,正方形ABCD中,E为AB上一点,于点F,已知 , 过C、D、F的与边AD交于点G,则 .
16. 如图,正方形ABCD中,E为AB上一点,于点F,已知 , 过C、D、F的与边AD交于点G,则 . 17. 如图.二次函数图象的一部分与x轴的一个交点坐标为 , 对称轴为直线 , 结合图象给出下列结论:①;②;③若关于x的一元二次方程的一根是3,则另一根是;④若点 , , 均在二次函数图象上,则 . 其中正确的结论的序号为 .
17. 如图.二次函数图象的一部分与x轴的一个交点坐标为 , 对称轴为直线 , 结合图象给出下列结论:①;②;③若关于x的一元二次方程的一根是3,则另一根是;④若点 , , 均在二次函数图象上,则 . 其中正确的结论的序号为 . 18. 如图,圆心都在x轴正半轴上的半圆O1 , 半圆O2 , …,半圆On与直线l相切.设半圆O1 , 半圆O2 , …,半圆On的半径分别是r1 , r2 , …,rn,则当直线l与x轴所成锐角为α,tanα= , 且r1=1时,r2022的值是 .
18. 如图,圆心都在x轴正半轴上的半圆O1 , 半圆O2 , …,半圆On与直线l相切.设半圆O1 , 半圆O2 , …,半圆On的半径分别是r1 , r2 , …,rn,则当直线l与x轴所成锐角为α,tanα= , 且r1=1时,r2022的值是 .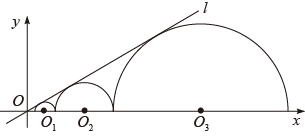
三、解答题
-
19. 计算:(1)、先化简再求值: , 其中 .(2)、解不等式: .20. 疫情期间,为了增强学生的自我保护意识,某校组织了一次全校2000名学生都参加的“新冠疫情知多少”的考试,并随机抽查了部分参赛学生的成绩,根据成绩分成如下四个组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,制作出如下的扇形统计图和条形统计图,请根据图表提供的信息解答下列问题:
 (1)、本次抽查的学生有人,扇形统计图中的m=;(2)、将条形统计图补充完整;(3)、估计全校学生中得分80分及以上的同学有多少?(4)、九(1)班在此次考试中得100分的有1位女生和3位男生,现要从九(1)班得100分的4人中选取两人代表本班去参加学校的防疫宣讲活动,请你用列表或画树状图的方法,求选出的两人恰好是一男一女的概率.21. 如图,一次函数的图象交x、y轴于A、B两点,以AB为斜边在第一象限内作等腰直角 , , 反比例函数的图象经过点C,连接OC交AB于点D.
(1)、本次抽查的学生有人,扇形统计图中的m=;(2)、将条形统计图补充完整;(3)、估计全校学生中得分80分及以上的同学有多少?(4)、九(1)班在此次考试中得100分的有1位女生和3位男生,现要从九(1)班得100分的4人中选取两人代表本班去参加学校的防疫宣讲活动,请你用列表或画树状图的方法,求选出的两人恰好是一男一女的概率.21. 如图,一次函数的图象交x、y轴于A、B两点,以AB为斜边在第一象限内作等腰直角 , , 反比例函数的图象经过点C,连接OC交AB于点D. (1)、求反比例函数的表达式;(2)、求的正切值;22. 如图,在中, , 点D在内, , , 点E在外, , .
(1)、求反比例函数的表达式;(2)、求的正切值;22. 如图,在中, , 点D在内, , , 点E在外, , . (1)、判断的形状并加以证明.(2)、连接DE,若 , , 求DE的长.23. 疫情期间,蔬菜成为人们抢购的生活物资.某蔬菜超市第一次用1200元购进某种蔬菜若干千克,以每千克8元价格很快被抢购一空.该超市第二次购买时,受疫情影响,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次购进的数量多20千克.第二次购进的该种蔬菜以每千克9元售出100千克后,因政府调控,蔬菜供应充足,为防滞销,该超市便降价50%售完剩余的蔬菜.该蔬菜超市在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?24. 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点D作于点E,作点E关于AD的对称点F,连接AF,FD,延长FD交BC的延长线于点N,交AC的延长线于点M.
(1)、判断的形状并加以证明.(2)、连接DE,若 , , 求DE的长.23. 疫情期间,蔬菜成为人们抢购的生活物资.某蔬菜超市第一次用1200元购进某种蔬菜若干千克,以每千克8元价格很快被抢购一空.该超市第二次购买时,受疫情影响,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次购进的数量多20千克.第二次购进的该种蔬菜以每千克9元售出100千克后,因政府调控,蔬菜供应充足,为防滞销,该超市便降价50%售完剩余的蔬菜.该蔬菜超市在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?24. 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点D作于点E,作点E关于AD的对称点F,连接AF,FD,延长FD交BC的延长线于点N,交AC的延长线于点M. (1)、判断AF与BD的位置关系并证明;(2)、求证:;(3)、若 , 求的值.25. 如图,抛物线经过 , 两点,与y轴交于点B,P为抛物线上的动点,连接AB,BC,PA,PC,PC与AB相交于点Q.
(1)、判断AF与BD的位置关系并证明;(2)、求证:;(3)、若 , 求的值.25. 如图,抛物线经过 , 两点,与y轴交于点B,P为抛物线上的动点,连接AB,BC,PA,PC,PC与AB相交于点Q. (1)、求抛物线的解析式;(2)、若P为第一象限抛物线上的动点,设的面积为 , 的面积为 , 当时,求点P的坐标;(3)、是否存在点P,使 , 若存在,直接写出点P的坐标:若不存在,说明理由.
(1)、求抛物线的解析式;(2)、若P为第一象限抛物线上的动点,设的面积为 , 的面积为 , 当时,求点P的坐标;(3)、是否存在点P,使 , 若存在,直接写出点P的坐标:若不存在,说明理由.