山东省寿光市2022年九年级学业水平考试数学模拟检测一（一模）

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

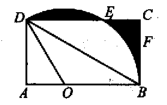
1. 下列球类图标中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，数轴上两个点分别对应实数a，b，且这两个点关于原点对称，则正确的是（）

A、 $| a | < | b |$ B、 $a + b = 0$ C、 $a b > 0$ D、 $a - b = 0$

查看试题解析
3. 2021年中国国内生产总值（GDP）超过114万亿元，大致为改革开放初期1979年国内生产总值的285倍．则数据“114万亿”用科学记数法表示为（）

A、 $114 \times 1 0^{12}$ B、 $1.14 \times 1 0^{13}$ C、 $1.14 \times 1 0^{14}$ D、 $0.114 \times 1 0^{15}$

查看试题解析
4. 如图，由4个大小相同的小正方体搭成一个几何体，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 如果 $a - 3 b = 0$ ，那么代数式 $(a - \frac{2 a b - b^{2}}{a}) \div \frac{a^{2} - b^{2}}{a}$ 的值是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $- \frac{1}{4}$ D、 $- \frac{1}{2}$

查看试题解析
6. 已知关于x的一元二次方程x²－kx＋k－3＝0的两个实数根分别为 $x_{1} ， x_{2}$ ，且 $x_{1}^{2} + x_{2}^{2} = 5$ ，则k的值是（）

A、－2 B、2 C、－1 D、1

查看试题解析
7. 下列关于过直线l外一点P作直线l的平行线的尺规作图错误的是（）

A、 B、 C、 D、

查看试题解析
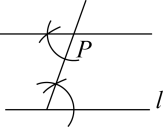8. 某短道速滑队四位队员10次训练测验的成绩如图所示，如果只选择一位成绩稳定的队员参加正式比赛，你会选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 下列各式计算正确的是（）

A、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ B、 $- 3^{- 2} = 3^{2} = 9$ C、 $2 \sqrt{2} + 3 \sqrt{3} = 5 \sqrt{5}$ D、 ${(2 a^{2} b)}^{3} = 8 a^{4} b^{3}$

查看试题解析

二、多选题

10. 如图，反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = \frac{1}{2} x + 5$ 的图象交于A，B两点，一次函数 $y = - 2 x$ 的图象经过点A．下列结论正确的是（）

A、 $k = - 8$ B、点B的坐标为 $(- 8 ， 2)$ C、连接OB，则 $S_{△ A O B} = 15$ D、点C为y轴上一动点，当△ABC的周长最小时，点C的坐标是 $(0 ， \frac{10}{3})$

查看试题解析
11. 如图所示，二次函数 $y = a (x - 1)^{2} + k (a \neq 0)$ 的图象的一部分，图像与x轴交于点 $(- 1 ， 0)$ ．下列结论中正确的是（）

A、抛物线与x轴的另一个交点坐标是 $(3 ， 0)$ B、 $a + k > 0$ C、若抛物线经过点 $(- 3 ， m)$ ，则关于x的一元二次方程 $a (x - 1)^{2} + k + m = 0$ 的两根分别为 $- 3$ ， 5 D、将抛物线向左平移3个单位，则新抛物线的表达式为 $y = a (x + 2)^{2} + k$

查看试题解析
12. 图，在边长为4的正方形ABCD中，点E，F分别是边BC，AB的中点，连接AE，DF交于点N，将 $△ A B E$ 沿AE翻折，得到 $△ A G E$ ， AG交DF于点M，延长EG交AD的延长线于点H，连接CG，ME，取ME的中点为点O，连接NO，GO．则以下结论正确的有（）

A、 $∠ A N D = 90 °$ B、 $A H = E H$ C、 $C G ∥ A E$ D、 $S_{四边形 M N O G} = S_{△ A M D}$

查看试题解析

三、填空题

13. 因式分解：x³-9x=.

查看试题解析
14. 为提升晚高峰车辆的通行速度，某市设置潮汐车道，首条潮汐车道从市政府广场到人民公园，全程约3千米．该路段实行潮汐车道设置后，在晚高峰期间，通过该路段的车辆的行驶速度平均提升25%，行驶时间平均减少2分钟．设实施潮汐车道之前，在晚高峰期间通过该路段的车辆平均每小时行驶x千米，则可列方程为．

查看试题解析
15. 如图，AB，CD是 $⊙ O$ 的弦，且 $C D ∥ A B$ ，连接OA，OB，OC，OD，AD，BC．若 $∠ C O D + ∠ A O B = 180 °$ ， $A B = 2 \sqrt{3}$ ， $O A = 2$ ，则AD的长是．

查看试题解析
16. 如图，在平面直角坐标系中，等腰直角三角形OAB，∠A＝90°，点O为坐标原点，点B在x轴上，点A的坐标是（1，1）．若将△OAB绕点O顺时针方向依次旋转45°后得到△OA₁B₁ ， △OA₂B₂ ， △OA₃B₃ ， …，可得A₁（ $\sqrt{2}$ ， 0），A₂（1，﹣1），A₃（0，﹣ $\sqrt{2}$ ），…则A₂₀₂₁的坐标是．

查看试题解析

四、解答题

17. “天宫课堂”已成为我国空间站的优秀科普活动．航天员演示了四个实验：A．浮力消失实验，B．水膜张力实验，C．水球光学实验，D．泡腾片实验．某校九年级数学兴趣小组成员随机抽取了本年级的部分同学，调查他们在这四个实验中最感兴趣的一个，并绘制了两幅不完整的统计图，如图所示：
请你根据以上信息．解答下列问题：

(1)、本次调查的总人数为人，扇形统计图中“A”所在扇形的圆心角的度数为°．C所占的百分比为，并补全条形统计图．

(2)、估计该校九年级800名学生中对“B．水膜张力实验”最感兴趣的学生人数？

(3)、从数学兴趣小组推荐的4名同学（其中有一名男生，三名女生）中随机抽取两名参加全市的比赛，请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率．

查看试题解析
18. 在抗击新冠肺炎疫情期间，某小区购买酒精和消毒液两种消毒物资，供居民使用．第一次购买酒精和消毒液若干，酒精每桶30元，消毒液每桶20元，共花费了600元；第二次又购买了与第一次相同数量的酒精和消毒液，由于酒精和消毒液每桶价格分别下降了20%和10%，只花费了510元．

(1)、求每次购买的酒精和消毒液分别是多少桶？

(2)、现有280元，若按照第二次购买的单价再次购买，根据需要，购买的酒精数量是消毒液数量的3倍，则最多能购买酒精多少瓶？

查看试题解析
19. 某数学兴趣小组在数学活动课上设计测量一棵树CD的高度，如图，测得斜坡BE的坡度 $i = 1 ： 5$ ，坡底AE的长为10米，在B处测得树CD顶部D的仰角为30°，在E处测得树CD顶部D的仰角为60°，求树高CD．（结果保留根号）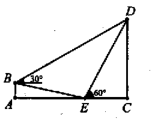

查看试题解析
20. 在北京冬奥自由式滑雪女子大跳台决赛上，中国选手谷爱凌凭借精彩发挥夺得金牌，创造历史．如图1是跳台比赛场地的示意图，在图2中取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系，图中的抛物线 $C_{1} ： y = - \frac{1}{12} x^{2} + \frac{7}{6} x + 1$ 近似表示滑雪场地上的一座小山坡，某运动员从点O正上方4米处的A点滑出，滑出后沿一段抛物线 $C_{2} ： y = - \frac{1}{8} x^{2} + b x + c$ 运动．

(1)、当运动员运动到离A处的水平距离为4米时，离水平线的高度为8米，求抛物线 $C_{2}$ 的函数解析式（不要求写出自变量x的取值范围）；

(2)、在（1）的条件下，当运动员运动的水平距离为多少米时，运动员与小山坡的竖直距离H取到最大值？最大值为多少？

查看试题解析
21. 如图，在矩形ABCD中， $A B = 1$ ， $A D = 3$ ， E为AD边的一动点（不与端点重合），连接CE并延长，交BA的延长线于点F，延长EA至点G，使 $A G = A E$ ，分别连接BE，BG，FG．

(1)、在点E的运动过程中，四边形BEFG能否成为菱形？请判断并说明理由．

(2)、若 $△ B A E$ 与 $△ E D C$ 相似，求AE的长．

查看试题解析
22. 如图，在直角坐标系中， $B (0 ， 4)$ ， $D (5 ， 0)$ ，一次函数 $y = \frac{4}{11} x + \frac{12}{11}$ 的图象过 $C (8 ， n)$ ，与x轴交于A点．

(1)、求点A和点C坐标；

(2)、求证：四边形ABCD为平行四边形；

(3)、将 $△ A O B$ 绕点O顺时针旋转，旋转得 $△ A_{1} O B_{1}$ ，问：能否使以O、 $A_{1}$ 、D、 $B_{1}$ 为顶点的四边形是平行四边形？若能，直接写出点 $A_{1}$ 的坐标；若不能，请说明理由．

查看试题解析
23. 如图，点O是矩形ABCD中AB边上的一点，以O为圆心，OB为半径作圆， $⊙ O$ 交CD边于点E，且恰好过点D，连接BD，过点E作 $E F ∥ B D$ ．

(1)、若 $∠ B O D = 120 °$ ，证明以下结论：
①EF是 $⊙ O$ 的切线；
② $S_{阴影} = S_{△ D A O}$ ．

(2)、若 $C F = 1$ ， $F B = 2$ ，求OD的长．

查看试题解析