山东省日照市高新区2022年中考数学一模试卷
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
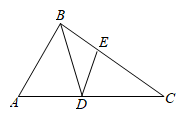
1. 的值为( )A、 B、 C、 D、22. 国家统计局2021年5月11日公布了第七次全国人口普查结果,全国总人口约14.1亿人,将14.1亿用科学记数法表示为( )A、14.1×108 B、1.41×108 C、1.41×109 D、0.141×10103. 下列等式成立的是( )A、 B、 C、 D、4. 如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )
 A、30° B、40° C、50° D、60°5. 已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )
A、30° B、40° C、50° D、60°5. 已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )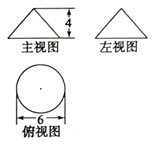 A、214° B、215° C、216° D、217°6. 已知、是一元二次方程的两个实数根,则代数式的值等于( )A、 B、 C、 D、7. 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )
A、214° B、215° C、216° D、217°6. 已知、是一元二次方程的两个实数根,则代数式的值等于( )A、 B、 C、 D、7. 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )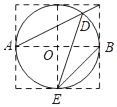 A、 B、 C、2 D、8. 如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧 ,再分别以E、F为圆心,1为半径作圆弧 、 ,则图中阴影部分的面积为( )
A、 B、 C、2 D、8. 如图,正方形ABCD的边长为2,O为对角线的交点,点E、F分别为BC、AD的中点.以C为圆心,2为半径作圆弧 ,再分别以E、F为圆心,1为半径作圆弧 、 ,则图中阴影部分的面积为( )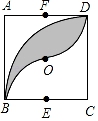 A、π﹣1 B、π﹣2 C、π﹣3 D、4﹣π9. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且10. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A、π﹣1 B、π﹣2 C、π﹣3 D、4﹣π9. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且10. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )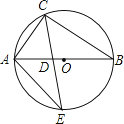 A、1: B、1: C、1:2 D、2:311. 观察下列树枝分叉的规律图,若第个图树枝数用表示,则( )
A、1: B、1: C、1:2 D、2:311. 观察下列树枝分叉的规律图,若第个图树枝数用表示,则( ) A、 B、 C、 D、12. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ( );⑤若方程 =1有四个根,则这四个根的和为2,其中正确的结论有( )
A、 B、 C、 D、12. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ( );⑤若方程 =1有四个根,则这四个根的和为2,其中正确的结论有( )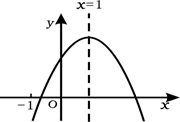 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
13. 已知、为实数,且 , 则x-y= .14. 若不等式组有解,则a的取值范围是 .15. 如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动.在运动过程中,点B到原点的最大距离是
 16. 如图,点A在双曲线的第一象限的那一支上,AB垂直于轴与点B,点C在轴正半轴上,且 , 点E在线段AC上,且 , 点D为OB的中点,若的面积为3,则k的值为 .
16. 如图,点A在双曲线的第一象限的那一支上,AB垂直于轴与点B,点C在轴正半轴上,且 , 点E在线段AC上,且 , 点D为OB的中点,若的面积为3,则k的值为 .
三、解答题
-
17.(1)、计算:;(2)、先化简,再求值: , 其中 , 满足 .18. 我市于2021年5月22-23日在遂宁观音湖举行了“龙舟赛”,吸引了全国各地选手参加.现对某校初中1000名学生就“比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制出以下两幅不完整的统计图表,请根据统计图表回答下列问题:
类别
频数
频率
不了解
10
m
了解很少
16
0.32
基本了解
b
很了解
4
n
合计
a
1
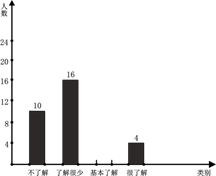 (1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.19. 荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.(1)、求购买该品牌一个台灯、一个手电筒各需要多少元?(2)、经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?20. 如图,在 中, 是直径,弦 ,垂足为 , 为 上一点, 为弦 延长线上一点,连接 并延长交直径 的延长线于点 ,连接 交 于点 ,若 .
(1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.19. 荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.(1)、求购买该品牌一个台灯、一个手电筒各需要多少元?(2)、经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?20. 如图,在 中, 是直径,弦 ,垂足为 , 为 上一点, 为弦 延长线上一点,连接 并延长交直径 的延长线于点 ,连接 交 于点 ,若 .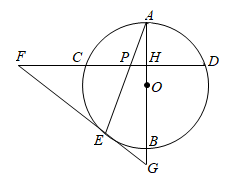 (1)、求证: 是 的切线;(2)、若 的半径为8, ,求 的长.21. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点C.抛物线的对称轴是且经过、C两点,与x轴的另一交点为点B.
(1)、求证: 是 的切线;(2)、若 的半径为8, ,求 的长.21. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点C.抛物线的对称轴是且经过、C两点,与x轴的另一交点为点B. (1)、①直接写出点B的坐标;②求抛物线解析式.(2)、若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.(3)、抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.22.(1)、发现
(1)、①直接写出点B的坐标;②求抛物线解析式.(2)、若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.(3)、抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.22.(1)、发现如图,点为线段外一动点,且 , .
填空:当点位于时,线段的长取得最大值,且最大值为.(用含 , 的式子表示)
 (2)、应用
(2)、应用点为线段外一动点,且 , .如图所示,分别以 , 为边,作等边三角形和等边三角形 , 连接 , .
①找出图中与相等的线段,并说明理由;
②直接写出线段长的最大值.
 (3)、拓展
(3)、拓展如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 点为线段外一动点,且 , , , 求线段长的最大值及此时点的坐标.
