山东省临沂市沂南县2022年九年级一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列实数中,比﹣2小的数是( )A、﹣1 B、5 C、﹣5 D、12. 计算的正确结果是( )A、 B、 C、 D、3. 如图,是放置在北京冬奥会场馆内水平地面上的领奖台,其几何体左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,直线 , 平分 , ,则 的度数是( )
4. 如图,直线 , 平分 , ,则 的度数是( )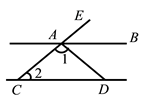 A、 B、 C、 D、5. 不等式的解集在数轴上表示为( )A、
A、 B、 C、 D、5. 不等式的解集在数轴上表示为( )A、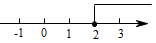 B、
B、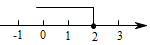 C、
C、 D、
D、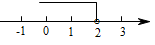 6. 如图,某市会展中心设置了一个圆形展厅,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是72°,为了观察到展厅的每个位置,最少需在圆形边缘上共安装这样的监视器( )
6. 如图,某市会展中心设置了一个圆形展厅,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是72°,为了观察到展厅的每个位置,最少需在圆形边缘上共安装这样的监视器( ) A、5台 B、4台 C、3台 D、2台7. 有两把不同的锁和三把钥匙,其中两把钥匙恰好分别能打开这两把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率是( )A、 B、 C、 D、8. 如图,在矩形中, , , 动点满足 , 则点到、两点距离之和的最小值为( )
A、5台 B、4台 C、3台 D、2台7. 有两把不同的锁和三把钥匙,其中两把钥匙恰好分别能打开这两把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率是( )A、 B、 C、 D、8. 如图,在矩形中, , , 动点满足 , 则点到、两点距离之和的最小值为( ) A、 B、 C、 D、9. 计算:(m+2+=( )A、﹣2m﹣6 B、2m+6 C、﹣m﹣3 D、m+310. 某商店促销活动,同时购买一副乒乓球拍和一副羽毛球拍可以打七折,需要花费224元.已知一副羽毛球拍标价比一副乒乓球拍标价的2倍多20元,若一副乒乓球拍的标价是x元,一副羽毛球拍的标价为y元,根据题意,可列方程组( )A、 B、 C、 D、11. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论错误的是( )
A、 B、 C、 D、9. 计算:(m+2+=( )A、﹣2m﹣6 B、2m+6 C、﹣m﹣3 D、m+310. 某商店促销活动,同时购买一副乒乓球拍和一副羽毛球拍可以打七折,需要花费224元.已知一副羽毛球拍标价比一副乒乓球拍标价的2倍多20元,若一副乒乓球拍的标价是x元,一副羽毛球拍的标价为y元,根据题意,可列方程组( )A、 B、 C、 D、11. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论错误的是( )t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
A、足球距离地面的最大高度超过20m B、足球飞行路线的对称轴是直线 C、点(10,0)在该抛物线上 D、足球被踢出时,距离地面的高度逐渐下降.12. 如图,已知是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F, . FG为的角平分线,点H在FG的延长线上, , 连接HA、HC.①;②;③;④;其中说法正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
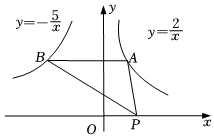
13. 分解因式 .14. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是。15. 如图,平面直角坐标系中,点A、B分别在函数与的图象上,点p在x轴上.若轴.则的面积为 .
 16. 如图1是一张圆形纸片,小明同学进行了如下连续操作:
16. 如图1是一张圆形纸片,小明同学进行了如下连续操作:
(1)将圆形纸片左右对折,上下对折,得到折痕AB与CD互相垂直,垂足为点M,如图2.
(2)将圆形纸片沿EF折叠,使BM两点重合,折痕EF与AB相交于N,连接AE、AF、BE、BF,如图3.小明得到了以下结论,其中正确的是(只填写序号).①;②;③;④四边形MEBF为菱形.
三、解答题
-
17. 计算:18. 某学校八年级共800名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:4.2,4.1,4.7,4.1,4.3,4.3,4.4,4.6,4.1,5.2,5.2,4.5,5.0,4.5,4.3,4.4,4.8,5.3,4.5,5.2,4.4,4.2,4.3,5.3,4.9,5.2,4.9,4.8,4.6,5.1,4.2,4.4,4.5,4.1,4.5,5.1,4.4,5.0,5.2,5.3根据数据绘制了如图的表格和统计图,根据下面提供的信息,回答下列问题:
等级
视力(x)
频数
频率
A
4
0.1
B
12
0.3
C
a
D
b
E
10
0.25
合计
40
1
 (1)、统计表中的 , ;(2)、请补全条形统计图;(3)、所抽取学生成绩的中位数落在等级;(4)、根据抽样调查结果,请估计该校八年级学生视力为“C级”的有多少人?19. 某校为检测师生体温,在校门安装了某型号的测温门,如图为该“测温门”截面示意图.身高1.6m米的小聪做了如下实验:当他在地面M处时“测温门”开始显示额头温度,此时在额头B处测得A的仰角为30°;当他在地面N处时,“测温门”停止显示额头温度,此时在额头C处测得A的仰角为58°.如果测温门顶部A处距地面的高度AD为2.8m,求小聪在有效测温区间MN的长度约为多少?(保留两位小数,注:额头到地面的距离以身高计, , , , . )
(1)、统计表中的 , ;(2)、请补全条形统计图;(3)、所抽取学生成绩的中位数落在等级;(4)、根据抽样调查结果,请估计该校八年级学生视力为“C级”的有多少人?19. 某校为检测师生体温,在校门安装了某型号的测温门,如图为该“测温门”截面示意图.身高1.6m米的小聪做了如下实验:当他在地面M处时“测温门”开始显示额头温度,此时在额头B处测得A的仰角为30°;当他在地面N处时,“测温门”停止显示额头温度,此时在额头C处测得A的仰角为58°.如果测温门顶部A处距地面的高度AD为2.8m,求小聪在有效测温区间MN的长度约为多少?(保留两位小数,注:额头到地面的距离以身高计, , , , . ) 20. 已知函数
20. 已知函数 (1)、当时,;(2)、已知点在函数图象上,则求m的值;(3)、已知函数的图象与函数的图象关于y轴对称,我们称为的镜像函数.请在图中画出 , 的图象.(4)、若直线与函数和的图象有且只有一个交点,请直接写出a的取值范围.21. 如图,AB为的切线,B为切点,过点B作 , 垂足为点E,交于点C,连接CO,并延长CO与AB的延长线交于点D,与交于点F,连接AC.
(1)、当时,;(2)、已知点在函数图象上,则求m的值;(3)、已知函数的图象与函数的图象关于y轴对称,我们称为的镜像函数.请在图中画出 , 的图象.(4)、若直线与函数和的图象有且只有一个交点,请直接写出a的取值范围.21. 如图,AB为的切线,B为切点,过点B作 , 垂足为点E,交于点C,连接CO,并延长CO与AB的延长线交于点D,与交于点F,连接AC. (1)、求证:AC为的切线:(2)、若半径为2, . 求阴影部分的面积.
(1)、求证:AC为的切线:(2)、若半径为2, . 求阴影部分的面积.
