山东省临沂市临沭县2022年中考一模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

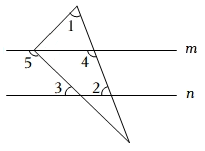
1. 清代袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为（）

A、 $8.4 × 1 0^{- 5}$ B、 $8.4 \times 1 0^{- 6}$ C、 $8.4 × 1 0^{- 7}$ D、 $8.4 \times 1 0^{6}$

查看试题解析
2. 如图，直线m∥n，三角尺的直角顶点在直线 $m$ 上，且三角尺的直角被直线 $m$ 平分，若 $∠ 1 = 6 0^{∘}$ ，则下列结论错误的是（）

A、 $∠ 2 = 7 5^{∘}$ B、 $∠ 3 = 4 5^{∘}$ C、 $∠ 4 = 10 5^{∘}$ D、 $∠ 5 = 14 5^{∘}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{9} \div a^{3} = a^{3}$ B、 $2 a^{3} + 4 a^{3} = 6 a^{6}$ C、 ${(- a^{3})}^{2} = a^{6}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
4. 如图是某工件的三视图，则此工件的表面积为（　　）

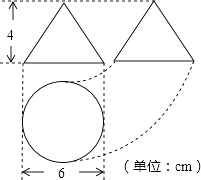A、15πcm² B、51πcm² C、66πcm² D、24πcm²

查看试题解析
5. 若不等式组 ${\begin{array}{l} \frac{x + 1}{3} < \frac{x}{2} - 1 \\ x < 4 m \end{array}$ 无解，则 $m$ 的取值范围为（）

A、 $m \leq 2$ B、 $m < 2$ C、 $m \geq 2$ D、 $m > 2$

查看试题解析
6. 某校举行“停课不停学，名师陪你在家学”活动，计划投资8000元建设几间直播教室，为了保证教学质量，实际每间建设费用增加了20%，并比原计划多建设了一间直播教室，总投资追加了4000元.根据题意，求出原计划每间直播教室的建设费用是（）

A、1600元 B、1800元 C、2000元 D、2400元

查看试题解析
7. 在对一组样本数据进行分析时，小华列出了方差的计算公式 $s^{2} = \frac{{(2 - \bar{x})}^{2} + {(3 - \bar{x})}^{2} + {(3 - \bar{x})}^{2} + {(4 - \bar{x})}^{2}}{n}$ ，由公式提供的信息，则下列说法错误的是（）

A、样本的容量是4 B、样本的中位数是3 C、样本的众数是3 D、样本的平均数是3.5

查看试题解析
8. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，点 $P$ 为边 $A D$ 上任意一点（点 $P$ 不与点 $A$ ， $D$ 重合），连接 $C P$ ．若 $∠ B = 15 0^{∘}$ ，则 $∠ A P C$ 的度数不可能为（）

A、 $2 5^{∘}$ B、 $3 5^{∘}$ C、 $4 5^{∘}$ D、 $5 5^{∘}$

查看试题解析
9. 如图，在△ABC中，AB=AC=10，CB=16，分别以AB、AC为直径作半圆，则图中阴影部分面积是（）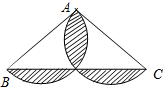

A、50π﹣48 B、25π﹣48 C、50π﹣24 D、 $\frac{25}{2} π - 24$

查看试题解析
10. 如图，撬钉子的工具是一个杠杆，动力臂 $L_{1} = L \cdot \cos α$ ，阻力臂 $L_{2} = l \cdot \cos β$ ，如果动力F的用力方向始终保持竖直向下，当阻力不变时，则杠杆向下运动时的动力变化情况是（）

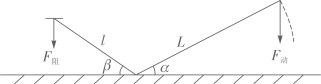A、越来越小 B、不变 C、越来越大 D、无法确定

查看试题解析
11. 构建几何图形解决代数问题是“数形结合”思想的重要性，在计算tan15°时，如图．在Rt△ACB中，∠C＝90°，∠ABC＝30°，延长CB使BD＝AB ，连接AD ，得∠D＝15°，所以tan15° $= \frac{A C}{C D} = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．类比这种方法，计算tan22.5°的值为（　　）

A、 $\sqrt{2} + 1$ B、 $\sqrt{2}$ ﹣1 C、 $\sqrt{2}$ D、 $\frac{1}{2}$

查看试题解析
12. 记实数 $x_{1}$ ， $x_{2}$ ， $\cdot \cdot \cdot$ ， $x_{n}$ 中的最大数为 $m a x {x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{n}}$ ，例如 $m a x {- 2 ， 0 ， 2} = 2$ ，则函数 $y = m a x {- 3 x - 3 ， 2 - x ， x}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 因式分解： $a^{3} - 2 a^{2} + a =$ ．

查看试题解析
14. 如图，点 $E$ 、 $F$ 、 $G$ 分别在正方形 $A B C D$ 的边 $A B$ 、 $B C$ 、 $A D$ 上， $A F ⊥ E G$ ．若 $A B = 6$ ， $A E = D G = 1$ ，则 $B F =$ ．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A C = 6$ ， $B C = 8$ ，点 $D$ 、 $E$ 分别在 $A C$ 、 $B C$ 上，点 $F$ 在 $△ A B C$ 内．若四边形 $C D F E$ 是边长为2的正方形，则 $c o s ∠ A B F =$ ．

查看试题解析
16. 我们规定：若 $\vec{a} = (x_{1} ， y_{1})$ ， $\vec{b} = (x_{2} ， y_{2})$ ，则 $\vec{a} \cdot \vec{b} = x_{1} x_{2} + y_{1} y_{2}$ ．例如 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (3 ， 4)$ ，则 $\vec{a} \cdot \vec{b} = 1 \times 3 + 2 \times 4 = 3 + 8 = 11$ ．已知 $\vec{a} = (x + 1 ， x - 1)$ ， $\vec{b} = (x - 3 ， 4)$ ，且 $- 3 \leq x \leq 2$ ，则 $\vec{a} \cdot \vec{b}$ 的最大值是．

查看试题解析

三、解答题

17. 计算 ${(- 1)}^{2021} + | \sqrt{2} - 3 | - 2 c o s 4 5^{∘} + \sqrt{8}$ ；

查看试题解析
18. 随着科学技术的不断进步，无人机被广泛应用到实际生活中，小霖利用无人机来测量广场 $B$ ， $C$ 两点之间的距离．如图所示，小霖站在广场的 $B$ 处遥控无人机，无人机在 $A$ 处距离地面的飞行高度是41.7m，此时从无人机测得广场 $C$ 处的俯角为 $6 3^{°}$ ，他抬头仰视无人机时，仰角为 $α$ ，若小霖的身高 $B E = 1.7 m$ ， $E A = 50 m$ （点 $A$ ， $E$ ， $B$ ， $C$ 在同一平面内）．

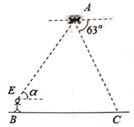(1)、求仰角 $α$ 的正弦值：

(2)、求 $B$ ， $C$ 两点之间的距离（结果精确到 $1 m$ ）．（ $s i n 6 3^{∘} \approx 0.89$ ， $c o s 6 3^{∘} \approx 0.45$ ， $t a n 6 3^{∘} \approx 1.96$ ， $s i n 2 7^{∘} \approx 0.45$ ， $c o s 2 7^{∘} \approx 0.89$ ， $t a n 2 7^{∘} \approx 0.51$ ）

查看试题解析
19. 某学校为了解全校学生对电视节目（新闻、体育、动画、娱乐、戏曲）的喜爱情况，从全校学生中随机抽取部分学生进行问卷调查，并把调查结果绘制成两幅不完整的统计图．
请根据以上信息，解答下列问题

(1)、请将条形统计图补充完整：

(2)、若该校有4000名学生，估计全校学生中喜欢体育节目的约有多少名；

(3)、该校宣传部需要宣传干事，现决定从喜欢新闻节目的 $A$ 、 $B$ 、 $C$ 、 $D$ 四名同学中选取2名，用树状图或列表法求恰好选中 $A$ 、 $D$ 两位同学的概率．

查看试题解析
20. 如图，钝角 $△ A B C$ 中， $A B = A C$ ， $⊙ O$ 为 $△ A B C$ 的外接圆，点 $D$ 为优弧 $\overset{⌢}{B C}$ 上一点（不与 $B$ ， $C$ 重合），连接 $A D$ ， $C D$ ， $A D$ 交 $B C$ 于点 $E$ ， $△ A C D$ 的内心 $F$ 恰好落在 $B C$ 上．

(1)、求证：AB∥CD；

(2)、连接 $A F$ ，求证： $A B = B F$ ；

(3)、若 $B E = 4$ ， $C E = 5$ ，求 $C F$ 的长．

查看试题解析
21. 背景：点A在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上， $A B ⊥ x$ 轴于点B， $A C ⊥ y$ 轴于点C，分别在射线 $A C ， B O$ 上取点 $D ， E$ ，使得四边形 $A B E D$ 为正方形.如图1，点A在第一象限内，当 $A C = 4$ 时，小李测得 $C D = 3$ .
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系.请帮助小李解决下列问题.

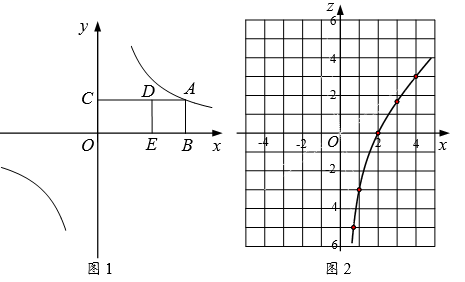(1)、求k的值.

(2)、设点 $A ， D$ 的横坐标分别为 $x ， z$ ，将z关于x的函数称为“Z函数”.如图2，小李画出了 $x > 0$ 时“Z函数”的图象.
①求这个“Z函数”的表达式.

②补画 $x < 0$ 时“Z函数”的图象，并写出这个函数的性质（两条即可）.

③过点 $(3 ， 2)$ 作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标.

查看试题解析
22. 如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线，图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌底部的距离）是1米，当喷射出的水流距离喷灌架水平距离为20米时，达到最大高度11米，现将喷灌架置于坡度为1：10的坡地底部点O处，草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB，因为刚刚被喷洒了农药，近期不能被喷灌．

(1)、求水流运行轨迹满足的函数关系式；

(2)、若将喷灌向后移动5米，通过计算说明是否可避开对这棵石榴树的喷灌？

(3)、设喷射水流与坡面OA之间的铅直高度为h，求h的表达式，并求出x为何值时，h有最大值，h最大值是多少？

查看试题解析
23. 数学实践活动，是一种非常有效的学习方式．通过活动可以激发我们的学习兴趣，提高动手动脑能力，拓展思推空间，丰富数学体验．让我们一起动手来折一折、转一转、剪一剪，体会活动带给我们的乐趣．
折一折：将正方形纸片 $A B C D$ 折叠，使边 $A B$ 、 $A D$ 都落在对角线 $A C$ 上，展开得折痕 $A M$ 、 $A N$ ，连接 $M N$ ，如图1．
转一转：将图1中的 $∠ M A N$ 绕点 $A$ 旋转，使它的两边分别交边 $B C$ 、 $C D$ 于点 $E$ 、 $F$ ，连接 $E F$ ，如图2．
剪一剪：将图3中的正方形纸片沿对角线 $B D$ 剪开，如图4．

(1)、 $∠ M A N$ $^{∘}$ ，写出图中两个等腰三角形：（不需要添加字母）；

(2)、线段 $B E$ 、 $E F$ 、 $D F$ 之间的数量关系为；

(3)、连接正方形对角线 $B D$ ，若图2中的 $∠ E A F$ 的边 $A E$ 、 $A F$ 分别交对角线 $B D$ 于点 $G$ 、点 $H$ ．如图3，求 $\frac{C F}{B G}$ 的值；

(4)、求证： $G H^{2} = B G^{2} + D H^{2}$ ．

查看试题解析