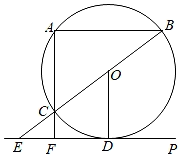山东省聊城市阳谷县2022年中考一模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

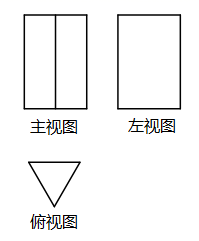
1. 以下各数是有理数的是（）

A、 $\sqrt{2}$ B、 $\sqrt[3]{5}$ C、 $\frac{2}{7}$ D、π

查看试题解析
2. 如图，根据三视图，这个立体图形的名称是（）

A、三棱柱 B、圆柱 C、三棱锥 D、圆锥

查看试题解析
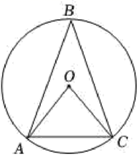
3. 如图，AM∥BN ， ∠ACB＝90°，∠MAC＝35°，则∠CBN的度数是（）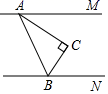

A、35° B、45° C、55° D、65°

查看试题解析
4. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a^{3})}^{2} = a^{5}$ C、 ${(0.1)}^{- 3} = 1000$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
5. 若一组数据1，3，4，6，m的平均数为4，则这组数据的中位数和众数分别是（）

A、4，6 B、4，4 C、3，6 D、3，4

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{12} =$ 3 $\sqrt{2}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\frac{\sqrt{6}}{2} = \sqrt{3}$ D、（ $\sqrt{2}$ ）²＝2

查看试题解析
7. 在 $△ A B C$ 中， $∠ A B C = 90 °$ ，若 $A C = 100 ， \sin A = \frac{3}{5}$ ，则 $A B$ 的长是（）

A、 $\frac{500}{3}$ B、 $\frac{503}{5}$ C、60 D、80

查看试题解析
8. 用配方法解一元二次方程 $2 x^{2} - 3 x - 1 = 0$ ，配方正确的是（）．

A、 ${(x - \frac{3}{4})}^{2} = \frac{17}{16}$ B、 ${(x - \frac{3}{4})}^{2} = \frac{1}{2}$ C、 ${(x - \frac{3}{2})}^{2} = \frac{13}{4}$ D、 ${(x - \frac{3}{2})}^{2} = \frac{11}{4}$

查看试题解析
9. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形， $A B = 2 \sqrt{3}$ ， $∠ A C B = 60 °$ ，连接 $O A$ ， $O B$ ，则 $\overset{⌢}{A B}$ 的长是（）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、π D、 $\frac{4 π}{3}$

查看试题解析
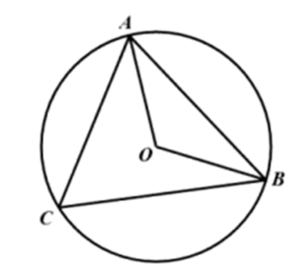10. 设圆锥的底面圆半径为r，圆锥的母线长为l，满足2r+l＝6，这样的圆锥的侧面积（）

A、有最大值 $\frac{9}{4}$ π B、有最小值 $\frac{9}{4}$ π C、有最大值 $\frac{9}{2}$ π D、有最小值 $\frac{9}{2}$ π

查看试题解析
11. 在平面直角坐标系中，已知函数y₁=x²+ax+1，y₂=x²+bx+2，y₃=x²+cx+4，其中a，b，c是正实数，且满足b²=ac。设函数y₁ ， y₂ ， y₃的图象与x轴的交点个数分别为M₁ ， M₂ ， M₃ ，（）

A、若M₁=2，M₂=2，则M₃=0 B、若M₁=1，M₂=0，则M₃=0 C、若M₁=0，M₂=2，则M₃=0 D、若M₁=0，M₂=0，则M₃=0

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以该三角形的三条边为边向形外作正方形，正方形的顶点 $E ， F ， G ， H ， M ， N$ 都在同一个圆上.记该圆面积为 $S_{1}$ ， $△ A B C$ 面积为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 的值是（）

A、 $\frac{5 π}{2}$ B、 $3 π$ C、 $5 π$ D、 $\frac{11 π}{2}$

查看试题解析

二、填空题

13. 分解因式： $3 a^{2} + 12 a + 12 =$ ．

查看试题解析
14. 如图， $A$ ， $B$ ， $C$ 是 $⊙ O$ 上的三个点， $∠ B = 40 °$ ，则 $∠ O A C$ 的度数为.

查看试题解析
15. 若 $x^{2} + x - 1 = 0$ ，则 $3 x - \frac{3}{x} =$ ．

查看试题解析
16. 如图所示的电路图中，当随机闭合 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ 中的两个开关时，能够让灯泡发光的概率为．

查看试题解析
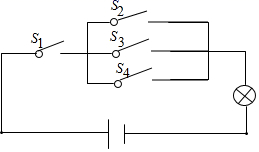17. 如图，在菱形ABCD中， $B C = 2$ ， $∠ C = 120 °$ ，Q为AB的中点，P为对角线BD上的任意一点，则 $A P + P Q$ 的最小值为.

查看试题解析

三、解答题

18. 先化简，再求值：（ $\frac{x}{x - 2}$ ＋1）÷ $\frac{2 x^{2} - 2 x}{x^{2} - 4}$ ，其中x＝tan60°．

查看试题解析
19. 2021年，“碳中和、碳达峰”成为高频热词.为了解学生对“碳中和、碳达峰”知识的知晓情况，某校团委随机对该校九年级部分学生进行了问卷调查，调查结果共分成四个类别：A表示“从未听说过”，B表示“不太了解”，C表示“比较了解”，D表示“非常了解”.根据调查统计结果，绘制成两种不完整的统计图.请结合统计图，回答下列问题.

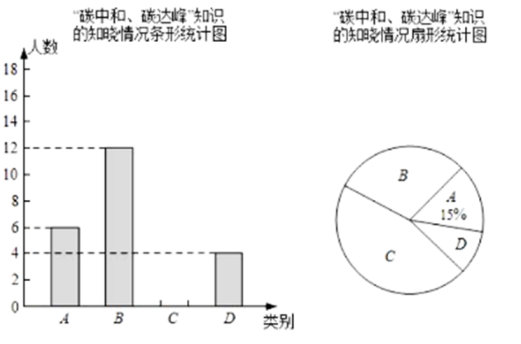(1)、参加这次调查的学生总人数为人；

(2)、扇形统计图中，B部分扇形所对应的圆心角是；

(3)、将条形统计图补充完整；

(4)、在D类的学生中，有2名男生和2名女生，现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员，请利用画树状图或列表的方法，求所抽取的2名学生恰好是1名男生和1名女生的概率.

查看试题解析
20. 《九章算术》被历代数学家尊为“算经之首”.下面是其卷中记载的关于“盈不足”的一个问题：今有共买金，人出四百，盈三千四百；人出三百，盈一百.问人数、金价各几何？这段话的意思是：今有人合伙买金，每人出400钱，会剩余3400钱；每人出300钱，会剩余100钱.合伙人数、金价各是多少？请解决上述问题.

查看试题解析
21. 如图，点 $E$ ， $F$ 分别在正方形 $A B C D$ 的边 $A B$ ， $A D$ 上，且 $A E = D F$ ，点 $G$ ， $H$ 分别在边 $A B$ ， $B C$ 上，且 $F G ⊥ E H$ ，垂足为 $P$ ．

(1)、求证： $F G = E H$ ；

(2)、若正方形 $A B C D$ 边长为5， $A E = 2$ ， $t a n ∠ A G F = \frac{3}{4}$ ，求 $P F$ 的长度．

查看试题解析
22. 如图，为了测量某建筑物CD的高度，在地面上取A，B两点，使A、B、D三点在同一条直线上，拉姆同学在点A处测得该建筑物顶部C的仰角为30°，小明同学在点B处测得该建筑物顶部C的仰角为45°，且AB＝10m.求建筑物CD的高度.（拉姆和小明同学的身高忽略不计.结果精确到0.1m， $\sqrt{3}$ ≈1.732）

查看试题解析
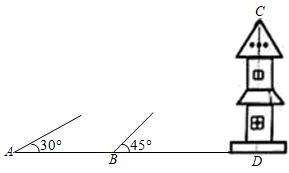23. 如图，一次函数 $y = k_{1} x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图像相交于 $A (1 ， 2)$ 、 $B (- 2 ， n)$ 两点．

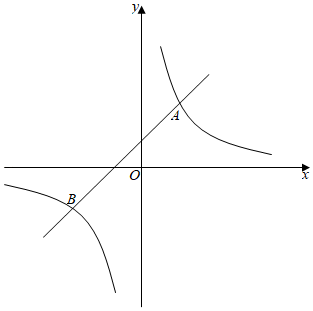(1)、求一次函数和反比例函数的解析式；

(2)、根据图象，直接写出满足 $k_{1} x + b > \frac{k_{2}}{x}$ 的 $x$ 的取值范围；

(3)、若点 $P$ 在线段 $A B$ 上，且 $S_{Δ A O P} ： S_{Δ B O P} = 1 ： 4$ ，求点 $P$ 的坐标．

查看试题解析
24. 如图，DP是⊙O的切线，D为切点，弦AB $/ /$ DP，连接BO并延长，与⊙O交于点C，与DP交于点E，连接AC并延长，与DP交于点F，连接OD．

(1)、求证：AF $/ /$ OD；

(2)、若OD＝5，AB＝8，求线段EF的长．

查看试题解析
25. 已知O为坐标原点，直线l：y＝﹣ $\frac{1}{2}$ x＋2与x轴、y轴分别交于A、C两点，点B（4，2）关于直线l的对称点是点E，连接EC交x轴于点D.

(1)、求证：AD＝CD；

(2)、求经过B、C、D三点的抛物线的函数表达式；

(3)、当x＞0时，抛物线上是否存在点P，使S_△PBC＝ $\frac{5}{3}$ S_△OAE？若存在，求点P的坐标；若不存在，说明理由.

查看试题解析