山东省聊城市高唐县2022年中考二模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列各数:0.456, , , 0.1010010001…(相邻两个1之间0的个数逐次加1), , , , 其中是无理数的有( )A、2个 B、3个 C、4个 D、5个2. 某自动控制器的芯片,可植入2020000000粒晶体管,这个数字2020000000用科学记数法可表示为( )A、 B、 C、 D、3. 如图,下列关于物体的主视图画法正确的是( )
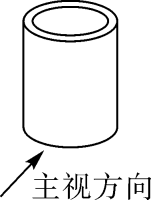 A、
A、 B、
B、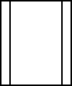 C、
C、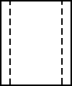 D、
D、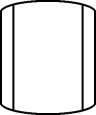 4. 下列说法正确的是( )A、为了了解全国中学生的心理健康情况,选择全面调查 B、在一组数据7,6,5,6,6,4,8中,众数和中位数都是6 C、“若 是实数,则 ”是必然事件 D、若甲组数据的方差 ,乙组数据的方差 ,则乙组数据比甲组数据稳定5. 将一副直角三角尺按如图所示的方式摆放在一起,其中 , , ,点 在边 上, , 分别交 于点 , .若 ,则 的度数为( )
4. 下列说法正确的是( )A、为了了解全国中学生的心理健康情况,选择全面调查 B、在一组数据7,6,5,6,6,4,8中,众数和中位数都是6 C、“若 是实数,则 ”是必然事件 D、若甲组数据的方差 ,乙组数据的方差 ,则乙组数据比甲组数据稳定5. 将一副直角三角尺按如图所示的方式摆放在一起,其中 , , ,点 在边 上, , 分别交 于点 , .若 ,则 的度数为( )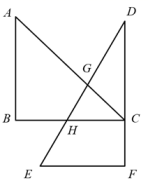 A、 B、 C、 D、6. 如图,在中,DE垂直平分BC,若 , 则的度数为( )
A、 B、 C、 D、6. 如图,在中,DE垂直平分BC,若 , 则的度数为( ) A、 B、 C、 D、7. 如图,等腰的顶角为 , 以腰AB为直径作半圆,交BC于点D,交AC于点E,则的度数为( )
A、 B、 C、 D、7. 如图,等腰的顶角为 , 以腰AB为直径作半圆,交BC于点D,交AC于点E,则的度数为( ) A、25 B、35 C、50 D、658. 如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=( )
A、25 B、35 C、50 D、658. 如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=( ) A、 B、 C、3 D、69. 如图,中, , 点分别是边的中点依次以为圆心长为半径画弧得到 . 若在区域随机任取一点,则该点取自阴影部分的概率是( )
A、 B、 C、3 D、69. 如图,中, , 点分别是边的中点依次以为圆心长为半径画弧得到 . 若在区域随机任取一点,则该点取自阴影部分的概率是( )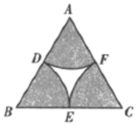 A、 B、 C、 D、10. 如图,在菱形中, , 的垂直平分线交对角线于点 , 垂足为 . 连接 , 则等于( )
A、 B、 C、 D、10. 如图,在菱形中, , 的垂直平分线交对角线于点 , 垂足为 . 连接 , 则等于( ) A、 B、 C、 D、11. 如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线 对折,点O恰好落在∠OAB的平分线上的O’处,则b的值为( )
A、 B、 C、 D、11. 如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线 对折,点O恰好落在∠OAB的平分线上的O’处,则b的值为( )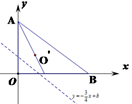 A、 B、 C、 D、12. 如图,的直径AB垂直于弦CD,垂足为E,P为上一个动点,点P沿在半圆上运动(点P不与点A重合),AP交CD所在的直线于点F若 , 记 , 则y关于x的函数图象大致是( )
A、 B、 C、 D、12. 如图,的直径AB垂直于弦CD,垂足为E,P为上一个动点,点P沿在半圆上运动(点P不与点A重合),AP交CD所在的直线于点F若 , 记 , 则y关于x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 五一期间,时代商场开展打折促销活动,某商品如果按原售价的八折出售,将盈利20元,而按原售价的六折出售,将亏损60元,则该商品的原售价为 .14. 在如图方格中,若要使横、竖、斜对角的3个实数相乘都得到同样的结果,则2个空格的实数之积为 .
2
1
6
3
15. 如图,四边形ABCO为平行四边形,A,C两点的坐标分别是(3,0) ,(1,2),则平行四边形ABCO的周长等于 . 16. 如图①,E为矩形ABCD的边AD上一点,点P从点B出发沿折线B-E-D运动到点D停止,点Q从点B出发沿BC运动到点C停止,它们的运动速度都是 . 现P,Q两点同时出发,设运动时间为 , 的面积为 , 若y与x的对应关系如图②所示,则矩形ABCD的面积是 .
16. 如图①,E为矩形ABCD的边AD上一点,点P从点B出发沿折线B-E-D运动到点D停止,点Q从点B出发沿BC运动到点C停止,它们的运动速度都是 . 现P,Q两点同时出发,设运动时间为 , 的面积为 , 若y与x的对应关系如图②所示,则矩形ABCD的面积是 . 17. 如果实数a,b满足的形式,那么a和b就是“智慧数”,用表示.如:由于 , 所以是“智慧数”,现给出以下结论:①和是“智慧数”;②如果(3,☆)是“智慧数”,那么“☆”的值为;③如果是“智慧数”,则y与x之间的关系式为;④如果是“智慧数”,当时,y随x的增大而增大,其中正确的是 . (写出所有正确结论的序号)
17. 如果实数a,b满足的形式,那么a和b就是“智慧数”,用表示.如:由于 , 所以是“智慧数”,现给出以下结论:①和是“智慧数”;②如果(3,☆)是“智慧数”,那么“☆”的值为;③如果是“智慧数”,则y与x之间的关系式为;④如果是“智慧数”,当时,y随x的增大而增大,其中正确的是 . (写出所有正确结论的序号)三、解答题
-
18. 若数a使关于x的分式方程的解为非负数,且使关于y的不等式组的解集为 , 求符合条件的所有整数a的积.19. 2022北京冬奥会和冬残奥会顺利闭幕,吸引了世界各地冬奥选手参加.现对某校初中1000名学生就“高山跳台滑雪比赛”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制出两幅不完整的统计图表,请根据统计图表回答下列问题:
类别
频数
频率
不了解
10
m
了解很少
16
0.32
基本了解
b
很了解
4
n
合计
a
1
 (1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全校举办的“高山跳台滑雪比赛”知识竞赛决赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.20. 在期末一节复习课上,八年(一)班的数学老师要求同学们列二元一次方程组解下列问题:
(1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全校举办的“高山跳台滑雪比赛”知识竞赛决赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.20. 在期末一节复习课上,八年(一)班的数学老师要求同学们列二元一次方程组解下列问题:在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建的村路,甲队每天修建 , 乙队每天修建 , 共用18天完成.
(1)、粗心的张红同学,根据题意,列出的两个二元一次方程,等号后面忘记写数据,得到了个不完整的二元一次方程组张红列出的这个不完整的方程组中未知数表示的是 , 未知数表示的是;张红所列出正确的方程组应该是;(2)、李芳同学的思路是想设甲工程队修建了村路,乙工程队修建了村路.下面请你按照李芳的思路,求甲、乙两个工程队分别修建了多少天?21. 已知是等边三角形,点D为平面内一点,连接DB,DC, . 如图①,当点D在BC下方时,连接AD,延长DC到点E,使 , 连接AE. (1)、求证:;(2)、如图②,过点A作于点F,求线段AF,BD,DC间的数量关系.22. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .
(1)、求证:;(2)、如图②,过点A作于点F,求线段AF,BD,DC间的数量关系.22. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .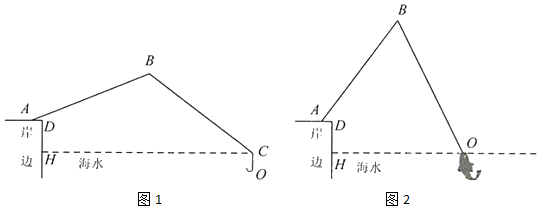 (1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )23. 如图,在菱形ABCD中,对角线AC,BD交于点O, , . 过点O作于点H,以点O为圆心,OH为半径的半圆交AC于点M.
(1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )23. 如图,在菱形ABCD中,对角线AC,BD交于点O, , . 过点O作于点H,以点O为圆心,OH为半径的半圆交AC于点M. (1)、求图中阴影部分的面积;(2)、点P是BD上的一个动点(点P不与点B,D重合),当的值最小时,求PD的长度.24. 背景:点A在反比例函数()的图象上,轴于点B,轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形,如图1,点A在第一象限内,当时,小李测得 .
(1)、求图中阴影部分的面积;(2)、点P是BD上的一个动点(点P不与点B,D重合),当的值最小时,求PD的长度.24. 背景:点A在反比例函数()的图象上,轴于点B,轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形,如图1,点A在第一象限内,当时,小李测得 .探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系,请帮助小李解决下列问题.
 (1)、求k的值;(2)、设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了时“Z函数”的图象.
(1)、求k的值;(2)、设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了时“Z函数”的图象.①求这个“Z函数”的表达式.
②过点作一直线,与这个“Z函数”图象仅有一个交点,求该交点的横坐标.
25. 如图,抛物线 经过点 , ,直线AC的解析式为 ,且与y轴相交于点C,若点E是直线AB上的一个动点,过点E作 轴交AC于点F. (1)、求抛物线 的解析式;(2)、点H是y轴上一动点,连结EH,HF,当点E运动到什么位置时,四边形EAFH是矩形?求出此时点E,H的坐标;(3)、在(2)的前提下,以点E为圆心,EH长为半径作圆,点M为 上以动点,求 的最小值.
(1)、求抛物线 的解析式;(2)、点H是y轴上一动点,连结EH,HF,当点E运动到什么位置时,四边形EAFH是矩形?求出此时点E,H的坐标;(3)、在(2)的前提下,以点E为圆心,EH长为半径作圆,点M为 上以动点,求 的最小值.