山东省聊城市东昌府区2022年中考二模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
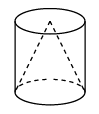
1. 下列各数:3.1415926, , , , 其中是无理数的是( )A、3.1415926 B、 C、 D、2. 如图,一个圆柱体内部挖去一个圆锥,其左视图是( )
 A、
A、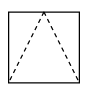 B、
B、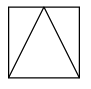 C、
C、 D、
D、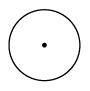 3. 下列调查工作需采用普查方式的是( )A、环保部门对流经我市徒骇河水域的水污染情况的调查 B、我市教育部门对疫情期间学生线上上课情况的调查 C、质检部门对各厂家生产的电池使用寿命的调查 D、学校在订购学生校服前进行的尺寸大小的调查4. 如图,已知 , 含有角的直角三角板的直角顶点在直线a上,若 , 则等于( )
3. 下列调查工作需采用普查方式的是( )A、环保部门对流经我市徒骇河水域的水污染情况的调查 B、我市教育部门对疫情期间学生线上上课情况的调查 C、质检部门对各厂家生产的电池使用寿命的调查 D、学校在订购学生校服前进行的尺寸大小的调查4. 如图,已知 , 含有角的直角三角板的直角顶点在直线a上,若 , 则等于( ) A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 下列二次根式的运算正确的是( )A、 B、 C、 D、7. 在平面直角坐标系中,点A的坐标为 , 以原点O为中心,将点A顺时针旋转得到点 , 则点坐标为( )A、 B、 C、 D、8. 已知圆锥的底面积为 , 高为 , 则圆锥的侧面积是( )A、 B、 C、 D、9. 若关于x的一元一次不等式组无解,则m的取值范围是( )A、 B、 C、 D、10. 如图,是的直径, , 分别位于直径的上下两侧,连接 , , 若 , 则的度数为( )
A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 下列二次根式的运算正确的是( )A、 B、 C、 D、7. 在平面直角坐标系中,点A的坐标为 , 以原点O为中心,将点A顺时针旋转得到点 , 则点坐标为( )A、 B、 C、 D、8. 已知圆锥的底面积为 , 高为 , 则圆锥的侧面积是( )A、 B、 C、 D、9. 若关于x的一元一次不等式组无解,则m的取值范围是( )A、 B、 C、 D、10. 如图,是的直径, , 分别位于直径的上下两侧,连接 , , 若 , 则的度数为( ) A、 B、 C、 D、11. 如图,中, , , , 将绕点B逆时针旋转得 , 若点在上,连接 , 则的长为( )
A、 B、 C、 D、11. 如图,中, , , , 将绕点B逆时针旋转得 , 若点在上,连接 , 则的长为( ) A、 B、 C、 D、12. 如图,点P,Q从边长为2的等边三角形的点B出发,分别沿着 , 两边以相同的速度在的边上运动,当两点在边上运动到重合时停止.在此过程中,设点P,Q移动过程中各自的路程为x,所得的面积为y,则y随x变化的函数图象大致为( )
A、 B、 C、 D、12. 如图,点P,Q从边长为2的等边三角形的点B出发,分别沿着 , 两边以相同的速度在的边上运动,当两点在边上运动到重合时停止.在此过程中,设点P,Q移动过程中各自的路程为x,所得的面积为y,则y随x变化的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 若关于的方程不存在实数根,则的取值范围是 .14. 因式分解: .15. 小莹一次随机从两个分别放有四个编号为1、2、3、4且形状质量相同小球的盒子中摸出两个小球,将两球编号数相加得到一个和,其中得到某个和的概率最大,则这个概率是 .16. 如图,在矩形中,M为边上一点,连接 , 将沿翻折使得C点恰好落在上的点处,若 , , 则的长为 .
 17. 观察给出的一列数: , …,根据其中的规律,那么第n个(用含n的式子表示).
17. 观察给出的一列数: , …,根据其中的规律,那么第n个(用含n的式子表示).三、解答题
-
18. 化简并求值: , 其中 .19. 我市农科院培育了A,B两个新品种的桃树,在口感相同的情况下,农科院希望选育出个大品相好的品种.科研人员从两个品种的桃树上分别抽取了100个桃子,然后再分别从中随机抽取了10个桃子,记录了它们的质量(单位:克)如下:
A加工厂
74
75
75
75
73
77
78
72
76
75
B加工厂
78
74
78
75
73
75
74
75
75
75
(1)、根据表中数据,可得10个A品种桃子质量的中位数、众数、平均数都是75,求10个B品种桃子质量的中位数、众数、平均数分别是多少?(2)、在(1)的条件下,农科院可选育哪个品种的桃子?说出你的理由.(3)、估计这100个B品种桃子中,质量为75克的桃子有多少个?(4)、根据表中数据可得A,B桃子质量的方差分别为 , 根据桃子质量的稳定性,农科院应选育哪个品种的桃子?20. 如图所示,在中,E,F分别为边 , 的中点,连接 , , , 作 , 交的延长线于点G,连接 . (1)、求证:四边形是平行四边形;(2)、当平分时,求证:四边形是矩形.21. 某品牌时装店四月份购进甲、乙两种时装共花费1.7万元,其中甲时装80元/件,乙时装180元/件,由于热销,五月份再购进时两种时装涨价,此时甲时装100元/件,乙时装200元/件.(1)、若五月份购进两种时装的数量分别与四月份相同,将多支付3000元,求四月份购进这两种时装分别是多少件?(2)、若五月份将这两种时装进货总量减少到120件,且甲时装不超过乙时装的3倍,则五月份时装店需要支付这两种时装的货款最少应是多少元?22. 美丽的东昌湖是我市的一大旅游胜地.如图,湖岸的一段长40米,与桥所在的路线成的角,小亮在B点处测得与桥的夹角 , 在点A处测得与平行于桥的直线之间的夹角为 , 桥与湖岸是垂直的.求湖岸上的路线的长.(结果保留根号)
(1)、求证:四边形是平行四边形;(2)、当平分时,求证:四边形是矩形.21. 某品牌时装店四月份购进甲、乙两种时装共花费1.7万元,其中甲时装80元/件,乙时装180元/件,由于热销,五月份再购进时两种时装涨价,此时甲时装100元/件,乙时装200元/件.(1)、若五月份购进两种时装的数量分别与四月份相同,将多支付3000元,求四月份购进这两种时装分别是多少件?(2)、若五月份将这两种时装进货总量减少到120件,且甲时装不超过乙时装的3倍,则五月份时装店需要支付这两种时装的货款最少应是多少元?22. 美丽的东昌湖是我市的一大旅游胜地.如图,湖岸的一段长40米,与桥所在的路线成的角,小亮在B点处测得与桥的夹角 , 在点A处测得与平行于桥的直线之间的夹角为 , 桥与湖岸是垂直的.求湖岸上的路线的长.(结果保留根号) 23. 图,已知点A是反比例函数的一支图象上的一点,过点A作轴分别交x轴于点C,交反比例函数的图象的一支于点 , 连接 , 有 , 若的面积为 .
23. 图,已知点A是反比例函数的一支图象上的一点,过点A作轴分别交x轴于点C,交反比例函数的图象的一支于点 , 连接 , 有 , 若的面积为 . (1)、求n的值;(2)、求反比例函数的解析式.
(1)、求n的值;(2)、求反比例函数的解析式.

