山东省聊城市茌平区2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. -2的倒数是( )A、-2 B、 C、 D、22. 清代袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、 B、 C、 D、3. 如图, 平分 ,若 ,则 的度数为( )
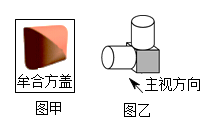
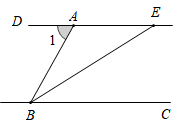 A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是()
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是()
 A、
A、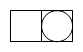
B、
B、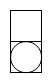
C、
C、
D、
D、
6. 解不等式组 时,不等式①②的解集在同一数轴上表示正确的是( )A、
6. 解不等式组 时,不等式①②的解集在同一数轴上表示正确的是( )A、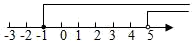 B、
B、 C、
C、 D、
D、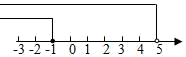 7. 已知a是方程的一个根,则代数式的值为( )A、1 B、 C、或1 D、28. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边BC为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
7. 已知a是方程的一个根,则代数式的值为( )A、1 B、 C、或1 D、28. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边BC为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( ) A、2 B、3 C、4 D、59. 二次函数的图象如图所示,则一次函数的图象大致是( )
A、2 B、3 C、4 D、59. 二次函数的图象如图所示,则一次函数的图象大致是( ) A、
A、 B、
B、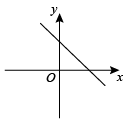 C、
C、 D、
D、 10. 如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,⊙O的半径为 ,则弦CD的长为( )
10. 如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,⊙O的半径为 ,则弦CD的长为( )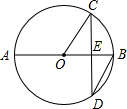 A、 B、3cm C、 D、9cm11. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A、 B、3cm C、 D、9cm11. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )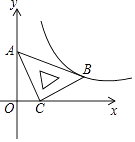 A、( ,0) B、(2,0) C、( ,0) D、(3,0)12. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )
A、( ,0) B、(2,0) C、( ,0) D、(3,0)12. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )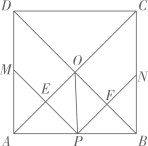 A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤
A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤二、填空题
-
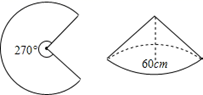
13. 计算:= .14. 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是cm.
 15. 将写有“北”“京”“冬”“奥”“会”汉字的五张除汉字外都相同的卡片放入一个不透明的袋子里,每次摸之前先均匀搅拌,随机摸出一张卡片,不放回,再随机摸出一张卡片,两次摸出卡片上的汉字能组成“北京”的概率是 .16. 关于的一元二次方程有两个不相等的实数根,则的取值范围是 .17. 如图,在直角坐标系中,的圆心A的坐标为(1,0),半径为1,点P为直线上的动点,过点P作的切线,切点为Q,则切线长PQ的最小值是 .
15. 将写有“北”“京”“冬”“奥”“会”汉字的五张除汉字外都相同的卡片放入一个不透明的袋子里,每次摸之前先均匀搅拌,随机摸出一张卡片,不放回,再随机摸出一张卡片,两次摸出卡片上的汉字能组成“北京”的概率是 .16. 关于的一元二次方程有两个不相等的实数根,则的取值范围是 .17. 如图,在直角坐标系中,的圆心A的坐标为(1,0),半径为1,点P为直线上的动点,过点P作的切线,切点为Q,则切线长PQ的最小值是 .
三、解答题
-
18. 先化简,再求值: , 其中 .19. 疫情期间某校学生积极观看网络直播课程,为了了解全校500名学生观看网络直播课程的情况,随机抽取50名学生,对他们观看网络直播课程的节数进行收集,并对数据进行了整理、描述和分析,下面给出了部分信息.
观看直播课节数的频数分布表
节数x
频数
频率
8
0.16
10
0.20
16
0.24
4
0.08
总数
50
1
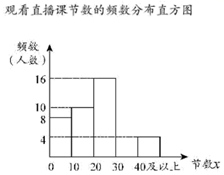
其中,节数在 这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)、 , ;(2)、请补全频数分布直方图;(3)、随机抽取的50名学生观看直播课节数的中位数是;(4)、请估计该校学生中观看网络直播课节数不低于30次的约有人.20. 我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买A,B两种奖品.已知2件A种奖品和3件B种奖品共需41元,5件A种奖品和2件B种奖品共需53元.(1)、这两种奖品的单价各是多少元?(2)、学校准备购进这两种奖品共90件,且B种奖品的数量不少于A种奖品数量的 , 请设计出最省钱的购买方案,并求出最少费用.21. 如图,在中,为边的中点,连接并延长,交的延长线于点 , 延长至点 , 使 , 分别连接 , , .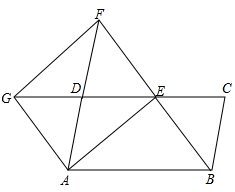 (1)、求证:;(2)、当平分时,四边形是什么特殊四边形?请说明理由.22. 如图,某河堤下有一棵与水平面垂直的树AB,小明准备测量它的高度,已知斜坡BC的坡度为1:2,小明选择在河堤的C和D处测量(A,B,C,D在同一平面内),测角仪CE和DF高度均为1.5米,C处测得树顶端A的仰角为45°,D处测得树顶端A的仰角为37°,C,D两点间的距离为3.5米,求树AB的高度.(精确到0.1米.参考数据: , , , )
(1)、求证:;(2)、当平分时,四边形是什么特殊四边形?请说明理由.22. 如图,某河堤下有一棵与水平面垂直的树AB,小明准备测量它的高度,已知斜坡BC的坡度为1:2,小明选择在河堤的C和D处测量(A,B,C,D在同一平面内),测角仪CE和DF高度均为1.5米,C处测得树顶端A的仰角为45°,D处测得树顶端A的仰角为37°,C,D两点间的距离为3.5米,求树AB的高度.(精确到0.1米.参考数据: , , , ) 23. 已知:如图,矩形ABCD的BC边在x轴上, , , E是DC的中点,反比例函数的图象经过点E,与AB交于点F.
23. 已知:如图,矩形ABCD的BC边在x轴上, , , E是DC的中点,反比例函数的图象经过点E,与AB交于点F. (1)、若点B的坐标为 , 求这个反比例函数的表达式和过A,E两点的一次函数表达式;(2)、若 , 求这个反比例函数的表达式.
(1)、若点B的坐标为 , 求这个反比例函数的表达式和过A,E两点的一次函数表达式;(2)、若 , 求这个反比例函数的表达式.

