山东省济宁市任城区2022年九年级中考二模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，最小的数是（）

A、0 B、﹣2 C、1 D、﹣ $\sqrt{3}$

查看试题解析
2. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
3. 随着北斗系统全球组网的步伐，北斗芯片的研发生产技术也在逐步成熟，国产北斗芯片可支持接收多系统的导航信号，应用于自动驾驶、无人机、机器人等高精度定位需求领域，将为中国北斗导航产业发展提供有力支持．目前，该芯片工艺已达22纳米（即0.000000022米）．则数据0.000000022用科学记数法表示为（）

A、 $0.22 \times 1 0^{- 7}$ B、 $22 \times 1 0^{- 9}$ C、 $2.2 \times 1 0^{- 8}$ D、 $2.2 \times 1 0^{- 9}$

查看试题解析
4. 如图，该几何体的左视图是（）

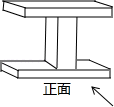A、 B、 C、 D、

查看试题解析
5. 下列二次根式能与 $2 \sqrt{2}$ 合并的是（）

A、 $\sqrt{12}$ B、 $\sqrt{24}$ C、 $\sqrt{8}$ D、 $\sqrt{6}$

查看试题解析
6. 某商户开展抽奖活动，如图所示的两个转盘分别被均匀地分成5个和4个扇形．每个扇形上都标有数字，当满足抽奖条件的某个客户同时自由转动两个转盘则转盘停止后，指针都落在偶数上（指针落在线上时，重新转动转盘）的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{1}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{2}$

查看试题解析
7. 如图，一张长方形桌子的桌面长130 cm，宽 60 cm，一块长方形台布的面积是桌面面积的1.5倍，并且铺在桌面上时，各边垂下的长度相等．设台布垂下的长度为 $x$ cm，则根据题意可列方程（）

A、 $(130 - x) (60 - x) = 130 \times 60 \times 1.5$ B、 $(130 + x) (60 + x) = 130 \times 60 \times 1.5$ C、 $(130 - 2 x) (60 - 2 x) = 130 \times 60 \times 1.5$ D、 $(130 + 2 x) (60 + 2 x) = 130 \times 60 \times 1.5$

查看试题解析
8. 如图，五边形ABCDE是正五边形， $A F ∥ D G$ ，若 $∠ 2 = 20 °$ ，则 $∠ 1 =$ （）

A、60° B、56° C、52° D、40°

查看试题解析
9. 如图， $∠ M O N = 30 °$ ，在 $O M$ 上截取 $O A_{1} = \sqrt{3}$ ．过点 $A_{1}$ 作 $A_{1} B_{1} ⊥ O M$ ，交 $O N$ 于点 $B_{1}$ ，以点 $B_{1}$ 为圆心， $B_{1} O$ 为半径画弧，交 $O M$ 于点 $A_{2}$ ；过点 $A_{2}$ 作 $A_{2} B_{2} ⊥ O M$ ，交 $O N$ 于点 $B_{2}$ ，以点 $B_{2}$ 为圆心， $B_{2} O$ 为半径画弧，交 $O M$ 于点 $A_{3}$ ；按此规律，所得线段 $A_{2022} B_{2022}$ 的长等于（）

A、 $2^{2021}$ B、 $2^{2020}$ C、 $2^{2023}$ D、 $2^{2022}$

查看试题解析
10. 在矩形ABCD中，AB=3，AD=5，将矩形ABCD绕点A沿逆时针方向旋转得矩形AEFG，连接BE，当EF刚好经过点D时，线段BE的长是（）

A、 $\frac{3}{5} \sqrt{7}$ B、 $\frac{3}{5} \sqrt{10}$ C、 $\frac{3}{5} \sqrt{11}$ D、 $\frac{3}{5} \sqrt{13}$

查看试题解析

二、填空题

11. 设 $x_{1} ， x_{2}$ 是一元二次方程 $x^{2} - 2 x - 1 = 0$ 的两根，则 $x_{1} + x_{2} + x_{1} x_{2} =$ ．

查看试题解析
12. 如图，将 $△ A B D$ 沿 $△ A B C$ 的角平分线 $A D$ 所在直线翻折，点B在 $A C$ 边上的落点记为点E．已知 $∠ C = 20 °$ ， $A B + B D = A C$ ，那么 $∠ B$ 等于．

查看试题解析
13. 如果 $m^{2} + m = 3$ ，那么代数式 $m (m - 2) + (m + 2)^{2}$ 的值为．

查看试题解析
14. 如图， $R t △ A B C$ 中， $∠ C = 90 ° ， ∠ A = 30 ° ， B C = \sqrt{3}$ ，以点B为圆心，以 $B C$ 长度为半径作弧，交 $B A$ 于点D，分别以点C，D为圆心，以大于 $\frac{1}{2} C D$ 为半径作弧，两弧交于点E，作射线 $B E$ 交 $C A$ 于点F，以点B为圆心，以 $B F$ 为长度作弧，交 $B A$ 于点G，则阴影部分的面积为．

查看试题解析
15. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = k_{1} x + 4$ 与y轴交于点C，与反比例函数 $y = \frac{k_{2}}{x}$ 在第一象限内的图象交于点B，连接 $B O$ ，若 $S_{△ O B C} = 2$ ， $t a n ∠ B O C = \frac{1}{5}$ ，则 $k_{2}$ 的值是．

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{1}{x + 1} - 1) \div \frac{x^{2} - x}{x + 1}$ ，其中x是﹣1、1、2中的一个合适的数．

查看试题解析
17. 国家规定“中小学生每天在校体育活动时间不低于 $1 h$ ”．为此，某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生，根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：
A组： $t < 0.5 h$ B组： $0.5 h \leq t < 1 h$ C组： $1 h \leq t < 1.5 h$ D组： $t \geq 1.5 h$
请根据上述信息解答下列问题：

(1)、本次调查的人数是人；

(2)、请根据题中的信息补全频数分布直方图；

(3)、D组对应扇形的圆心角为 $°$ ；

(4)、本次调查数据的中位数落在组内．

查看试题解析
18. 如图，在 $△ A B C$ 中， $B A = B C$ ， $B D$ 平分 $∠ A B C$ 交 $A C$ 于点D，点E在线段 $B D$ 上，点F在 $B D$ 的延长线上，且 $D E = D F$ ，连接 $A E$ ， $C E$ ， $A F$ ， $C F$ ．

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、若 $B A ⊥ A F$ ， $A D = 4$ ， $B C = 4 \sqrt{5}$ ，求 $B D$ 和 $A E$ 的长．

查看试题解析
19. A，B两地相距200千米．早上8：00货车甲从A地出发将一批物资运往B地，行驶一段路程后出现故障，即刻停车与B地联系．B地收到消息后立即派货车乙从B地出发去接运甲车上的物资．货车乙遇到甲后，用了18分钟将物资从货车甲搬运到货车乙上，随后开往B地．两辆货车离开各自出发地的路程y（千米）与时间x（小时）的函数关系如图所示．（通话等其他时间忽略不计）

(1)、求货车乙在遇到货车甲前，它离开出发地的路程y关于x的函数表达式；

(2)、货车乙赶往事故地所需时间为小时；若货车乙返程速度保持与到达事故地前一致，整个过程比原计划多小时．

查看试题解析
20. 如图， $A B$ 是 $⊙ O$ 的直径，点C在 $⊙ O$ 上，点E是 $\overset{⌢}{B C}$ 的中点，延长 $A C$ 交 $B E$ 的延长线于点D，点F在 $A B$ 的延长线上， $E F ⊥ A D$ ，垂足为G．

(1)、求证： $G F$ 是 $⊙ O$ 的切线；

(2)、若 $B F = 1$ ， $E F = \sqrt{2}$ ，求 $⊙ O$ 的半径．

查看试题解析
21. 阅读材料：求 $3^{1} + 3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6}$ 的值.
解：设 $S = 3^{1} + 3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6}$ ①，
则 $3 S = 3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6} + 3^{7}$ ②.
用②-① $3 S - S = (3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6} + 3^{7}) - (3 + 3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6}) = 3^{7} - 3$
$∴ 2 S = 3^{7} - 3$ .即 $S = \frac{3^{7} - 3}{2}$ .
$∴ 3^{1} + 3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6} = \frac{3^{7} - 3}{2}$ .
以上方法我们称为“错位相减法”，请利用上述材料，解决下列问题：

(1)、（一）棋盘摆米
这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏，阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒...按这个方法放满整个棋盘就行.”国王以为要不了多少粮食，就随口答应了，结果国王输了.
国际象棋共有64个格子，则在第64格应放粒米；（用幂表示）

(2)、设国王输给阿基米德的米粒数为S，求S.

(3)、（二）拓展应用：计算： $\frac{1}{4^{3}} + \frac{1}{4^{4}} + \frac{1}{4^{5}} + ⋯ + \frac{1}{4^{n}}$ .

查看试题解析
22. 如图，抛物线 $y = a x^{2} + b x + 3$ 与x轴交于 $A (- 2 ， 0) ， B (6 ， 0)$ 两点，与y轴交于点C直线 $l ： y = \frac{1}{2} x + n$ 与抛物线交于A，D两点，与y轴交于点E．

(1)、求抛物线的解析式；

(2)、若点P是抛物线上的点且在直线l上方，连接 $P A ， P D$ ，求当 $△ P A D$ 面积最大时点P的坐标及该面积的最大值；

(3)、y轴上是否存在点Q，使 $∠ A D Q = 45 °$ ，若存在请求点Q的坐标；若不存在说明理由．

查看试题解析