山东省济宁市梁山县2022年中考数学适应性检测试卷
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列代数式的值中,一定是正数的是A、 B、 C、 D、2. 下列立体图形中,主视图是圆的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,将长方形纸片ABCD沿AE折叠,使点D恰好落在BC边上点F处.若 , ,则EC的长为( )
3. 如图,将长方形纸片ABCD沿AE折叠,使点D恰好落在BC边上点F处.若 , ,则EC的长为( ) A、2 B、 C、3 D、4. 已知是方程的两个实数根,则的值等于( )A、 B、6 C、10 D、5. 构造几何图形解决代数问题是“数形结合思想”的重要应用,小康在计算 时,构造出如图所示的图形:在Rt ACD中, , ,延长 到 , ,连接 ,得 .根据此图可求得 的结果( )
A、2 B、 C、3 D、4. 已知是方程的两个实数根,则的值等于( )A、 B、6 C、10 D、5. 构造几何图形解决代数问题是“数形结合思想”的重要应用,小康在计算 时,构造出如图所示的图形:在Rt ACD中, , ,延长 到 , ,连接 ,得 .根据此图可求得 的结果( ) A、 B、 C、 D、6. 下列不等式x≤–1的解集,表示正确的是( )A、
A、 B、 C、 D、6. 下列不等式x≤–1的解集,表示正确的是( )A、 B、
B、 C、
C、 D、
D、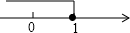 7. 已知是的外接圆,半径为 , 是的高,是 的中点,与切于 , 交的延长线于 , 则下列结论:①;②EF∥BC;③;④ . 其中正确的结论是( )
7. 已知是的外接圆,半径为 , 是的高,是 的中点,与切于 , 交的延长线于 , 则下列结论:①;②EF∥BC;③;④ . 其中正确的结论是( ) A、①②③ B、①③④ C、②③④ D、①②③④8. 如图,的内接正六边形的边心距为 , 分别以、、为圆心,正六边形的半径画弧,则图中阴影部分的面积是( )
A、①②③ B、①③④ C、②③④ D、①②③④8. 如图,的内接正六边形的边心距为 , 分别以、、为圆心,正六边形的半径画弧,则图中阴影部分的面积是( )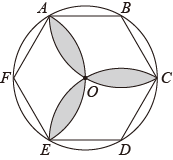 A、 B、 C、 D、9. 如图,在中,是直径,D是弦, , 垂足为 , 连接、、 , , 则下列说法中错误的是( )
A、 B、 C、 D、9. 如图,在中,是直径,D是弦, , 垂足为 , 连接、、 , , 则下列说法中错误的是( ) A、 B、 C、 D、10. 如图所示,在平行四边形中,对角线 , 相交于点 , 过点的直线分别交于点 , 于点 , , , 则平行四边形的面积( )
A、 B、 C、 D、10. 如图所示,在平行四边形中,对角线 , 相交于点 , 过点的直线分别交于点 , 于点 , , , 则平行四边形的面积( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 如图,、是半径为1的的两条切线,点、分别为切点, , 与弦交于点 , 与交于点 , 阴影部分的面积是(结果保留).
 13. 已知二次函数的图象如图所示,对称轴为直线且经过点 , 则下列结论:①;②;③;④正确结论的是填序号 .
13. 已知二次函数的图象如图所示,对称轴为直线且经过点 , 则下列结论:①;②;③;④正确结论的是填序号 . 14. 如图, 是 的平分线, 是 的平分线, 与 交于 ,若 , ,则 .
14. 如图, 是 的平分线, 是 的平分线, 与 交于 ,若 , ,则 . 15. 菱形定义:一组相等的平行四边形叫菱形.
15. 菱形定义:一组相等的平行四边形叫菱形.三、解答题
-
16. 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
 (1)、写出用含x、y的代数式表示厨房的面积是 m2;卧室的面积是
(1)、写出用含x、y的代数式表示厨房的面积是 m2;卧室的面积是m2;
(2)、写出用含x、y的代数式表示这套房的总面积是多少平方米?(3)、当x=3,y=2时,求小王这套房的总面积是多少平方米?(4)、若在(3)中,小王到某商店挑选了80cm×80cm的地砖来镶客厅和卧室,他应买多少块才够用?(结果保留整数)17. 我校团委举办了一次“中国梦·我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达到6分及以上为合格,达到9分及以上为优秀. 这次大赛中甲、乙两组学生成绩分布的条形统计图如下. (1)、补充完成下列的成绩统计分析表:
(1)、补充完成下列的成绩统计分析表:组别
平均分
中位数
方差
合格率
优秀率
甲
6.7
3.41
90%
20%
乙
7.5
1.69
80%
10%
(2)、小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏下!”观察上表,请说明小明是哪一组学生,并说明理由;(3)、如果学校准备推荐其中一个组参加县级比赛,你推荐哪一组参加?请你从两个不同的角度说明推荐理由.18. 如图在平面直角示系中,直线与轴交于点,与轴交于点 , 在第一象限内与反比例函数的图象交于点 , , 过点作轴垂足为点. (1)、点的坐标是 , 点的坐标是;(2)、求反比例函数的表达式;(3)、观察图象,在第一象限内,当时,的取值范围是 .19. 如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)、点的坐标是 , 点的坐标是;(2)、求反比例函数的表达式;(3)、观察图象,在第一象限内,当时,的取值范围是 .19. 如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF. (1)、求证:CG是⊙O的切线;(2)、若AE=2,EG=1,求由弦BC和所围成的弓形的面积.20. 某商店经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件.(1)、当销售单价为12元,每天可售出多少件?(2)、针对这种小商品的销售情况,该商店要保证每天盈利640元,同时又要使顾客得到实惠,那么销售单价应定为多少元?
(1)、求证:CG是⊙O的切线;(2)、若AE=2,EG=1,求由弦BC和所围成的弓形的面积.20. 某商店经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件.(1)、当销售单价为12元,每天可售出多少件?(2)、针对这种小商品的销售情况,该商店要保证每天盈利640元,同时又要使顾客得到实惠,那么销售单价应定为多少元?
21. 判断命题“一组对边平行另一组对边相等的四边形是平行四边形”真假,若是真命题,请给出证明;若是假命题,请修改其中一个条件使其变成真命题(一个即可)并请写出证明过程.(要求:画出图形,写出已知,求证和证明过程)22. 如图1,抛物线y=ax2过定点M( , ),与直线AB:y=kx+1相交于A、B两点. (1)、若k=﹣ ,求△ABO的面积.(2)、若k=﹣ ,在抛物线上的点P,使得△ABP的面积是△ABO面积的两倍,求P点坐标.(3)、将抛物线向右平移两个单位,再向下平移两个单位,得到抛物线C2 , 如题图2,直线y=kx﹣2(k+ )与抛物线C2的对称轴交点为G,与抛物线C2的交点为P、Q两点(点P在点Q的左侧),试探究 是否为定值,并说明理由.
(1)、若k=﹣ ,求△ABO的面积.(2)、若k=﹣ ,在抛物线上的点P,使得△ABP的面积是△ABO面积的两倍,求P点坐标.(3)、将抛物线向右平移两个单位,再向下平移两个单位,得到抛物线C2 , 如题图2,直线y=kx﹣2(k+ )与抛物线C2的对称轴交点为G,与抛物线C2的交点为P、Q两点(点P在点Q的左侧),试探究 是否为定值,并说明理由.