山东省济宁市北湖区2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、2022 B、-2022 C、 D、2. 下列计算正确的是( ).A、 B、 C、 D、3. 若二次根式有意义,则x的取值范围是( )A、 B、 C、 D、4. 下列说法正确的是( )A、为了解三名学生的视力情况,采用抽样调查 B、任意画一个三角形,其内角和是 是必然事件 C、甲、乙两名射击运动员10次射击成绩(单位:环)的平均数分别为 、 ,方差分别为 、 .若 , , ,则甲的成绩比乙的稳定 D、一个抽奖活动中,中奖概率为 ,表示抽奖20次就有1次中奖5. 如图,△ABC内接于⊙O , 若∠A=45°,OC=2,则BC的长为( )
 A、 B、 C、 D、46. 关于x的方程有增根,则m的值是( )A、0 B、2或3 C、2 D、37. 如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于AC长的一半为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别相交于点D、E,连接AE,当AB=3,AC=5时,△ABE周长为( )
A、 B、 C、 D、46. 关于x的方程有增根,则m的值是( )A、0 B、2或3 C、2 D、37. 如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于AC长的一半为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别相交于点D、E,连接AE,当AB=3,AC=5时,△ABE周长为( )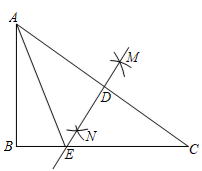 A、7 B、8 C、9 D、108. 电力公司在农村电网改造升级工程中把某一输电线铁塔建在了一个坡度为1:0.75的山坡的平台上(如图),测得 , 米,米,米,则铁塔的高度约为(参考数据: , , )( )
A、7 B、8 C、9 D、108. 电力公司在农村电网改造升级工程中把某一输电线铁塔建在了一个坡度为1:0.75的山坡的平台上(如图),测得 , 米,米,米,则铁塔的高度约为(参考数据: , , )( )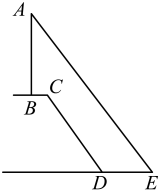 A、32.5米 B、27.5米 C、30.5米 D、58.5米9. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A、32.5米 B、27.5米 C、30.5米 D、58.5米9. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )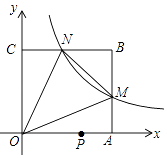 A、6 B、10 C、2 D、210. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是
A、6 B、10 C、2 D、210. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是 A、
A、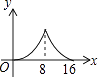 B、
B、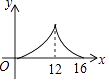 C、
C、 D、
D、
二、填空题
-
11. 分解因式: .12. 新能源汽车节能、环保,越来越受消费者喜爱.2020年某款新能源汽车销售量为15万辆,销售量逐年增加,2022年预估当年销售量为21.6万辆,求这款新能源汽车的年平均增长率是多少?可设年平均增长率为x,根据题意可列方程 .13.
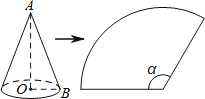
如图,圆锥的底面半径OB长为5cm,母线AB长为15cm,则这个圆锥侧面展开图的圆心角α为 度.
 14. 甲、乙两名同学观察完某个一次函数的图象,各叙述如下:
14. 甲、乙两名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点;
乙:函数的图象不经过第三象限.
根据他们的叙述,写出满足上述性质的一个函数表达式为 .
15. 如图,在平面直角坐标系中,正方形与正方形是以为位似中心的位似图形,且位似比为 , 点 , , 在x轴上,延长交射线与点 , 以为边作正方形;延长 , 交射线与点 , 以为边作正方形;…按照这样的规律继续作下去,若 , 则正方形的面积为 .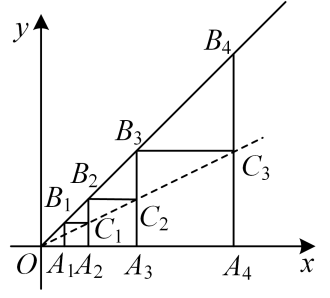
三、解答题
-
16. 已知关于x的一元二次方程 .(1)、当时,求方程的根;(2)、当时,判断方程的根的情况.17. 钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2022年新型冠状病毒防治》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据:
甲小区:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据:
成绩x(分)
甲小区
2
5
8
a
乙小区
3
7
5
5
分析数据:
统计量
平均数
中位数
众数
甲小区
85.75
87.5
b
乙小区
83.5
c
80
应用数据:
(1)、填空: , , .(2)、若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;(3)、社区管理员看完统计数据,准备从成绩在60到70分之间(包含60分和70分)的两个小区中随机抽取2人进行再测试,请求出抽取的两人恰好一个是甲小区、一个是乙小区的概率.18. 如图所示,等腰△ABC,BA=BC, AD⊥BC.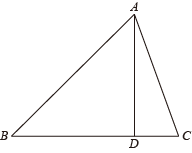 (1)、过点B作∠ABD的平分线交AD于点E(要求:保留作图痕迹,不写作法);(2)、在(1)的条件下,已知AD=BD ,求证BE=AC.19. 某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品1件共需50元;购进甲商品1件和乙商品2件共需70元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件20元出售,乙商品以每件50元出售,为满足市场需求,需购进甲、乙两种商品共60件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.20. 如图,是⊙的直径,过点A作⊙的切线,并在其上取一点C,连接交⊙于点D,的延长线交于E,连接 .
(1)、过点B作∠ABD的平分线交AD于点E(要求:保留作图痕迹,不写作法);(2)、在(1)的条件下,已知AD=BD ,求证BE=AC.19. 某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品1件共需50元;购进甲商品1件和乙商品2件共需70元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件20元出售,乙商品以每件50元出售,为满足市场需求,需购进甲、乙两种商品共60件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.20. 如图,是⊙的直径,过点A作⊙的切线,并在其上取一点C,连接交⊙于点D,的延长线交于E,连接 .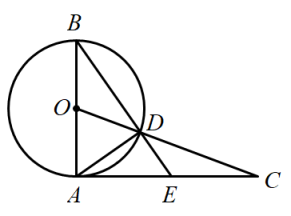 (1)、求证:;(2)、若 , , 求的长.21. 我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)、求证:;(2)、若 , , 求的长.21. 我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.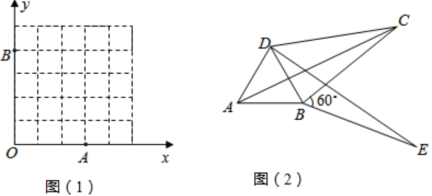 (1)、写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , .(2)、如图(1),已知格点(小正方形的顶点) , , , 请你直接写出一个以格点为顶点, , 为勾股边且对角线相等的勾股四边形的顶点M的坐标为;(3)、如图(2),将绕顶点B按顺时针方向旋转60°,得到 , 连接 , , . 求证: , 即四边形是勾股四边形;(4)、若将图(2)中绕顶点B按顺时针方向旋转a度 , 得到 , 连接 , , 则°,四边形是勾股四边形.22. 抛物线交x轴于 , 两点交y轴于点C.
(1)、写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , .(2)、如图(1),已知格点(小正方形的顶点) , , , 请你直接写出一个以格点为顶点, , 为勾股边且对角线相等的勾股四边形的顶点M的坐标为;(3)、如图(2),将绕顶点B按顺时针方向旋转60°,得到 , 连接 , , . 求证: , 即四边形是勾股四边形;(4)、若将图(2)中绕顶点B按顺时针方向旋转a度 , 得到 , 连接 , , 则°,四边形是勾股四边形.22. 抛物线交x轴于 , 两点交y轴于点C.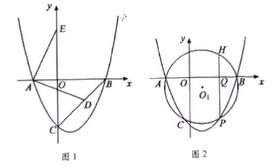 (1)、求抛物线的解析式;(2)、如图1,点D在线段上,把点D绕点A逆时针方向旋转90°,恰好落在y轴正半轴的点E处,求点E的坐标;(3)、如图2,若点P在第四象限的抛物线上,过A,B,P作⊙ , 作轴于Q,交⊙于点H,的值是否为定值?若是,请求值;若不是请说明理由.
(1)、求抛物线的解析式;(2)、如图1,点D在线段上,把点D绕点A逆时针方向旋转90°,恰好落在y轴正半轴的点E处,求点E的坐标;(3)、如图2,若点P在第四象限的抛物线上,过A,B,P作⊙ , 作轴于Q,交⊙于点H,的值是否为定值?若是,请求值;若不是请说明理由.