山东省济南市长清区2022年九年级数学第一次模拟试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
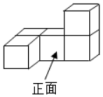
1. =( )A、-2022 B、 C、2022 D、2. 如图所示的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 据海关统计,今年第一季度我国外贸进出口总额是3710000000元人民币,数据3710000000用科学记数法表示为( )A、 B、 C、 D、4. 将直角三角尺和直尺按如图所示放置,若∠2=55°,则∠1的度数是( )
3. 据海关统计,今年第一季度我国外贸进出口总额是3710000000元人民币,数据3710000000用科学记数法表示为( )A、 B、 C、 D、4. 将直角三角尺和直尺按如图所示放置,若∠2=55°,则∠1的度数是( ) A、35° B、45° C、50° D、55°5. 以下是四个我国杰出企业代表的标志,其中是轴对称图形的是( )A、
A、35° B、45° C、50° D、55°5. 以下是四个我国杰出企业代表的标志,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. “五一”劳动节期间,某快餐店统计了5月1日至5月5日每天的用水量(单位:吨),并绘制成如图所示的折线统计图.下列结论正确的是( )
6. “五一”劳动节期间,某快餐店统计了5月1日至5月5日每天的用水量(单位:吨),并绘制成如图所示的折线统计图.下列结论正确的是( ) A、平均数是6 B、众数是7 C、中位数是5 D、极差是87. 下列运算正确的是( )A、 B、 C、 D、8. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、9. 直线经过一、二、三象限,则直线的图象可能是图中的( )A、
A、平均数是6 B、众数是7 C、中位数是5 D、极差是87. 下列运算正确的是( )A、 B、 C、 D、8. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、9. 直线经过一、二、三象限,则直线的图象可能是图中的( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在 中, , , .按以下步骤作图:①分别以点B和点C为圆心、大于 的长为半径作圆弧,两弧相交于点M和点N;②作直线MN交AC于点D , 则CD的长为( )
10. 如图,在 中, , , .按以下步骤作图:①分别以点B和点C为圆心、大于 的长为半径作圆弧,两弧相交于点M和点N;②作直线MN交AC于点D , 则CD的长为( ) A、 B、 C、 D、11. 如图,在阳光下直立于地面上的电线杆AB,落在水平面和坡面上的影子分别是BC、CD,测得米,米,斜坡CD的坡度为 , 在D处测电线杆顶端A的仰角为30°,则电线杆AB的高度为( )
A、 B、 C、 D、11. 如图,在阳光下直立于地面上的电线杆AB,落在水平面和坡面上的影子分别是BC、CD,测得米,米,斜坡CD的坡度为 , 在D处测电线杆顶端A的仰角为30°,则电线杆AB的高度为( )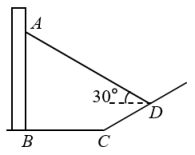 A、 B、 C、 D、12. 定义:对于二次函数y=ax2+(b+1)x+b﹣2(a≠0),若存在自变量x0 , 使得函数值等于x0成立,则称x0为该函数的不动点,对于任意实数b,该函数恒有两个相异的不动点,则实数a的取值范围为( )A、0<a<2 B、0<a≤2 C、﹣2<a<0 D、﹣2≤a<0
A、 B、 C、 D、12. 定义:对于二次函数y=ax2+(b+1)x+b﹣2(a≠0),若存在自变量x0 , 使得函数值等于x0成立,则称x0为该函数的不动点,对于任意实数b,该函数恒有两个相异的不动点,则实数a的取值范围为( )A、0<a<2 B、0<a≤2 C、﹣2<a<0 D、﹣2≤a<0二、填空题
-
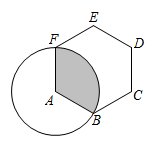
13. 分解因式:m2-6m+9= .14. 一个不透明的袋子中装有3个小球,其中2个红球,1个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率为 .15. 方程的解为 .16. 如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为 .
 17. 如图,邻边不等的矩形花园ABCD,它的一边AD利用已有的围墙(墙足够长),另外三边所围的栅栏的总长度是18m,若矩形的面积为36m2 , 则AB的长度是m.
17. 如图,邻边不等的矩形花园ABCD,它的一边AD利用已有的围墙(墙足够长),另外三边所围的栅栏的总长度是18m,若矩形的面积为36m2 , 则AB的长度是m.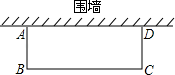 18. 如图,在正方形ABCD的对角线AC上取一点E,使得 , 连接BE并延长BE到F,使 , BF与CD相交于点H,若 , 有下列结论:①;②;③;④ . 则其中正确的结论有 .
18. 如图,在正方形ABCD的对角线AC上取一点E,使得 , 连接BE并延长BE到F,使 , BF与CD相交于点H,若 , 有下列结论:①;②;③;④ . 则其中正确的结论有 .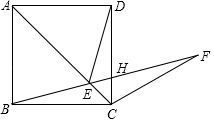
三、解答题
-
19. 计算: .20. 解不等式组并求它的整数解.21. 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.求证:AE=CF.
 22. 为庆祝中国共产党建党100周年,昆明市第十中学初中部开展了以“百年党史今天读”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成A,B,C,D,E五个等级,并绘制了如下不完整的统计图请结合统计图,解答下列问题:
22. 为庆祝中国共产党建党100周年,昆明市第十中学初中部开展了以“百年党史今天读”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成A,B,C,D,E五个等级,并绘制了如下不完整的统计图请结合统计图,解答下列问题: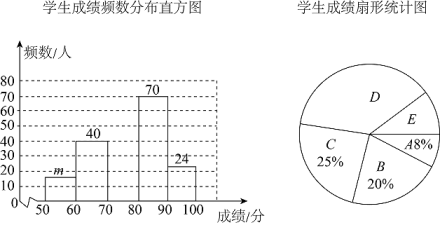
等级
成绩x
A
B
C
D
E
(1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中;(2)、补全学生成绩频数分布直方图;(3)、所抽取学生成绩的中位数落在等级;(4)、若成绩在80分及以上为优秀,学校初中部共有3000名学生,估计成绩优秀的学生有多少人?23. 如图,AB是⊙的直径, , 点P为AB延长线上一点,点C为⊙上一点,过点A作于点E,AE交⊙于点D.若点C是的中点,解答下列问题. (1)、求证:PC是⊙的切线.(2)、若 , 求AE的长.24. 企业准备购买一批爱心物资捐赠给学校.经了解,若购买洗手液300瓶和口罩200包,则共需6000元;若购买洗手液500瓶和口罩300包,则共需9500元.(1)、问:每瓶洗手液和每包口罩的价格各是多少元?(2)、现计划购买洗手液和口罩,若购买洗手液瓶数和口罩的包数之和为1000,且洗手液的瓶数不大于口罩包数的3倍.求最多购买多少瓶洗手液?25. 如图,一次函数与反比例函数的图象交于点和 .
(1)、求证:PC是⊙的切线.(2)、若 , 求AE的长.24. 企业准备购买一批爱心物资捐赠给学校.经了解,若购买洗手液300瓶和口罩200包,则共需6000元;若购买洗手液500瓶和口罩300包,则共需9500元.(1)、问:每瓶洗手液和每包口罩的价格各是多少元?(2)、现计划购买洗手液和口罩,若购买洗手液瓶数和口罩的包数之和为1000,且洗手液的瓶数不大于口罩包数的3倍.求最多购买多少瓶洗手液?25. 如图,一次函数与反比例函数的图象交于点和 . (1)、求b、k、m的值;(2)、根据图象直接写出的解集;(3)、点P是线段AB上一点,过点P作轴于点D,连接OP,若的面积为S,求S的最大值.26. 图1是边长分别为和的两个等边三角形纸片和叠放在一起(与重合)的图形.
(1)、求b、k、m的值;(2)、根据图象直接写出的解集;(3)、点P是线段AB上一点,过点P作轴于点D,连接OP,若的面积为S,求S的最大值.26. 图1是边长分别为和的两个等边三角形纸片和叠放在一起(与重合)的图形. (1)、操作:固定 , 将绕点C按顺时针方向旋转20°,连结AD,BE,如图2,则度,并直接写出线段BE与AD的数量关系 .(2)、操作:若将图1中的 , 绕点C按顺时针方向旋转120°,使点B、C、D在同一条直线上,连结AD、BE,如图3.
(1)、操作:固定 , 将绕点C按顺时针方向旋转20°,连结AD,BE,如图2,则度,并直接写出线段BE与AD的数量关系 .(2)、操作:若将图1中的 , 绕点C按顺时针方向旋转120°,使点B、C、D在同一条直线上,连结AD、BE,如图3.①线段BE与AD之间是否仍存在(1)中的结论?若是,请证明;若不是,请直接写出BE与AD之间的数量关系;
②求的度数.
(3)、若将图1中的 , 绕点C按逆时针方向旋转一个角 , 当等于多少度时,的面积最大?请直接写出答案.27. 如图,已知抛物线与x轴交于点和 , 与y轴交于点C.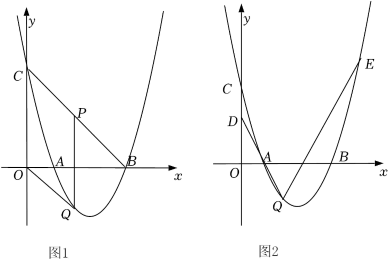 (1)、求抛物线的解析式;(2)、如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ,当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由;(3)、如图2,在(2)的条件下,D是OC的中点,过点Q的直线交抛物线于点E,且 . 在y轴上是否存在点F,使得为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ,当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由;(3)、如图2,在(2)的条件下,D是OC的中点,过点Q的直线交抛物线于点E,且 . 在y轴上是否存在点F,使得为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.