山东省济南市市中区2022年中考一模数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

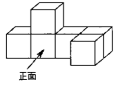
1. $- \frac{1}{2022}$ 的相反数是（）．

A、2022 B、 $- 2022$ C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 如图所示的几何体是由6个大小相同的小立方体搭成，它的主视图是（）

A、 B、 C、 D、

查看试题解析
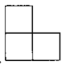3. 随着高铁的发展，预计2020年济南西客站客流量将达到2150万人，数字2150用科学记数法表示为（）

A、0.215×10⁴ B、2.15×10³ C、2.15×10⁴ D、21.5×10²

查看试题解析
4. 如图，直线 $a ∥ b ， ∠ 1 = 60 ° ， ∠ 2 = 40 °$ ，则 $∠ 3 =$ （）．

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $80 °$

查看试题解析
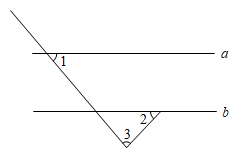5. 窗棂即窗格（窗里面的横的或竖的格）是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案，下列表示我国古代窗棂样式结构图案中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 将分别标有“中”“国”“加”“油”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀随机摸出一球，不放回；再随机摸出一球．两次摸出的球上的汉字能组成“加油”的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
7. 化简 $\frac{a^{2}}{a - 1} + \frac{a}{1 - a}$ 的结果是（）

A、a﹣1 B、a C、﹣a D、a十1

查看试题解析
8. 已知点 $A (- 2 ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (3 ， y_{3})$ 都在反比例函数 $y = \frac{3}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系正确的是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
9. △ABC在平面直角坐标系中的位置如图所示，将其绕点P顺时针旋转得到△A'B'C′，则点P的坐标是（）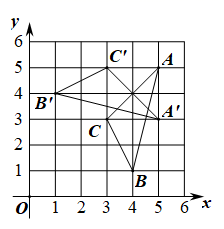

A、（4，5） B、（4，4） C、（3，5） D、（3，4）

查看试题解析
10. 如图，某同学在楼房的 $A$ 处测得荷塘的一端 $B$ 处的俯角为 $24 °$ ，荷塘另一端点D与点C，B在同一直线上，已知楼房 $A C = 32$ 米， $C D = 16$ 米；则荷塘的宽 $B D$ 为（）
( $\sin 24 ° \approx 0.41$ ， $\cos 24 ° \approx 0.91$ ， $tan 24 ° \approx 0.45$ .结果精确到0.1)

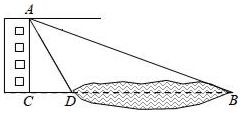A、55.1米 B、30.4米 C、51.2米 D、19.2米

查看试题解析
11. 如图，等腰三角形 $A B C$ 中， $A B = A C = 6$ ，按以下要求作图：①以点A为圆心，任意长为半径作弧，分别交 $A B ， A C$ 于D，E两点；②分别以点D、E为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧交于点F；③作射线 $A F$ ，交 $B C$ 于点M；④分别以A、B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧分别交于G，H两点；⑤作直线 $G H$ ，交 $A B$ 于点N，连接 $M N$ ．则 $M N$ 的长为（）

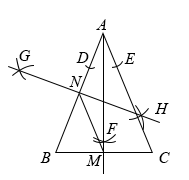A、2 B、3 C、4 D、6

查看试题解析
12. 在平面直角坐标系中，已知点A（－2，3），B（2，1），若抛物线y＝ax²－2x+1（a≠0）与线段AB有两个不同的交点，则a的取值范围是（）

A、 $- \frac{9}{16}$ ＜a≤ $- \frac{1}{2}$ 或a≥1 B、a≥ $- \frac{1}{2}$ 或a＜ $- \frac{9}{16}$ C、 $- \frac{1}{2}$ ≤a≤1且a≠0 D、a≤ $- \frac{1}{2}$ 或a≥1

查看试题解析

二、填空题

13. 因式分解 $m^{2} - 4 n^{2} =$ ．

查看试题解析
14. 转盘中6个扇形的面积相等，任意转动转盘一次，当转盘停止转动，指针落在扇形中的数为3的倍数的概率是．

查看试题解析
15. 分式方程 $\frac{3}{x + 1} = \frac{x}{x - 1} - 1$ 的解是．

查看试题解析
16. 若关于x的一元二次方程 $a x^{2} - 2 x + 1 = 0$ 有实数根，则a应满足．

查看试题解析
17. 如图，正方形 $A B C D$ 的边长为4，分别以正方形的三条边为直径在正方形内部作半圆，则阴影部分的面积是．

查看试题解析
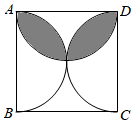18. 如图1，有一张矩形纸片 $A B C D$ ，已知 $A B = 10$ ， $A D = 12$ ，现将纸片进行如下操作：先将纸片沿折痕 $B F$ 进行折叠，使点A落在 $B C$ 边上的点E处，点F在 $A D$ 上（如图2）；然后将纸片沿折痕 $D H$ 进行第二次折叠，使点C落在第一次的折痕 $B F$ 上的点G处，点H在 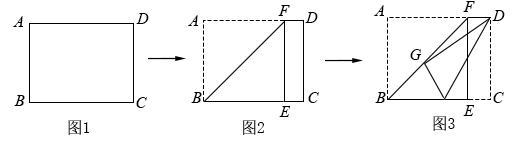$B C$ 上（如图3），则 $G H$ 的长是．

查看试题解析

三、解答题

19. 计算： ${(\frac{1}{3})}^{- 1} - {(\sqrt{5} - 2)}^{0} + \sqrt{12} - \tan 60^{°}$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} x - 3 < \frac{x - 3}{2} \\ 3 (x - 1) - 1 \geq x - 8 \end{array}$ ，并写出其整数解．

查看试题解析
21. 如图，在 $▱ A B C D$ 中，点E在 $A B$ 的延长线上，点F在 $C D$ 的延长线上，满足 $B E = D F$ .连接 $E F$ ，分别与 $B C$ ， $A D$ 交于点 $G$ ，H.求证： $E G = F H$ .

查看试题解析
22. 为倡导绿色健康节约的生活方式，某社区开展“减少方便筷使用，共建节约型社区”活动．志愿者随机抽取了社区内50名居民，对其5月份方便筷使用数量进行了调查，并对数据进行了统计整理，以下是部分数据和不完整的统计图表：
方便筷使用数量在 $5 \leq x < 15$ 范围内的数据：
5，7，12，9，10，12，8，8，10，11，6，9，13，6，12，8，7．
不完整的统计图表：
方便筷使用数量统计表
组别
使用数量（双）
频数
A
$0 ≤ x < 5$
14
B
$5 \leq x < 10$
C
$10 \leq x < 15$
D
$15 \leq x < 20$
$a$
E
$x ≥ 20$
10
合
50
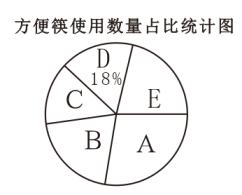
请结合以上信息回答下列问题：

(1)、统计表中的 $a =$ ；

(2)、统计图中 $E$ 组对应扇形的圆心角为度；

(3)、 $C$ 组数据的众数是；调查的50名居民5月份使用方便筷数量的中位数是；

(4)、根据调查结果，请你估计该社区2000名居民5月份使用方便筷数量不少于15双的人数．

查看试题解析
23. 已知：如图， $A B$ 是 $⊙ O$ 的直径C，D是 $⊙ O$ 上两点，过点C的切线交 $D A$ 的延长线于点E， $D E ⊥ C E$ ，连接 $C D ， B C$ ．

(1)、求证： $∠ D A B = 2 ∠ A B C$ ；

(2)、若 $t a n ∠ A D C = \frac{1}{2} ， B C = 8$ ，求 $⊙ O$ 的半径．

查看试题解析
24. 某商场销售10台A型和20台B型加湿器的利润为2500元，销售20台A型和10台B型加湿器的利润为2000元.

(1)、求每台A型加湿器和每台B型加湿器的销售利润；

(2)、该商场计划一次购进两种型号的加湿器共100台，设购进A型加湿器 $x$ 台，这100台加湿器的销售总利润为y元.
①求y关于x的函数关系式；

②若B型加湿器的进货量不超过A型加湿器的2倍，则该商场应怎样进货才能使销售总利润最大？

查看试题解析
25. 如图，一次函数y=﹣x+3的图象与反比例函数y= $\frac{k}{x}$ （k≠0）在第一象限的图象交于A（1，a）和B两点，与x轴交于点C．

(1)、求反比例函数的解析式；

(2)、若点P在x轴上，且△APC的面积为5，求点P的坐标；

(3)、若点P在y轴上，是否存在点P，使△ABP是以AB为一直角边的直角三角形？若存在，求出所有符合条件的P点坐标；若不存在，请说明理由．

查看试题解析
26. 在 $R t △ A B C$ 中与 $R t △ D C E$ 中， $∠ A C B = ∠ D C E = 90 ° ， ∠ B A C = ∠ D E C = 30 °$ ， $A C = D C = \sqrt{3}$ ，将 $R t △ D C E$ 绕点 $C$ 顺时针旋转，连接 $B D ， A E$ ，点 $F ， G$ 分别是 $B D ， A E$ 的中点，连接 $C F ， C G$ ．

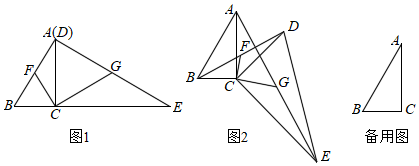(1)、观察猜想
如图1，当点 $D$ 与点 $A$ 重合时， $C F$ 与 $C G$ 的数量关系是，位置关系是；

(2)、类比探究
当点 $D$ 与点 $A$ 不重合时，（1）中的结论是否成立？如果成立，请仅就图2的情形给出证明；如果不成立，请说明理由．

(3)、问题解决在 $R t △ D C E$ 旋转过程中，请直接写出 $△ C F G$ 的面积的最大值与最小值．

查看试题解析
27. 如图，抛物线 $M ： y = \frac{1}{2} x^{2} + b x + c$ 交y轴于点 $A (0 ， - 1)$ ，且过点 $P (- 1 ， - \frac{5}{2})$ 点B是抛物线M上一个动点，过B作 $B C ∥ O A$ ，以B为圆心，2为半径的圆交直线 $B C$ 于D、E两点（点E位于点D下方）

(1)、求抛物线M的解析式；

(2)、连接 $A B$ 交 $⊙ B$ 于点F，连接 $E F ， A D$ ．若 $△ A B D$ 是以 $B D$ 为直角边的直角三角形，求 $∠ B E F$ 的度数；

(3)、取 $A D$ 的中点Q，连接 $P Q$ ，求线段 $P Q$ 的最小值．（直接写出答案）

查看试题解析

组别	使用数量（双）	频数
A	$0 ≤ x < 5$	14
B	$5 \leq x < 10$
C	$10 \leq x < 15$
D	$15 \leq x < 20$	$a$
E	$x ≥ 20$	10
合		50