山东省济南市槐荫区2022年九年级一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 下列各数是无理数的是( )A、0 B、 C、 D、3.142. 如图所示,该几何体的左视图是( )
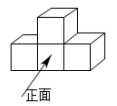 A、
A、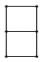 B、
B、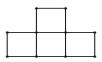 C、
C、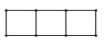 D、
D、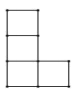 3. 2021年槐荫教育大会发布了“教育提升三年行动计划”,计划中明确提出:3年内提供中小学学位20160个、公办幼儿园学位9180个.其中20160用科学记数法表示为( )A、 B、 C、 D、4. 下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )A、
3. 2021年槐荫教育大会发布了“教育提升三年行动计划”,计划中明确提出:3年内提供中小学学位20160个、公办幼儿园学位9180个.其中20160用科学记数法表示为( )A、 B、 C、 D、4. 下列各图中,已知∠1=∠2,不能证明AB∥CD的是( )A、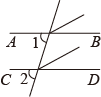 B、
B、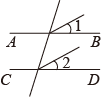 C、
C、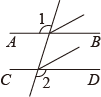 D、
D、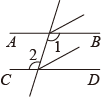 5. 下列运算正确的是( )A、 B、 C、 D、6. 化简的结果是( )A、 B、 C、 D、7. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 化简的结果是( )A、 B、 C、 D、7. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为( )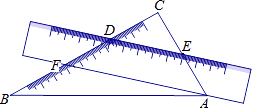 A、10° B、15° C、20° D、25°8. 若 , 则一次函数的图象是( )A、
A、10° B、15° C、20° D、25°8. 若 , 则一次函数的图象是( )A、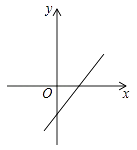 B、
B、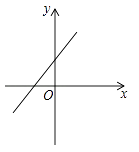 C、
C、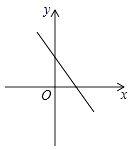 D、
D、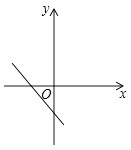 9. 如图,以直角坐标系的原点O为圆心,以1为半径作圆.若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为 , 则点P的坐标为( )
9. 如图,以直角坐标系的原点O为圆心,以1为半径作圆.若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为 , 则点P的坐标为( )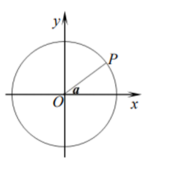 A、 B、 C、 D、10. 如图, 是 的直径,点A,C在 上, , 交 于点G.若 .则 的度数为( )
A、 B、 C、 D、10. 如图, 是 的直径,点A,C在 上, , 交 于点G.若 .则 的度数为( )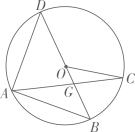 A、 B、 C、 D、11. 如图,菱形ABCD中对角线AC与BD相交于点F,且 , , 若点P是对角线BD上一动点,连接AP,将AP绕点A逆时针旋转使得 , 连接PE,取AD的中点O,连接OE,则在点P的运动过程中,线段OE的最小值为( )
A、 B、 C、 D、11. 如图,菱形ABCD中对角线AC与BD相交于点F,且 , , 若点P是对角线BD上一动点,连接AP,将AP绕点A逆时针旋转使得 , 连接PE,取AD的中点O,连接OE,则在点P的运动过程中,线段OE的最小值为( )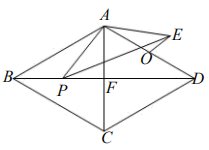 A、2 B、4 C、 D、12. 二次函数y=ax2+2ax+3(a为常数,a≠0),当a-1≤x≤2时二次函数的函数值y恒小于4,则a的取值范围为( )A、 B、 C、或 D、或
A、2 B、4 C、 D、12. 二次函数y=ax2+2ax+3(a为常数,a≠0),当a-1≤x≤2时二次函数的函数值y恒小于4,则a的取值范围为( )A、 B、 C、或 D、或二、填空题
-
13. 分解因式 .14. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是.
 15. 为落实“双减”政策,学校随机调查了30名学生一周平均每天的睡眠时间,统计结果如下表,则这些被调查学生睡眠时间的中位数是小时.
15. 为落实“双减”政策,学校随机调查了30名学生一周平均每天的睡眠时间,统计结果如下表,则这些被调查学生睡眠时间的中位数是小时.时间/小时
7
8
9
10
人数
6
11
9
4
16. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为660平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为 .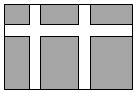 17. 矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=.
17. 矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=.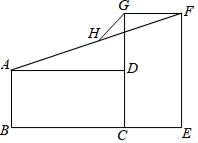 18. 如图,线段 , 在线段AB上有一点C,当时,以BC为直角边在AB上方作等腰 , , P为平面内一点,连接PB,PC,将和分别沿DB,PC翻折得到和 , 若A、、P恰好共线,则线段PD的最小值是 .
18. 如图,线段 , 在线段AB上有一点C,当时,以BC为直角边在AB上方作等腰 , , P为平面内一点,连接PB,PC,将和分别沿DB,PC翻折得到和 , 若A、、P恰好共线,则线段PD的最小值是 .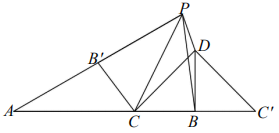
三、解答题
-
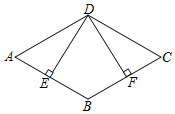
19.20. 解不等式组.21. 如图,在菱形ABCD中,过点D分别作DE⊥AB于点E,作DF⊥BC于点F.求证:AE=CF.
 22. 2021年12月16日槐荫区2021“勾股数学”杯计算大赛在全区七年级学生中拉开序幕,为准备此次大赛,某校组织了模拟比赛,并随机抽取了部分学生的成绩进行统计,按成绩分成A,B,C,D,E五个等级,绘制了如下统计图,请结合统计图,回答下列问题:
22. 2021年12月16日槐荫区2021“勾股数学”杯计算大赛在全区七年级学生中拉开序幕,为准备此次大赛,某校组织了模拟比赛,并随机抽取了部分学生的成绩进行统计,按成绩分成A,B,C,D,E五个等级,绘制了如下统计图,请结合统计图,回答下列问题:等级
成绩x
A
B
C
D
E
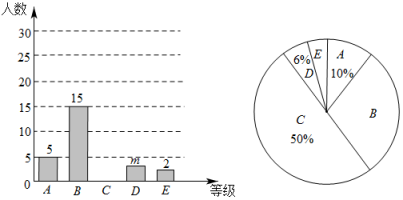 (1)、本次调查一共随机抽取了名学生的成绩,条形统计图中m=;(2)、补全条形统计图;(3)、扇形统计图中B等级所占的圆心角为度;(4)、该学校七年级共500名学生,估计成绩在110分以上的有多少人?23. 如图,以BC为直径的⊙O交△ABC的边AB于点D,过点D作⊙O的切线交AC于点E,且AC=BC.
(1)、本次调查一共随机抽取了名学生的成绩,条形统计图中m=;(2)、补全条形统计图;(3)、扇形统计图中B等级所占的圆心角为度;(4)、该学校七年级共500名学生,估计成绩在110分以上的有多少人?23. 如图,以BC为直径的⊙O交△ABC的边AB于点D,过点D作⊙O的切线交AC于点E,且AC=BC.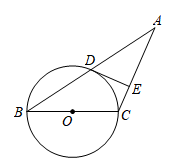 (1)、求证:DE⊥AC;(2)、若BC=4cm,AD=3cm,求AE的长.24. 2021年11月,某网店当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为32000元,12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为52000元.(1)、求“冰墩墩”和“雪容融”的销售单价;(2)、已知“冰墩墩”和“雪容融”的成本分别为102元/个和60元/个.由于冬奥会的举行,这两款毛绒玩具持续热销,于是该店再次购进这两款毛绒玩具共600个,其中“雪容融”的数量不超过“冰墩墩”数量的2倍,若购进的这两款毛绒玩具全部售出,则“冰墩墩”购进多少个时该店当月销售利润最大,并求出最大利润.25. 如图1,一次函数y=kx-3(k≠0)的图象与y轴交于点B,与反比例函数y=(x>0)的图象交于点A(8,1).
(1)、求证:DE⊥AC;(2)、若BC=4cm,AD=3cm,求AE的长.24. 2021年11月,某网店当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为32000元,12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为52000元.(1)、求“冰墩墩”和“雪容融”的销售单价;(2)、已知“冰墩墩”和“雪容融”的成本分别为102元/个和60元/个.由于冬奥会的举行,这两款毛绒玩具持续热销,于是该店再次购进这两款毛绒玩具共600个,其中“雪容融”的数量不超过“冰墩墩”数量的2倍,若购进的这两款毛绒玩具全部售出,则“冰墩墩”购进多少个时该店当月销售利润最大,并求出最大利润.25. 如图1,一次函数y=kx-3(k≠0)的图象与y轴交于点B,与反比例函数y=(x>0)的图象交于点A(8,1).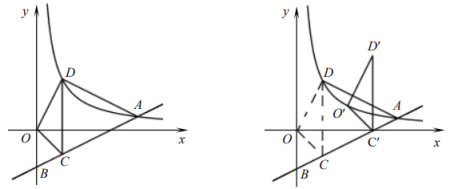 (1)、求出一次函数与反比例函数的解析式;(2)、点C是线段AB上一点(不与A,B重合),过点C作y轴的平行线与该反比例函数的图象交于点D,连接OC,OD,AD,当tan∠ADC=2时,求点C的坐标;(3)、在(2)的前提下,将△OCD沿射线BA方向平移一定的距离后,得到△O'CD',若点O的对应点O'恰好落在该反比例函数图象上(如图2),求出点O',D'的坐标.26. 如图1,正方形ABCD与正方形AEGF有公共顶点A,点B,D分别在边AE和AF上,连接BF,DE,M是DE的中点,连接AM交BF于点N.
(1)、求出一次函数与反比例函数的解析式;(2)、点C是线段AB上一点(不与A,B重合),过点C作y轴的平行线与该反比例函数的图象交于点D,连接OC,OD,AD,当tan∠ADC=2时,求点C的坐标;(3)、在(2)的前提下,将△OCD沿射线BA方向平移一定的距离后,得到△O'CD',若点O的对应点O'恰好落在该反比例函数图象上(如图2),求出点O',D'的坐标.26. 如图1,正方形ABCD与正方形AEGF有公共顶点A,点B,D分别在边AE和AF上,连接BF,DE,M是DE的中点,连接AM交BF于点N.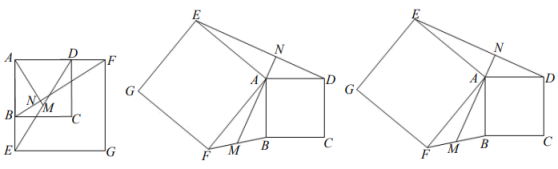 (1)、【观察猜想】
(1)、【观察猜想】线段BF与AM之间的数量关系是 , 位置关系是;
(2)、【问题呈现】将图1中的正方形AEGF绕点A顺时针旋转至图2的位置,AM所在直线交DE于点N,其他条件不变,请尝试探究线段DE与AM之间的关系是否仍然成立?
【探究思路】
延长AM至点H,使 , 连接BH,可证明 , 从而将线段DE转化为线段AH,进而探究所需结论.
【问题解决】
①请在图2中按要求作出辅助线,并写出的证明过程;
②线段DE与AM之间的关系是否仍然成立?并说明理由.
(3)、若 , 将图1中的正方形AEGF绕点A旋转一周,BN是否存在最小值?若存在请求出最小值,若不存在请说明理由.27. 如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C,D为线段AB上一点.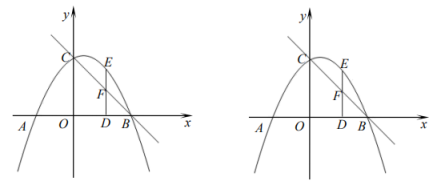 (1)、求A,B,C三点的坐标;(2)、过点D作x轴的垂线与抛物线交于点E,与直线BC相交于点F,求出点E到直线BC距离d的最大值;(3)、连接CD,作点B关于CD的对称点 , 连接 , . 在点D的运动过程中,能否等于45°?若能,请直接写出此时点的坐标,若不存在请说明理由.
(1)、求A,B,C三点的坐标;(2)、过点D作x轴的垂线与抛物线交于点E,与直线BC相交于点F,求出点E到直线BC距离d的最大值;(3)、连接CD,作点B关于CD的对称点 , 连接 , . 在点D的运动过程中,能否等于45°?若能,请直接写出此时点的坐标,若不存在请说明理由.