山东省济南市高新区2022年中考数学二模试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. ﹣2022的绝对值是( )A、2022 B、 C、﹣2022 D、2. 三个大小一样的正方体按如图摆放,它的主视图是( )
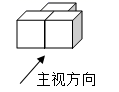 A、
A、 B、
B、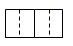 C、
C、 D、
D、 3. 今年有超过 110 000名志愿者为北京冬奥会奉献了热情服务.将 110 000用科学记数法表示应为( )A、11×104 B、1.1×105 C、1.1×106 D、0.11×1064. 如图,将三角板的直角顶点放在两条平行线中的直线AB上,若∠1=22°,则∠2的度数为( )
3. 今年有超过 110 000名志愿者为北京冬奥会奉献了热情服务.将 110 000用科学记数法表示应为( )A、11×104 B、1.1×105 C、1.1×106 D、0.11×1064. 如图,将三角板的直角顶点放在两条平行线中的直线AB上,若∠1=22°,则∠2的度数为( ) A、78° B、68° C、22° D、60°5. 第24届冬季奥林匹克运动会于2022年2月4日至2月20日在中国北京市和张家口市联合举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )A、
A、78° B、68° C、22° D、60°5. 第24届冬季奥林匹克运动会于2022年2月4日至2月20日在中国北京市和张家口市联合举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列计算正确的是( )A、a4•a=a4 B、(a2)3=a6 C、a2+a3=a5 D、a•a=2a7. 在一个不透明的口袋中,放置6个红球,2个白球和n个黄球.这些小球除颜色外其余均相同,数学小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值可能是( )
6. 下列计算正确的是( )A、a4•a=a4 B、(a2)3=a6 C、a2+a3=a5 D、a•a=2a7. 在一个不透明的口袋中,放置6个红球,2个白球和n个黄球.这些小球除颜色外其余均相同,数学小组每次摸出一个球记录下颜色后再放回,并且统计了黄球出现的频率,如图,则n的值可能是( ) A、12 B、10 C、8 D、168. 如图,将“笑脸”图标向右平移3个单位长度,再向下平移1个单位长度,则点P的对应点坐标是( )
A、12 B、10 C、8 D、168. 如图,将“笑脸”图标向右平移3个单位长度,再向下平移1个单位长度,则点P的对应点坐标是( ) A、 B、 C、 D、9. 下列图象能表示一次函数的是( )A、
A、 B、 C、 D、9. 下列图象能表示一次函数的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图所示,矩形ABCD中AB=3,BC=4,连接AC,按下列方法作图:以点C为圆心,适当长为半径画弧,分别交CA、CD于点E、F;分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线CG交AD于点H,则DH的长度为( )
10. 如图所示,矩形ABCD中AB=3,BC=4,连接AC,按下列方法作图:以点C为圆心,适当长为半径画弧,分别交CA、CD于点E、F;分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线CG交AD于点H,则DH的长度为( ) A、 B、 C、1 D、11. 为出行方便,近日来越来越多的长春市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,车轮半径为30 cm,当BC=60 cm时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为( )(结果精确到1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈1.41)
A、 B、 C、1 D、11. 为出行方便,近日来越来越多的长春市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,车轮半径为30 cm,当BC=60 cm时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为( )(结果精确到1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈1.41) A、90cm B、86cm C、82cm D、80cm12. 已知抛物线y=ax2+bx+c(a、b、c是常数,a<0)经过点(﹣2,0),其对称轴为直线x=1,有下列结论:①c>0;②9a+3b+c>0;
A、90cm B、86cm C、82cm D、80cm12. 已知抛物线y=ax2+bx+c(a、b、c是常数,a<0)经过点(﹣2,0),其对称轴为直线x=1,有下列结论:①c>0;②9a+3b+c>0;③若方程ax2+bx+c+1=0有解x1、x2 , 满足x1<x2 , 则x1<﹣2,x2>4;
④抛物线与直线y=x交于P、Q两点,若PQ , 则a=﹣1;
其中,正确结论的个数是( )个.
A、4 B、3 C、2 D、1二、填空题
-
13. 分解因式:n2﹣100= .14. 小红在地上画正方形ABCD,并顺次连接各边中点,得到如图所示的图形,然后在一定距离外向正方形内掷小石子,若每一次都掷在正方形ABCD内,且机会均等,则掷中阴影部分的概率是 .
 15. 如图,边长为2的正方形ABCD的对角线AC、BD相交于点O,若以C为圆心,CO的长为半径画圆,则图中阴影部分的面积是 .
15. 如图,边长为2的正方形ABCD的对角线AC、BD相交于点O,若以C为圆心,CO的长为半径画圆,则图中阴影部分的面积是 .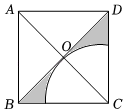 16. 已知方程组 和方程组 有相同的解,则m的值是 .17. 如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是.
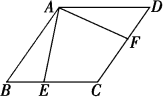
16. 已知方程组 和方程组 有相同的解,则m的值是 .17. 如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是. 18. 如图,矩形ABCD中,E为CD上一点,F为AB上一点,分别沿AE,CF折叠,D,B两点刚好都落在矩形内一点P,且∠APC=120°,则AB:AD= .
18. 如图,矩形ABCD中,E为CD上一点,F为AB上一点,分别沿AE,CF折叠,D,B两点刚好都落在矩形内一点P,且∠APC=120°,则AB:AD= .
三、解答题
-
19. 计算: .20. 求不等式组的所有整数解.21. 如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
 22. 某校举行了“风雨百年路,青春心向党”知识竞赛,现从七、八年级中各随机抽取20名学生的测试成绩(满分10分,8分及以上为优秀)进行整理和分析如下:
22. 某校举行了“风雨百年路,青春心向党”知识竞赛,现从七、八年级中各随机抽取20名学生的测试成绩(满分10分,8分及以上为优秀)进行整理和分析如下:七年级20名学生的测试成绩为:
7,8,7,8,7,5,5,9,10,9,7,5,8,7,7,7,9,8,10,7
八年级20名学生的测试成绩如下:

两个年级分析数据如表:
年级
平均数
众数
中位数
6分以上人数百分比
七年级
7.5
7
b
c
八年级
7.5
a
7.5
90%
根据以上信息,解答下列问题:
(1)、a= , b= , c=;(2)、如果八年级参加测试有500名学生,估计成绩为优秀的学生人数有多少人?(3)、根据以上数据,你认为七、八年级中哪个年级学生测试成绩较好?请说理由.23. 如图,AB是半圆O的直径,半径OC⊥AB,D是OC延长线上任意一点,DE切半圆O于点E,连结AE,交OC于点F. (1)、求证:DE=DF.(2)、若CD=2,tan∠AFO=3,求EF的长.24. 为支援贫困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.(1)、求A,B两种学习用品的单价各是多少元;(2)、若购买A、B两种学习用品共100件,且总费用不超过2800元,则最多购买B型学习用品多少件?25. 已知反比例函数y图象过第二象限内的点A(﹣2,2),若直线y=ax+b经过点A,并且经过反比例函数y的图象上另一点B(m,﹣1),与x轴交于点M.
(1)、求证:DE=DF.(2)、若CD=2,tan∠AFO=3,求EF的长.24. 为支援贫困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.(1)、求A,B两种学习用品的单价各是多少元;(2)、若购买A、B两种学习用品共100件,且总费用不超过2800元,则最多购买B型学习用品多少件?25. 已知反比例函数y图象过第二象限内的点A(﹣2,2),若直线y=ax+b经过点A,并且经过反比例函数y的图象上另一点B(m,﹣1),与x轴交于点M. (1)、求反比例函数的解析式和直线y=ax+b解析式.(2)、若点C的坐标是(0,﹣2),求△CAB的面积.(3)、在x轴上是否存在一点P,使△PAO为等腰三角形?若存在,请求出P点坐标;若不存在,请说明理由.26. 如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点F,G,H分别是BE,CD,BC的中点.
(1)、求反比例函数的解析式和直线y=ax+b解析式.(2)、若点C的坐标是(0,﹣2),求△CAB的面积.(3)、在x轴上是否存在一点P,使△PAO为等腰三角形?若存在,请求出P点坐标;若不存在,请说明理由.26. 如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点F,G,H分别是BE,CD,BC的中点. (1)、观察猜想:图1中,△FGH的形状是 ;(2)、探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△FGH的形状是否发生改变?并说明理由;(3)、拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=3,AB=7,请直接写出△FGH的周长的最大值.27. 已知:抛物线经过A(-1,0),B(3,0),C(0,3)三点.
(1)、观察猜想:图1中,△FGH的形状是 ;(2)、探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△FGH的形状是否发生改变?并说明理由;(3)、拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=3,AB=7,请直接写出△FGH的周长的最大值.27. 已知:抛物线经过A(-1,0),B(3,0),C(0,3)三点. (1)、求抛物线的解析式;(2)、如图1,点P为直线BC上方抛物线上任意一点,连PC、PB、PO,PO交直线BC于点E,设 , 求当k取最大值时点P的坐标,并求此时k的值.(3)、如图2,点Q为抛物线对称轴与x轴的交点,点C关于x轴的对称点为点D.
(1)、求抛物线的解析式;(2)、如图1,点P为直线BC上方抛物线上任意一点,连PC、PB、PO,PO交直线BC于点E,设 , 求当k取最大值时点P的坐标,并求此时k的值.(3)、如图2,点Q为抛物线对称轴与x轴的交点,点C关于x轴的对称点为点D.①求△BDQ的周长及tan∠BDQ的值;
②点M是y轴负半轴上的点,且满足(t为大于0的常数),求点M的坐标.