山东省东营市2022年中考二模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. -3的倒数是( )A、 B、 C、 D、32. 下列运算中,正确的是( )A、 B、 C、 D、3. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、
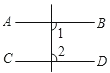 B、
B、 C、
C、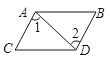 D、
D、 4. 如果点P(m,1﹣2m)在第一象限,那么m的取值范围是 ( )A、 B、 C、 D、5. 某中学篮球队12名队员的年龄情况如下表:
4. 如果点P(m,1﹣2m)在第一象限,那么m的取值范围是 ( )A、 B、 C、 D、5. 某中学篮球队12名队员的年龄情况如下表:年龄/岁
12
13
14
15
16
人数
1
3
4
2
2
关于这12名队员的年龄,下列说法中正确的是( )
A、众数为14 B、极差为3 C、中位数为13 D、平均数为146. 根据如图提供的信息,小红去商店买一只水瓶和一只杯子应付( ) A、30元 B、32元 C、31元 D、34元7. 如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A、30元 B、32元 C、31元 D、34元7. 如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( ) A、∠ABD=∠BDC,OA=OC B、∠ABC=∠ADC,AD∥BC C、∠ABC=∠ADC,AB=CD D、∠ABD=∠BDC,∠BAD=∠DCB8. 如图一个圆柱,底圆周长10cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬行( )cm .
A、∠ABD=∠BDC,OA=OC B、∠ABC=∠ADC,AD∥BC C、∠ABC=∠ADC,AB=CD D、∠ABD=∠BDC,∠BAD=∠DCB8. 如图一个圆柱,底圆周长10cm,高4cm,一只蚂蚁沿外壁爬行,要从A点爬到B点,则最少要爬行( )cm . A、9 B、14 C、 D、9. 如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
A、9 B、14 C、 D、9. 如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )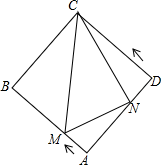 A、
A、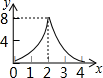 B、
B、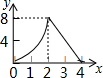 C、
C、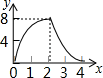 D、
D、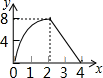 10. 如图,在正方形ABCD中,以BC为边作等边 , 延长BP,CP分别交AD于点E,F,连接BD,DP,BD与CF相较于点H,给出下列结论:;;∽; , 其中正确的是
10. 如图,在正方形ABCD中,以BC为边作等边 , 延长BP,CP分别交AD于点E,F,连接BD,DP,BD与CF相较于点H,给出下列结论:;;∽; , 其中正确的是 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 新冠肺炎患者喷嚏、咳嗽、说话的飞沫,直接吸入都会导致感染,所以我们要戴口罩,医用口罩可以过滤小至0.000004米颗粒,用科学记数法表示0.000004是 .12. 分解因式: .13. 有5张背面完全相同的卡片,每张正面分别有正三角形、平行四边形、菱形、正方形和圆,现将其全部正面朝下搅匀,从中任取一张卡片,抽中正面画的图形是中心对称图形的概率为 .14. 如图,已知A(4,0),B(3,3),以OA、AB为边作▱OABC,则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为 .
 15. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=10,则△ABD的面积是;
15. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=10,则△ABD的面积是; 16. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积是 .
16. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积是 .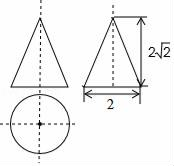 17. 如图,在平面直角坐标系中,若A(0,3),B(-2,1),在x轴上存在点P,使P到A,B两点的距离之和最小,则点P的坐标为 .
17. 如图,在平面直角坐标系中,若A(0,3),B(-2,1),在x轴上存在点P,使P到A,B两点的距离之和最小,则点P的坐标为 . 18. 已知正方形 , , …按如图所示放置,点 , , …在直线上, , , …在x轴上,则的坐标是 .
18. 已知正方形 , , …按如图所示放置,点 , , …在直线上, , , …在x轴上,则的坐标是 .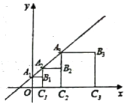
三、解答题
-
19.(1)、计算:;(2)、先化简,再求值:
, 并从 , , 2中选一个合适的数作为a的值代入求值.
20. 《中国汉字听写大会》唤醒了很多人对文字基本功的重视和对汉字文化的学习,我市某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:抽取的200名学生海选成绩分组表
组别
海选成绩x
A组
50≤x<60
B组
60≤x<70
C组
70≤x<80
D组
80≤x<90
E组
90≤x≤100
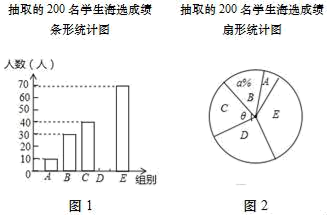
请根据所给信息,解答下列问题:
(1)、请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(2)、在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 , 表示C组扇形的圆心角θ的度数为度;(3)、规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?(4)、经过统计发现,在E组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?21. 为了防止水土流失,某村开展绿化荒山活动,计划经过若干年使本村绿化总面积新增360万平方米.自2014年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.问实际每年绿化面积多少万平方米?22. 如图,已知点P是⊙O外一点,直线PA与⊙O相切于点B,直线PO分别交⊙O于点C、D,∠PAO=∠PDB,OA交BD于点E. (1)、求证:OA∥BC;(2)、当⊙O的半径为10,BC=8时,求AE的长.23. 已知反比例函数(k≠0)的图像与一次函数的图像交于点A(-6,2),B(2,-6),且一次函数图像与x轴交于点C.
(1)、求证:OA∥BC;(2)、当⊙O的半径为10,BC=8时,求AE的长.23. 已知反比例函数(k≠0)的图像与一次函数的图像交于点A(-6,2),B(2,-6),且一次函数图像与x轴交于点C. (1)、求反比例函数与一次函数表达式;(2)、求△AOB的面积.24. 如图1,在 中, ,点D,E分别在边 上,且 ,连接 .现将 绕点A顺时针方向旋转,旋转角为 ,如图2,连接 .
(1)、求反比例函数与一次函数表达式;(2)、求△AOB的面积.24. 如图1,在 中, ,点D,E分别在边 上,且 ,连接 .现将 绕点A顺时针方向旋转,旋转角为 ,如图2,连接 .
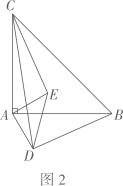
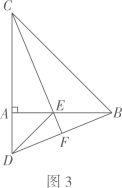 (1)、当 时,求证: ;(2)、如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;(3)、在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.25. 已知抛物线的对称轴是 , 且与x轴交于A、两点,与y轴交于C点.
(1)、当 时,求证: ;(2)、如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;(3)、在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.25. 已知抛物线的对称轴是 , 且与x轴交于A、两点,与y轴交于C点. (1)、求抛物线的解析式;(2)、如图1,设点D是线段BC上的一动点,过D作x轴的垂线,交抛物线于E,当线段DE的长度最大时,判断此时四边形OCDE的形状并说明理由;(3)、如图2,设P是抛物线上且位于直线BC上方的点,求△BCP面积的最大值.
(1)、求抛物线的解析式;(2)、如图1,设点D是线段BC上的一动点,过D作x轴的垂线,交抛物线于E,当线段DE的长度最大时,判断此时四边形OCDE的形状并说明理由;(3)、如图2,设P是抛物线上且位于直线BC上方的点,求△BCP面积的最大值.