山东省滨州市惠民县2022年中考一模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. 在0, , , 2中,最小的数是( )A、0 B、 C、2 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图,直线 , 等腰直角的两个顶点A、B分别落在直线、上,垂足为点C,若 , 则的度数是( )
 A、35° B、30° C、45° D、60°4. 如图所示,是由五个相同的小正方体搭成的几何体,其左视图是( )
A、35° B、30° C、45° D、60°4. 如图所示,是由五个相同的小正方体搭成的几何体,其左视图是( ) A、
A、 B、
B、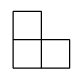 C、
C、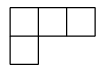 D、
D、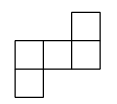 5. 在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法错误的是( )A、众数是5 B、中位数是5 C、平均数是6 D、方差是3.66. 等式 成立的x的取值范围在数轴上可表示为( )A、
5. 在一次数学答题比赛中,五位同学答对题目的个数分别为7,5,3,5,10,则关于这组数据的说法错误的是( )A、众数是5 B、中位数是5 C、平均数是6 D、方差是3.66. 等式 成立的x的取值范围在数轴上可表示为( )A、 B、
B、 C、
C、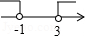 D、
D、 7. 关于x的一元二次方程有两个相等的实数根,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 有四张反面无差别的卡片,其正面分别印有国际数学家大会的会标,现将四张卡片正面朝下放置,混合均匀后从中随机抽取两张,则抽到的卡片正面图案都是中心对称图形的概率为( )
7. 关于x的一元二次方程有两个相等的实数根,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 有四张反面无差别的卡片,其正面分别印有国际数学家大会的会标,现将四张卡片正面朝下放置,混合均匀后从中随机抽取两张,则抽到的卡片正面图案都是中心对称图形的概率为( ) A、 B、 C、 D、9. 如图,点C在反比例函数的图象上,过点C的直线与x轴、y轴分别交于点A、B,且 , 的面积为1,则k的值为( )
A、 B、 C、 D、9. 如图,点C在反比例函数的图象上,过点C的直线与x轴、y轴分别交于点A、B,且 , 的面积为1,则k的值为( )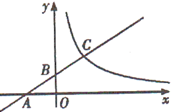 A、 B、2 C、3 D、410. 如图,是的外接圆,AD是的直径,的半径为 , , 则的值是( )
A、 B、2 C、3 D、410. 如图,是的外接圆,AD是的直径,的半径为 , , 则的值是( ) A、 B、 C、 D、11. 已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤方程的两个根的和为2,其中正确的有( )
A、 B、 C、 D、11. 已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤方程的两个根的和为2,其中正确的有( ) A、2个 B、3个 C、4个 D、5个12. 如图,将边长为9的正方形ABCD沿MN折叠,使点B落在CD边上的处,点A对应点为 , 且 , 则AM的长是( )
A、2个 B、3个 C、4个 D、5个12. 如图,将边长为9的正方形ABCD沿MN折叠,使点B落在CD边上的处,点A对应点为 , 且 , 则AM的长是( )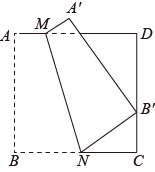 A、2 B、3 C、 D、
A、2 B、3 C、 D、二、填空题
-
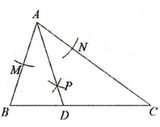
13. 计算: .14. 如图,在中, , 以点A为圆心,任意长为半径画弧,分别交AB、AC于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,若 , 则的度数是 .
 15. 已知点 , , 都在反比例函数的图象上,且 , 则 , , 的大小关系是 .16. 关于x的方程的解为 .17. 如图,将半径为2,圆心角为90°的扇形ABC绕A点逆时针旋转至点B的对应点点D落在弧AC上,则阴影部分的面积为 .
15. 已知点 , , 都在反比例函数的图象上,且 , 则 , , 的大小关系是 .16. 关于x的方程的解为 .17. 如图,将半径为2,圆心角为90°的扇形ABC绕A点逆时针旋转至点B的对应点点D落在弧AC上,则阴影部分的面积为 . 18. 如图,在正方形ABCD的对角线AC上取一点E,使得 , 连接BE并延长BE到F,使 , BF与CD相交于点H,若 , 有下列结论:①;②;③;④ , 则其中正确的结论有 . (填所有正确结论的序号)
18. 如图,在正方形ABCD的对角线AC上取一点E,使得 , 连接BE并延长BE到F,使 , BF与CD相交于点H,若 , 有下列结论:①;②;③;④ , 则其中正确的结论有 . (填所有正确结论的序号)
三、解答题
-
19. 先化简,再求值: , 其中x是不等式组的整数解.20. 在疫情防控期间,某中学为保障广大师生生命健康安全,预从商场购买一批免洗手消毒液和84消毒液,如果购买50瓶免洗手消毒液和100瓶84消毒液,共需花费1150元,如果购买40瓶免洗手消毒液和120瓶84消毒液,共需花费1080元.(1)、每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?(2)、经过协商,商场将免洗手消毒液按原价的8折卖给学校,84消毒液仍按原价,若学校购买两种消毒液共200瓶,且总花费不超过1500元,最多可购买多少瓶免洗手消毒液?21. 如图,在中,对角线AC的垂直平分线分别与AD、AC、BC交于点E、O、F.
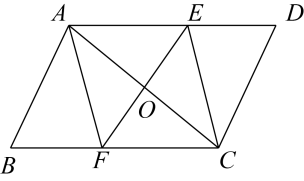 (1)、求证:四边形AFCE是菱形;(2)、若 , , 求四边形AFCE的面积.22. 为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据市场调查,在草莓上市销售的28天中,其销售价格m(元/公斤)与第x天之间满足(x为正整数),销售量n(公斤)与第x天之间的函数关系如图所示:
(1)、求证:四边形AFCE是菱形;(2)、若 , , 求四边形AFCE的面积.22. 为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据市场调查,在草莓上市销售的28天中,其销售价格m(元/公斤)与第x天之间满足(x为正整数),销售量n(公斤)与第x天之间的函数关系如图所示: (1)、求销售量n与第x天之间的函数关系式;(2)、求草莓上市销售第8天李大爷的销售收入;(3)、求草莓上市销售的第11天至14天这4天,每天的销售收入y与第x天之间的函数关系式;并求出这4天当中哪一天的销售额最高?为多少元?23. 如图,AB是的直径,AC是弦,于点D,过点A作的切线AP,与OD的延长线交于点P,连接CP,与AB的延长线交于点E.
(1)、求销售量n与第x天之间的函数关系式;(2)、求草莓上市销售第8天李大爷的销售收入;(3)、求草莓上市销售的第11天至14天这4天,每天的销售收入y与第x天之间的函数关系式;并求出这4天当中哪一天的销售额最高?为多少元?23. 如图,AB是的直径,AC是弦,于点D,过点A作的切线AP,与OD的延长线交于点P,连接CP,与AB的延长线交于点E.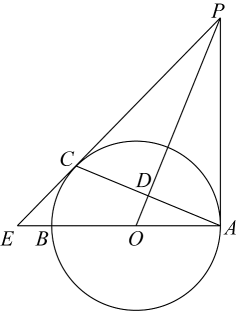 (1)、求证:PC是的切线;(2)、求证: .24. 如图所示,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是第三象限抛物线上的一个动点,连接DB与AC交于点E.
(1)、求证:PC是的切线;(2)、求证: .24. 如图所示,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是第三象限抛物线上的一个动点,连接DB与AC交于点E. (1)、求A、B、C三点坐标;(2)、如图1,连接BC,点D在运动过程中能否使得 , 若能,请求出点D的坐标,若不能,请说明理由;(3)、如图2,连接AD,过点D作x轴的垂线,垂足为点G,交AC于点H,设点D的横坐标为m
(1)、求A、B、C三点坐标;(2)、如图1,连接BC,点D在运动过程中能否使得 , 若能,请求出点D的坐标,若不能,请说明理由;(3)、如图2,连接AD,过点D作x轴的垂线,垂足为点G,交AC于点H,设点D的横坐标为m①用含有m的式子表示DH的长;
②和的面积分别为记为和 , 求的最大值.