安徽省全椒县2022年中考第二次模拟考试数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. |﹣2|的相反数为（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 袁隆平院士被誉为“杂交水稻之父”，经过他带领的团队多年艰苦努力，目前我国杂交水稻种植面积达2.4亿亩，每年增产的粮食可以养活8000万人．将数据8000万用科学记数法表示为 $8 \times 1 0^{n}$ ，则n的值为（）

A、7 B、8 C、9 D、10

查看试题解析
3. 如图所示的几何体是某圆柱体的一部分，切面是平面，则该几何体的俯视图为（）

A、 B、 C、 D、

查看试题解析
4. 下列计算结果为 $x^{6}$ 的是（）

A、 $x^{3} + x^{3}$ B、 $x \cdot x^{6}$ C、 $x^{12} \div x^{2}$ D、 $(- x^{3})^{2}$

查看试题解析
5. 如图，已知 $A B / / D E$ ，若 $∠ B = 120 °$ ， $∠ D = 20 °$ ，那么 $∠ B C D$ 的度数为（）

A、 $60 °$ B、 $70 °$ C、 $80 °$ D、 $100 °$

查看试题解析
6. 设 $6 - \sqrt{10}$ 的整数部分为a ，小数部分为b ，则 $(2 a + \sqrt{10}) b$ 的值是（）

A、6 B、 $2 \sqrt{10}$ C、12 D、 $9 \sqrt{10}$

查看试题解析
7. 某市2021年底有2万户5G用户，计划到2023年底全市5G用户数累计达到8.72万户．设全市5G用户数年平均増长率为x，则下列方程正确的是（）

A、2（1＋2x）＝8.72 B、2＋2（1＋x）＋2（1＋2x）＝8.72 C、2（1＋x）²＝8.72 D、2＋2（1＋x）＋2（1＋x）²＝8.72

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B = A C$ ， $△ D B C$ 和 $△ A B C$ 关于直线BC对称，连接AD ，与BC相交于点O ，过点C作 $C E ⊥ C D$ ，垂足为C ，与AD相交于点E ．若 $A D = 8$ ， $B C = 6$ ，则 $\frac{2 O E + A E}{B D}$ 的值为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{5}{3}$ D、 $\frac{5}{4}$

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 的系数具有这样的等差关系： $a - b = b - c$ ，且当 $x = 1$ 时， $y > 0$ ，则下列结论正确的是（）

A、 $b > 0 ， b^{2} - a c \geq 0$ B、 $b > 0 ， b^{2} - a c \leq 0$ C、 $b < 0 ， b^{2} - a c \geq 0$ D、 $b < 0 ， b^{2} - a c \leq 0$

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中，E是 $B D$ 的中点，则下列四个结论：① $A M = C N$ ；②若 $M D = A M$ ， $∠ A = 90 °$ ，则 $B M = C M$ ；③若 $M D = 2 A M$ ，则 $S_{△ M N C} = S_{△ B N E}$ ；④若 $A B = M N$ ，则 $△ M F N$ 与 $△ D F C$ 全等．其中正确结论的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 要使分式 $\frac{1}{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
12. 因式分解：x²－y（2x－y）＝．

查看试题解析
13. 如图，⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点，则∠AOC的度数为度.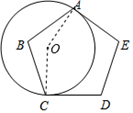

查看试题解析
14. 已知抛物线 $y = x^{2} - (m + 1) x + 2 m + 3$ ．

(1)、当m＝0时，点（2，4）（填“在”或“不在”）该抛物线上；

(2)、该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，该抛物线的顶点坐标为．

查看试题解析

三、解答题

15. 计算： $\sqrt{12} + | \sqrt{3} - 3 | - {(\frac{1}{3})}^{- 1} - t a n 60 °$ ．

查看试题解析
16. 如图，在由边长为1个单位长度的小正方形组成的网格中，给出了格点三角形ABC和格点O（网格线的交点，叫做格点）

(1)、作△ABC关于点O的中心对称图形△A₁B₁C₁；（点A，B，C的对应点分别为A₁ ， B₁ ， C₁）

(2)、将△A₁B₁C₁先向上平移5个单位长度，再向左平移1个单位长度，得到△A₂B₂C₂ ，画出△A₂B₂C₂；（点A₁ ， B₁ ， C₁的对应点分别为A₂ ， B₂ ， C₂）

(3)、连接OA，OC₂ ，则∠AOC₂＝°．

查看试题解析
17. 如图1是一台手机支架，图2是其侧面示意图，AB，BC可分别绕点A，B转动，测量知 $B C = 8 c m$ ， $A B = 16 c m$ .当AB，BC转动到 $∠ B A E = 60 °$ ， $∠ A B C = 50 °$ 时，求点C到AE的距离.（结果保留小数点后一位，参考数据： $s i n 70 ° \approx 0.94$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
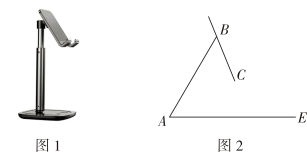18. 观察下列等式：
第1个等式： $(1 - \frac{1}{3}) \div \frac{4}{3} = \frac{1}{2}$ ；
第2个等式： $(1 - \frac{1}{4}) \div \frac{9}{8} = \frac{2}{3}$ ；
第3个等式： $(1 - \frac{1}{5}) \div \frac{16}{15} = \frac{3}{4}$ ；
第4个等式： $(1 - \frac{1}{6}) \div \frac{25}{24} = \frac{4}{5}$ ；
第5个等式： $(1 - \frac{1}{7}) \div \frac{36}{35} = \frac{5}{6}$ ；
……
按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第n个等式（用含n的等式表示），并证明．

查看试题解析
19. 如图，反比例函数 $y = \frac{k}{x}$ 的图像与一次函数y＝mx＋n的图像相交于点A（a，－1），B（－1，3）两点．

(1)、求反比例函数和一次函数的解析式；

(2)、设直线AB交y轴于点C，点N（t，0）是x轴正半轴上一点，过点N作NM⊥x轴交反比例函数 $y = \frac{k}{x}$ 的图像于点M，连接CN，OM，若 $S_{四边形 C O M N} = 3$ ，求t的值．

查看试题解析
20. 如图，AB是⊙O的直径，点C为⊙O上一点，连接AC，CN与⊙O相切， $O M ⊥ A B$ ，分别交AC，CN于点D，M．

(1)、试猜想线段MD与MC的数量关系，并说明理由；

(2)、连接BC，若AC＝6，∠B＝60°，求弧AC的长．

查看试题解析
21. 某校八年级开展“学党史”知识竞赛活动．为了解本次竞赛成绩，张老师随机抽取了部分参赛同学的成绩（均为整数）进行统计，并绘制成成绩等级分布表、成绩扇形统计图、频数分布直方图（每组含左端点不含右端点，最后一组含100），具体如下：
成绩等级分布表
等级
成绩x/分
A
a≤x≤100
B
80≤x＜a
C
60≤x＜80
D
0≤x＜60

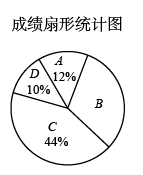
(1)、共抽取了名同学的成绩，频数分布直方图中，m＝， n＝；

(2)、已知在分数段90≤x≤100中的n名学生成绩的中位数为96分．强强同学的成绩为95分，则其成绩属于哪个等级？请说明理由；

(3)、A等级和B等级中各有3人参加“学党史”交流会，A等级的3人为2名男生，1名女生，B等级的3人为1名男生，2名女生．若从A等级和B等级参加“学党史”交流会的学生中分别随机选出1人分享学习经验，求选中的2人恰好为一男一女的概率．

查看试题解析
22. 甲秀楼是贵阳市一张靓丽的名片.如图①，甲秀楼的桥拱截面 $O B A$ 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽 $O A = 8 m$ ，桥拱顶点 $B$ 到水面的距离是 $4m$ .

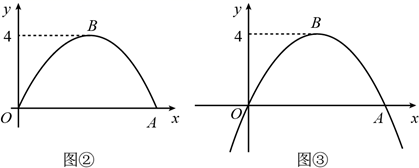(1)、按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；

(2)、一只宽为 $1 .2m$ 的打捞船径直向桥驶来，当船驶到桥拱下方且距 $O$ 点 $0 .4m$ 时，桥下水位刚好在 $O A$ 处.有一名身高 $1.68 m$ 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；

(3)、如图③，桥拱所在的函数图象是抛物线 $y = a x^{2} + b x + c (a \neq 0)$ ，该抛物线在 $x$ 轴下方部分与桥拱 $O B A$ 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 $m (m > 0)$ 个单位长度，平移后的函数图象在 $8 \leq x \leq 9$ 时， $y$ 的值随 $x$ 值的增大而减小，结合函数图象，求 $m$ 的取值范围.

查看试题解析
23. 探索并解决问题

(1)、【证明体验】如图1，AD为△ABC的角平分线，∠ADC＝60°，点E在线段AB上，AE＝AC，求证：DE平分∠ADB；

(2)、【思考探究】如图2，在（1）的条件下，F为AB上一点，连接FC交AD于点G．若FB＝FC，求证：DE²＝BD·DG；

(3)、【拓展延伸】如图3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA＝2∠DCA，点E在AC上，∠EDC＝∠ABC，若BC＝5， $C D = 2 \sqrt{5}$ ， AD＝2AE，求AC的长．

查看试题解析

等级	成绩x/分
A	a≤x≤100
B	80≤x＜a
C	60≤x＜80
D	0≤x＜60