安徽省六安市霍邱县2022年九年级第一次模拟考试数学试题

试卷更新日期：2022-06-08 类型：中考模拟

进入出卷网下载

一、单选题

1. -2022的绝对值是（）

A、 $- 2022$ B、 $2022$ C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 2022年2月4日—2月20日，第24届冬奥会在北京和张家口成功举行，中国冰雪运动参与人数达3.46亿，仅在2021年的北京，就有2.6万人经过培训成为冬季体育项目指导员，将3.46亿用科学记数法表示为（）

A、 $346 \times 1 0^{6}$ B、 $3.46 \times 1 0^{7}$ C、 $3.46 \times 1 0^{8}$ D、 $3.46 \times 1 0^{10}$

查看试题解析
3. 下列运算中，正确的是（）

A、 $4 a - 3 a = 1$ B、 $a^{2} \cdot a^{2} = 2 a^{2}$ C、 ${(a b^{2})}^{3} = a b^{6}$ D、 $a^{2} \cdot a^{4} = a^{6}$

查看试题解析
4. 如图是一个几何体的三种视图，则该几何体可能是（）

A、 B、 C、 D、

查看试题解析
5. 如图，把一副直角三角板如图那样摆放在平行直线AB，CD之间，∠EFG＝30°，∠MNP＝45°．则：① $E G ∥ P M$ ；②∠AEG＝45°；③∠BEF＝75°；④∠CMP＝∠EFN．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，有5张形状、大小、材质均相同的卡片，正面分别印着北京2022年冬奥会的越野滑雪、速度滑冰、花样滑冰、高山滑雪、单板滑雪大跳台的体育图标，背面完全相同．现将这5张卡片洗匀并正面向下放在桌上，从中随机抽取一张，抽出的卡片正面恰好是“滑冰”项目的图案的可能性是（）．

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 弹簧伸长的长度与所受拉力的大小成正比，某次实验中，小明记录了同一根弹簧的长度y（cm）和所挂重物的质量x（kg）（0≤x≤12）之间的部分对应数据如下表所示，下列说法中正确的是（）
x（kg）
0
0.5
1
1.5
2
…
y（cm）
10.5
11
11.5
12
…

A、x，y都是变量，y是x的正比例函数 B、当所挂重物的质量为5kg时，弹簧长度是14.5cm C、物体质量由5kg增加到7kg，弹簧的长度增加了1cm D、该弹簧不挂重物时的长度是10cm

查看试题解析
8. 若a＞b＞0，c＞d＞0，则下列式子不一定成立的是（）

A、a﹣c＞b﹣d B、 $\frac{c}{b} > \frac{d}{a}$ C、ac＞bc D、ac＞bd

查看试题解析
9. 某网店销售运动鞋，若每双盈利40元，每天可以销售20双，该网店决定适当降价促销，经调查得知，每双运动鞋每降价1元，每天可多销售2双，若想每天盈利1200元，并尽可能让利于顾客，赢得市场，则每双运动鞋应降价（）

A、10元或20元 B、20元 C、5元 D、5元或10元

查看试题解析
10. 如图，△ABC是等腰直角三角形，∠BAC＝90°，把一个三角尺的直角顶点与BC边的中点O重合，且两条直角边分别经过点A和点B．将三角尺绕点O按顺时针方向旋转任意一个锐角，设在旋转过程中三角尺的两直角边与AB，AC分别交于点E，F．有如下结论：①线段AE与AF的长度之和为定值；②∠BEO与∠OFC的度数之和为定值；③四边形AEOF的面积为定值；④四边形AEOF有外接圆，其中正确的有（）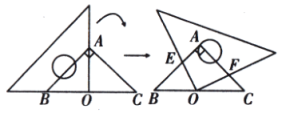

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. $\sqrt{9} + {(\frac{1}{3})}^{- 1} =$ ．

查看试题解析
12. 分解因式： $a b^{3} - 4 a b$ =.

查看试题解析
13. 如图，点A、B、C都在圆O上，O为圆心， $B C ∥ O A$ ，连接BO并延长，交圆O于点D，连接AC，DC，若∠A＝27°，则∠D＝°．

查看试题解析
14. 如图，Rt△ABC中，∠ACB＝90°，D、E分别为AB，BC边上一点，将△ACD、△BDE分别沿CD、DE折叠，A、B的对应点分别为 $A^{^{'}} 、 B^{^{'}}$ ，点 $B^{'}$ 恰好落在 $D A^{'}$ 上．

(1)、∠CDE＝°；

(2)、若 $\frac{D E}{C D} = \frac{D B}{A D}$ ，且 $D A^{'} ⊥ B C$ ， BC＝2，则BE的值为．

查看试题解析

三、解答题

15. 解不等式 $\frac{x - 1}{2} < \frac{4 x - 5}{3} - 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
16. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．

(1)、画出△ABC关于原点O的中心对称图形△A₁B₁C₁ ．

(2)、将△A₁B₁C₁绕点A₁逆时针旋转90°得到△A₁B₂C₂ ，画出△A₁B₂C₂ ，并直接写出点C₂的坐标．

查看试题解析
17. 某商场从安全和便利的角度出发，为提升顾客的购物体验，准备将自动扶梯由原来的阶梯式改造成斜坡式，如图，已知商场的层高AD为6m，坡角∠ABD为30°，改造后的斜坡式自动扶梯的坡角∠ACB为16°，请你计算改造后的自动扶梯增加的占地长度BC的长．（结果精确到0.1m，参考数据：sin16°≈0.28，cos16°≈0.96，tan16°≈0.29， $\sqrt{3} \approx 1.73$ ）

查看试题解析
18. 阅读下面的学习材料：我们知道，一般情况下式子； $\frac{m + n}{3 + 4}$ 与“ $\frac{m}{3} + \frac{n}{4}$ ”是不相等的（ $m$ ， $n$ 均为整数），但当 $m$ ， $n$ 取某些特定整数时，可以使这两个式子相等，我们把使“ $\frac{m + n}{3 + 4} = \frac{m}{3} + \frac{n}{4}$ ”成立的数对“ $m$ ， $n$ ”叫做“好数对”，记作 $[m ， n]$ ，例如，当 $m = n = 0$ 时，有 $\frac{m + n}{3 + 4} = \frac{m}{3} + \frac{n}{4}$ 成立，则数对“0，0”就是一对“好数对”，记作[0，0]
解答下列问题：

(1)、通过计算，判断数对“3，4”是否是“好数对”；

(2)、求“好数对” $[x ， - 32]$ 中 $x$ 的值；

(3)、请再写出一对“好数对”[9，_]；

(4)、对于“好数对” $[a ， b]$ ，如果 $a = 9 k$ （ $k$ 为整数），则 $b =$ （用含 $k$ 的代数式表示）．

查看试题解析
19. 如图，一次函数y＝kx+b的图象与反比例函数y＝ $\frac{m}{x}$ 的图象相交于A（1，2），B（﹣2，n）两点．

(1)、求一次函数和反比例函数的表达式；

(2)、直线AB交x轴于点C，点P是x轴上的点，若△ACP的面积是4，求点P的坐标．

查看试题解析
20. 如图，已知AB为☉O的直径，AC，CD是弦．AB⊥CD于E．OF⊥AC于F．连接BC．

(1)、求证： $O F ∥ B C$ ；

(2)、若BE＝2cm， $C D = 4 \sqrt{3} c m$ ，求AC的长．

查看试题解析
21. 为了了解某地区初中学生每天课外阅读所用的时间情况，从该地区各初中学校中随机抽取了一部分学生进行问卷调查，并将结果绘制成如下不完整的频数分布表和频数分布直方图．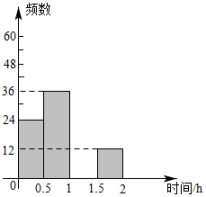
每天课外阅读的时间t/h
频数
频率
0<t≤0.5
24
0.5<t≤1
36
0.3
1<t≤1.5
0.4
1.5<t≤2
12
b
合计
a
1
根据以上信息，回答问题：

(1)、表中a＝， b＝；

(2)、请补全频数分布直方图；

(3)、若该地区初中学生总数为6480人，试估计该地区初中学生每天课外阅读时间不超过1小时的人数．

查看试题解析
22. 如图1，在平面直角坐标系中，已知C点坐标为（0，-3），且OA＝OC＝3OB，抛物线 $y = a x^{2} + b x - 3 (a \neq 0)$ 图象经过A，B，C三点，D点是该抛物线的顶点．

(1)、求抛物线所对应的函数表达式；

(2)、判断△ADC的形状，并求△ADC的面积；

(3)、如图2，点P是该抛物线位于第三象限的部分上的一个动点，过P点作PE⊥AC于点E，PE的值是否存在最大值？如果存在，请求出PE的最大值；如果不存在，请说明理由．

查看试题解析
23. 如图1，在正方形ABCD中，E为AD边上一点，CO⊥BE交AB于F．EF交CB延长线于G．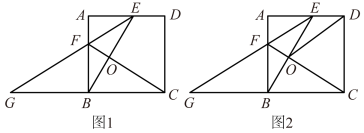

(1)、当E为AD中点时，求证：BC＝2BG；

(2)、如图2，当BG＝BC时，求证： $A E^{2} = A F \cdot A B$ ；

(3)、在（2）的条件下，连接OD，求tan∠EOD的值．

查看试题解析

每天课外阅读的时间t/h	频数	频率
0<t≤0.5	24
0.5<t≤1	36	0.3
1<t≤1.5		0.4
1.5<t≤2	12	b
合计	a	1

x（kg）	0	0.5	1	1.5	2	…
y（cm）		10.5	11	11.5	12	…