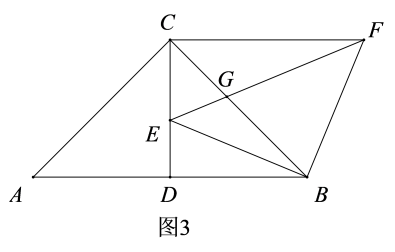安徽省合肥市瑶海区2022年中考二模数学试题
试卷更新日期:2022-06-08 类型:中考模拟
一、单选题
-
1. -3的相反数是( )A、 B、-3 C、3 D、2. 下列计算正确的是( )A、a3+a2=a5 B、a3•a2=a5 C、(a2)3=a5 D、a10÷a2=a53. 如图是一个工件的模型,其左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 中国科学院古脊椎动物与古人类研究所(中科院古脊椎所)2022年3月30日发布一项最新化石发现及研究,该所科研团队在江西武宁县一处志留纪地层中首次发现早期真盔甲鱼类的两个新属种化石,命名“俊卿清水鱼”和“刺猬安吉鱼”.距今约438 000 000年,代表了迄今最古老、最原始的真盔甲鱼类化石记录,将438 000 000用科学记数法表示为( )A、438×106 B、43.8×107 C、4.38×108 D、4.38×1075. 下列一元二次方程中,没有实数根的是( )A、x2-2x-3=0 B、(x-2)(x+3)=0 C、x2=5 D、x2-2x+3=06. 已知,如图,点C是以AB为直径的半圆O上一点,过点C作⊙O的切线CD,BD⊥CD于点D,若∠DCB=50°,则∠ABC的度数是( )
4. 中国科学院古脊椎动物与古人类研究所(中科院古脊椎所)2022年3月30日发布一项最新化石发现及研究,该所科研团队在江西武宁县一处志留纪地层中首次发现早期真盔甲鱼类的两个新属种化石,命名“俊卿清水鱼”和“刺猬安吉鱼”.距今约438 000 000年,代表了迄今最古老、最原始的真盔甲鱼类化石记录,将438 000 000用科学记数法表示为( )A、438×106 B、43.8×107 C、4.38×108 D、4.38×1075. 下列一元二次方程中,没有实数根的是( )A、x2-2x-3=0 B、(x-2)(x+3)=0 C、x2=5 D、x2-2x+3=06. 已知,如图,点C是以AB为直径的半圆O上一点,过点C作⊙O的切线CD,BD⊥CD于点D,若∠DCB=50°,则∠ABC的度数是( ) A、25° B、40° C、45° D、50°7. 已知直线y=-4x-6经过点(m,n),且2m-7n≤0,则下列关系式正确的是( )A、 B、 C、 D、8. 在合肥著名的旅游景点三河古镇、安徽博物院、合肥渡江战役纪念馆、包公园中小明选择的是合肥渡江战役纪念馆和包公园.若小明让好朋友小聪从中选择两个最想去的景点,则小聪正好选择和小明相同景点的概率是( )A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D,则cosA=( )
A、25° B、40° C、45° D、50°7. 已知直线y=-4x-6经过点(m,n),且2m-7n≤0,则下列关系式正确的是( )A、 B、 C、 D、8. 在合肥著名的旅游景点三河古镇、安徽博物院、合肥渡江战役纪念馆、包公园中小明选择的是合肥渡江战役纪念馆和包公园.若小明让好朋友小聪从中选择两个最想去的景点,则小聪正好选择和小明相同景点的概率是( )A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D,则cosA=( ) A、 B、 C、 D、10. 已知△ABC是等边三角形,点D是AB边上一点,连接CD,以CD为边作等边△DEC交BC于点F,连接BE,点M是BC的中点,连接EM,则下列结论错误的是( )A、△ADC≌△BEC B、若CD平分∠ACB,则BD=BE C、若AB=2,则ME长度的最小值是 D、若BD:AD=1:2,则BF:FC=1:4
A、 B、 C、 D、10. 已知△ABC是等边三角形,点D是AB边上一点,连接CD,以CD为边作等边△DEC交BC于点F,连接BE,点M是BC的中点,连接EM,则下列结论错误的是( )A、△ADC≌△BEC B、若CD平分∠ACB,则BD=BE C、若AB=2,则ME长度的最小值是 D、若BD:AD=1:2,则BF:FC=1:4二、填空题
-
11. 计算:(-1)-= .12. 不等式组 的解集是 .13. 如图,过反比例函数(x>0)的图像上一点A作AB⊥x轴于点B,点C在y轴上,OB=OC= , 连接AC,过点C作CD⊥AB于点D,若S△ACD=S四边形OBDC,则k的值为 .
 14. 已知,矩形ABCD中,AB=2,BC=4,点E是对角线BD上一点,连接AE并延长交矩形的一边于点F,将△ABF沿直线AF翻折,使得点B落在处.(1)若∠BAE=30°,则=;(2)若AE=2EF,则的长为 .
14. 已知,矩形ABCD中,AB=2,BC=4,点E是对角线BD上一点,连接AE并延长交矩形的一边于点F,将△ABF沿直线AF翻折,使得点B落在处.(1)若∠BAE=30°,则=;(2)若AE=2EF,则的长为 .三、解答题
-
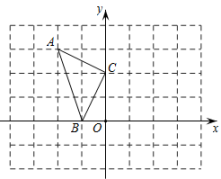
15. 解方程组 .16. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,3)、B(-1,0)、C(0,2).
 (1)、请在图中画出△ABC关于y轴对称的△A1B1C1;(2)、以点B为旋转中心,将△ABC逆时针旋转到△A2BC2 , 使得点A的对应点A2坐标为(-4,1),在图中画出△A2BC2 .17. 观察以下等式:第1个等式:;第2个等式:;
(1)、请在图中画出△ABC关于y轴对称的△A1B1C1;(2)、以点B为旋转中心,将△ABC逆时针旋转到△A2BC2 , 使得点A的对应点A2坐标为(-4,1),在图中画出△A2BC2 .17. 观察以下等式:第1个等式:;第2个等式:;第3个等式:;第4个等式:;……;
按照以上规律,解答下列问题:
(1)、写出第5个等式: ;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.18. 2021年底中国高铁运营里程数已达4万公里,中国高铁发展速度之快、质量之高令全世界惊叹,是当之无愧的“国家名片”.如图所示某条高铁路基的横断面是四边形ABCD,ADBC,路基顶BC宽10米,斜坡AB长为15米,斜坡AB的坡角α是32°,斜坡CD的坡度i=1:2.5,求路基底AD的长.(结果精确到1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)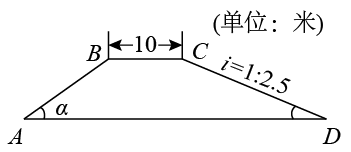 19. 随着我国数字化阅读方式的接触率和人群持续增多,数字阅读凭借独有的便利性成为了更快获得优质内容的重要途径,目前,数字阅读已经成为当下更环保、更年轻的阅读方式,2019年中国数字阅读市场规模为293亿元,2021年为421.92亿元.(1)、求2019到2021年中国数字阅读市场规模的年平均增长率;(2)、预计2022年中国数字阅读市场规模是否可以达到510亿元?20. 已知,如图,△ABC内接于⊙O,CD是直径,过点C作CE⊥AB于点E,点G是AB的中点,连接OG,过点D作DF⊥AB于点F,连接DE.
19. 随着我国数字化阅读方式的接触率和人群持续增多,数字阅读凭借独有的便利性成为了更快获得优质内容的重要途径,目前,数字阅读已经成为当下更环保、更年轻的阅读方式,2019年中国数字阅读市场规模为293亿元,2021年为421.92亿元.(1)、求2019到2021年中国数字阅读市场规模的年平均增长率;(2)、预计2022年中国数字阅读市场规模是否可以达到510亿元?20. 已知,如图,△ABC内接于⊙O,CD是直径,过点C作CE⊥AB于点E,点G是AB的中点,连接OG,过点D作DF⊥AB于点F,连接DE. (1)、求证:CA•CB=CD•CE;(2)、若∠ABC=45°,AE=1、BC=3 , 求OG的长.21. 为迎接2022年世界乒乓球职业大联盟(WTT)比赛的到来,某企业推出了A、B两种乒乓球新产品,为了解两种新产品的质量情况(固度、硬度、弹跳高度等)进行了抽样调查,在相同条件下,随机抽取了两种产品各8组样品。对每组样品的质量进行综合评分(10分制),下面给出两种产品8组样品质量得分的统计图表.
(1)、求证:CA•CB=CD•CE;(2)、若∠ABC=45°,AE=1、BC=3 , 求OG的长.21. 为迎接2022年世界乒乓球职业大联盟(WTT)比赛的到来,某企业推出了A、B两种乒乓球新产品,为了解两种新产品的质量情况(固度、硬度、弹跳高度等)进行了抽样调查,在相同条件下,随机抽取了两种产品各8组样品。对每组样品的质量进行综合评分(10分制),下面给出两种产品8组样品质量得分的统计图表.
A、B两种乒乓球新产品得分表
组号
1
2
3
4
5
6
7
8
A种产品(分)
8.2
8.4
9.0
8.5
9.0
9.2
9.0
9.1
B种产品(分)
7.5
8.2
8.5
8.8
9.0
9.6
9.6
9.2
A、B两种乒乓球新产品得分统计表
平均数
中位数
众数
A种产品
8.8
9.0
a
B种产品
8.8
b
9.6
(1)、a=;b=;(2)、补全折线统计图,并分析哪种产品的得分比较稳定;(3)、小聪认为A种乒乓球新产品的质量好,小明认为B种乒乓球新产品的质量好,请你结合统计图表中的信息分别写出他们说法的理由.22. 已知二次函数y=ax+ax+c(a≠0).(1)、若它的图象经过点(-1,0)、(1,2),求函数的表达式;(2)、若a<0,当-1≤x<4时,求函数值y随x的增大而增大时x的取值范围;(3)、若a=1、c=-2,点(m,n)在直线y=x-2上,求当x=m,n时的二次函数的函数值和的最小值.23. 已知,在△ABC中,∠ACB=90°,AC=BC,CD是AB边上的中线,点E为CD上一点,连接BE,作FB⊥BE,且FB=EB,连接FE和FC,FE交BC于点G.(1)、如图1,若点E与点D重合,求证:点G是BC的中点; (2)、如图2,求证:CF//AB;
(2)、如图2,求证:CF//AB; (3)、如图3,若BE平分∠DBC,AB=2,求CG:BC的值.
(3)、如图3,若BE平分∠DBC,AB=2,求CG:BC的值.