(北师大版)2021-2022学年度第二学期八年级数学2.3不等式的解集 期末复习测试卷
试卷更新日期:2022-06-08 类型:复习试卷
一、单选题
-
1. 不等式组的解集在数轴上应表示为( )A、
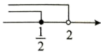 B、
B、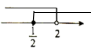 C、
C、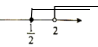 D、
D、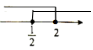 2. 如图,数轴上表示的是下列哪个不等式组的解集( )
2. 如图,数轴上表示的是下列哪个不等式组的解集( )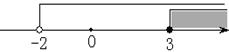 A、 B、 C、 D、3. 已知两个不等式的解集在数轴上如右图表示,那么这个解集为( )
A、 B、 C、 D、3. 已知两个不等式的解集在数轴上如右图表示,那么这个解集为( )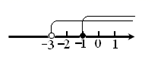 A、x≥-1 B、
A、x≥-1 B、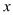 >1
C、-3<x≤-1
D、x>-3
4. 下列说法不正确的是( )A、是不等式的一个解 B、是不等式的一个解集 C、与的解集不相同 D、与的解集相同5. 如图,将两个关于x的一元一次不等式的解集表示在同一数轴上则这两个不等式的公共解集为( )
>1
C、-3<x≤-1
D、x>-3
4. 下列说法不正确的是( )A、是不等式的一个解 B、是不等式的一个解集 C、与的解集不相同 D、与的解集相同5. 如图,将两个关于x的一元一次不等式的解集表示在同一数轴上则这两个不等式的公共解集为( )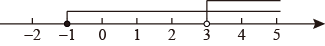 A、x≥﹣1 B、x>3 C、﹣1≤x<3 D、x<36. 若关于 的不等式 的解集是 ,则m的取值范围是( )A、 B、m>1 C、m<1 D、 为任何实数7. 已知关于x的不等式3x-m+1>0的最小整数解为2,则实数m的取值范围是( )A、4<m<7 B、4≤m<7 C、4<m≤7 D、4≤m≤78. 已知关于x的不等式(1-a)x>1的解集为x< ,则a的取值范围是( )A、a≥1 B、0≤a<1 C、a>1 D、0<a≤19. 如果不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、10. 如图,天平右盘中的每个砝码的质量为10g,则物体M的质量m(g)的取值范围在数轴上可表示为( )
A、x≥﹣1 B、x>3 C、﹣1≤x<3 D、x<36. 若关于 的不等式 的解集是 ,则m的取值范围是( )A、 B、m>1 C、m<1 D、 为任何实数7. 已知关于x的不等式3x-m+1>0的最小整数解为2,则实数m的取值范围是( )A、4<m<7 B、4≤m<7 C、4<m≤7 D、4≤m≤78. 已知关于x的不等式(1-a)x>1的解集为x< ,则a的取值范围是( )A、a≥1 B、0≤a<1 C、a>1 D、0<a≤19. 如果不等式组 的解集是 ,则a的取值范围是( )A、 B、 C、 D、10. 如图,天平右盘中的每个砝码的质量为10g,则物体M的质量m(g)的取值范围在数轴上可表示为( ) A、
A、 B、
B、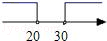 C、
C、 D、
D、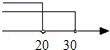
二、填空题
-
11. 若关于 的不等式 的正整数解只有3个,则 的取值范围是 .12. 写一个解集为x<-4的不等式为.13. 不等式x+3>5的解集为 .14. 如图,在平面直角坐标系xOy中,一次函数 与反比例函数 的图象交于点 , .结合图象,直接写出关于x的不等式 的解集
 15. 如果1<x<2,则(x﹣1)(x﹣2)0.(填写“>”、“<”或“=”)
15. 如果1<x<2,则(x﹣1)(x﹣2)0.(填写“>”、“<”或“=”)三、解答题
-
16. 解不等式组: ,并在数轴上表示不等式组的解集.17. 若方程(m+2)x=2的解为x=2,想一想,直接写出不等式(2-m)x<3的解集,并探究-2,-1,0,1,2这五个数中哪些数是该不等式的解?哪些数不是该不等式的解?
18. 是否存在整数m,使关于x的不等式1+>+与关于x的不等式x+1> 的解集相同?若存在,求出整数m和不等式的解集;若不存在,请说明理由.19. 已知方程组 的解满足x为非正数,y为负数.(1)求m的取值范围;
(2)化简:|m﹣3|﹣|m+2|;
(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1.
20. 已知一元一次不等式mx﹣3>2x+m.(1)若它的解集是x< , 求m的取值范围;
(2)若它的解集是x , 试问:这样的m是否存在?如果存在,求出它的值;如果不存在,请说明理由.
21. 已知关于x的不等式(2a﹣b)x+a﹣5b>0的解集为x< ,(1)求的值.
(2)求关于x的不等式ax>b的解集.
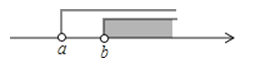
22. (1)不等式组有解,求利用数轴m的取值范围.(2)表示不等式组的解集如图所示,求不等式组的解集.
 23.
23.请阅读求绝对值不等式|x|<3和|x|>3的解集的过程:
因为|x|<3,从如图1所示的数轴上看:大于﹣3而小于3的数的绝对值是小于3的,
所以|x|<3的解集是﹣3<x<3;
因为|x|>3,从如图2所示的数轴上看:小大于﹣3的数和大于3的数的绝对值是大于3的,
所以|x|>3的解集是x<﹣3或x>3.

解答下面的问题:
(1)不等式|x|<a(a>0)的解集为多少?;不等式|x|>a(a>0)的解集为多少?
(2)解不等式|x﹣5|<3;
(3)解不等式|x﹣3|>5.