(北师大版)2021-2022学年度第二学期八年级数学第一章三角形的证明 期末复习测试卷
试卷更新日期:2022-06-07 类型:复习试卷
一、单选题
-
1. 如图,在 中,以点O为圆心,任意长为半径作弧,分别交该角的两边于 两点,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,连结OC,若 ,则 的度数是 ( )
 A、 B、 C、 D、2. 如图,△ABC中,AB=6,AC=8,∠ABC与∠ACB的平分线BD、CD交于点D.过点D作EF∥BC,分别交AB,AC于点E,F,则△AEF的周长为( )
A、 B、 C、 D、2. 如图,△ABC中,AB=6,AC=8,∠ABC与∠ACB的平分线BD、CD交于点D.过点D作EF∥BC,分别交AB,AC于点E,F,则△AEF的周长为( )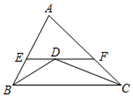 A、12 B、13 C、14 D、153. 如图,在 中, , 、 、 分别是各边延长线的点, ,则 的度数为( )
A、12 B、13 C、14 D、153. 如图,在 中, , 、 、 分别是各边延长线的点, ,则 的度数为( ) A、 B、 C、 D、4. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,BD=1,则AB的长度是( )
A、 B、 C、 D、4. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,BD=1,则AB的长度是( )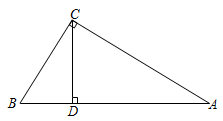 A、8 B、6 C、4 D、25. 如图,四边形 中, , , ,点M是对角线 的中点,点N是 边的中点,连结 , ,若 ,则线段 的长是( )
A、8 B、6 C、4 D、25. 如图,四边形 中, , , ,点M是对角线 的中点,点N是 边的中点,连结 , ,若 ,则线段 的长是( )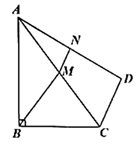 A、 B、3 C、 D、56. 如图在Rt△ABC中,∠ACB=90°,AB=10cm,点D是AB的中点,则CD的长度是( )
A、 B、3 C、 D、56. 如图在Rt△ABC中,∠ACB=90°,AB=10cm,点D是AB的中点,则CD的长度是( ) A、7cm B、6cm C、5cm D、4cm7. 已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )A、
A、7cm B、6cm C、5cm D、4cm7. 已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )A、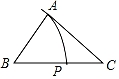 B、
B、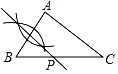 C、
C、 D、
D、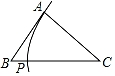 8. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点E,交BC于点F,连接AF,若∠FAC=∠B,则∠FAB的度数为( )
8. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点E,交BC于点F,连接AF,若∠FAC=∠B,则∠FAB的度数为( ) A、25° B、30° C、35° D、50°9. 如图,在 中, ,作 的垂直平分线,交 于点 ,交 于点 ,若 ,则 的长度是( )
A、25° B、30° C、35° D、50°9. 如图,在 中, ,作 的垂直平分线,交 于点 ,交 于点 ,若 ,则 的长度是( ) A、3 B、2 C、 D、10. 如图, , , , 若 , 则为( )
A、3 B、2 C、 D、10. 如图, , , , 若 , 则为( )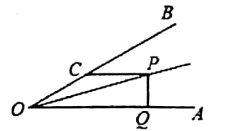 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,已知△ABC是等边三角形, ∠BCD =90°,BC=CD,则∠BAD=
 12. 如图,在 中, 分别是 上的任意一点,求 的最小值为.
12. 如图,在 中, 分别是 上的任意一点,求 的最小值为. 13. 如图,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD=.
13. 如图,在△ABC中,∠A=40°,∠B=90°,线段AC的垂直平分线MN与AB交于点D,与AC交于点E,则∠BCD=. 14. 如图所示,在矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E,F,连结CE,则CE的长为.
14. 如图所示,在矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E,F,连结CE,则CE的长为. 15. 如图、∠ABC的平分线BF与△ABC中∠ACB的外角∠ACG的平分线CF相交于点F.过F作DF∥BC,交AB于D,交AC于E,若BD=8,DE=3,则CE的长度为;
15. 如图、∠ABC的平分线BF与△ABC中∠ACB的外角∠ACG的平分线CF相交于点F.过F作DF∥BC,交AB于D,交AC于E,若BD=8,DE=3,则CE的长度为;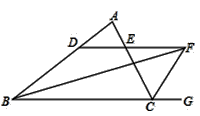
三、解答题
-
16. 已知等腰三角形ABC中,AB=AC=cm,底边BC=cm,求底边上的高AD的长.17. 如图,在 中,∠ABC和∠ACB的平分线交于点E,过点E作MN BC交AB于M,交AC于N,求证: 为等腰三角形.
 18. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠ACD=3∠BCD,点E是AB的中点.求∠CED的度数.
18. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠ACD=3∠BCD,点E是AB的中点.求∠CED的度数. 19. 如图,在△ABC中,点D , E分别是边AB , AC的中点,AF⊥BC , 垂足为点F , ∠ADE=30°,DF=3, ,求FC的长度.
19. 如图,在△ABC中,点D , E分别是边AB , AC的中点,AF⊥BC , 垂足为点F , ∠ADE=30°,DF=3, ,求FC的长度. 20. 在△ABC中,AB= AC,∠BAC=120°,AB边的垂直平分线交AB于D,交BC于E,求证: BE= CE.
20. 在△ABC中,AB= AC,∠BAC=120°,AB边的垂直平分线交AB于D,交BC于E,求证: BE= CE.