（北师大版）2021-2022学年度第二学期八年级数学1.4角平分线 期末复习测试卷
试卷更新日期：2022-06-07 类型：复习试卷
一、单选题
-
1. 如图，三条公路把A，B，C三个村庄连成一个三角形区域，某地区决定在这个三角形区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，则这个集贸市场应建在（ ）
A、三个角的角平分线的交点 B、三条边的垂直平分线的交点 C、三角形三条高的交点 D、三角形三条中线的交点2. 如图，在 中， ， ， 平分 交 于点 ， ，垂足为 .若 ，则 的长为（ ）
A、 B、 C、 D、63. 如图，AE与BF交于点O，点O在CG上，根据尺规作图的痕迹，判断下列说法错误的是（ ）
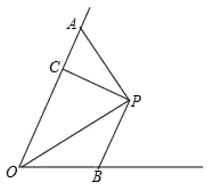
A、AE、BF是△ABC的内角平分线 B、CG也是△ABC的一条内角平分线 C、AO＝BO＝CO D、点O到△ABC三边的距离相等4. 如图，已知∠ABC，小彬借助一把没有刻度且等宽的直尺，按如图的方法画出了∠ABC的平分线BP．他这样做的依据是（ ）
A、在一个角的内部，且到角两边的距离相等的点在这个角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、测量垂直平分线上的点到这条线段的距离相等5. 如图，点P是∠AOC的角平分线上一点，PD⊥OA，垂足为点D，且PD＝3，点M是射线OC上一动点，则PM的最小值为（ ）
A、2 B、3 C、4 D、56. 内一点 到三边距离相等，则点 一定是 （ ）A、三条角平分线的交点 B、三边垂直平分线的交点 C、三条高的交点 D、三条中线的交点7. 如图，在 中， ， 为 的角平分线.若 ，则点 到 的距离为（ ）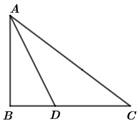
A、3 B、4 C、5 D、68. 如图，在 中， 平分 交 于 ，垂足为 .若 则点 到 的距离为（ ）
A、 B、 C、2 D、9. 如图，在 中， 于 ， 于 ，并且 ， 为 上一点．则下列结论中正确的是（ ）
A、 B、 C、 D、10. 如图，已知P是∠AOB的平分线上的一点，∠AOB＝60°，PD⊥OA，M是OP的中点，点C是OB上的一个动点，若PC的最小值为3 cm，则MD的长度为( )
A、3cm B、3 cm C、2cm D、2 cm二、填空题
-
11. 如图，已知∠AOP=15°，OP平分∠AOB，PC∥OB，PD⊥OB，如果PC=8，那么PD = .
12. 如图，在 中， 是 的角平分线， ，垂足为E，若 .
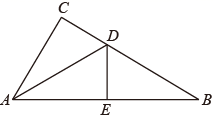13. 如图，四边形ABCD中，∠B＋∠D＝180°，AC平分∠DAB，CM⊥AB于点M，若AM＝4cm，BC＝2.5cm，则四边形ABCD的周长为cm．
14. 如图，OP平分∠AOB ， PC⊥OA ， 点D是OB上的动点，若PC＝1cm，则PD的长的最小值为 ．
15. 如图，在△ABC中，∠B＝30°，AC= ，边AB的垂直平分线分别交AB和BC与点E ， D ， 且AD平分∠BAC则DE的长度为 ．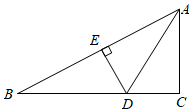
三、解答题
-
16. 如图，AD 是∠BAC 的平分线，DE⊥AB 于E，DF ⊥AC于F，且BD =CD.求证：BE =CF.
17. 如图，在△ABC中，AD是它的角平分线，且BD＝CD，DE⊥AB，DF⊥AC，垂足分别为E，F.求证：EB＝FC.
18. 如图， 是 的角平分线， 于点B， 于点C，D是 上一点.求证： .
19. 如图，在△ABC中，∠BAC＝90°，AD⊥BC于点D ， ∠ACB的平分线交AD于点E ， 交AB于点F ， FG⊥BC于点G ． 求证：AE＝FG ．
20. 如图，在△ABC中，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，BD=DC，求证：∠B=∠C
