(北师大版)2021-2022学年度第二学期八年级数学1.3线段的垂直平分线 期末复习测试卷
试卷更新日期:2022-06-07 类型:复习试卷
一、单选题
-
1. 某公园的A,B,C处分别有海资船、摩天轮、旋转木马三个娱乐项目,现要在公园内一个售票中心,使三个娱乐项目所处位置到售票中心的距离相等,则售票中心应建立在( )
 A、△ABC三边高线的交点处 B、△ABC三角角平分线的交点处 C、△ABC三边中线的交点处 D、△ABC三边垂直平分线的交点处2. 如图,在 ABC中,∠ACB=90°,分别以A,B为圆心,以大于 AB的长为半径作弧,两弧分别交于M,N两点,作直线MN交AB于点D,交AC于点F,连接BF,下列结论不一定成立的是( )
A、△ABC三边高线的交点处 B、△ABC三角角平分线的交点处 C、△ABC三边中线的交点处 D、△ABC三边垂直平分线的交点处2. 如图,在 ABC中,∠ACB=90°,分别以A,B为圆心,以大于 AB的长为半径作弧,两弧分别交于M,N两点,作直线MN交AB于点D,交AC于点F,连接BF,下列结论不一定成立的是( )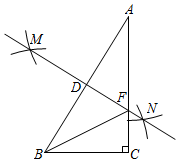 A、BF=AF B、∠CBF=90°﹣2∠A C、∠ABF=∠FBC D、 ADF≌ BDF3. 如图所示,在已知的 中,按以下步骤作图:①分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于两点 , ;②作直线 交 于点 ,连接 .若 , ,则 的度数为( )
A、BF=AF B、∠CBF=90°﹣2∠A C、∠ABF=∠FBC D、 ADF≌ BDF3. 如图所示,在已知的 中,按以下步骤作图:①分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于两点 , ;②作直线 交 于点 ,连接 .若 , ,则 的度数为( )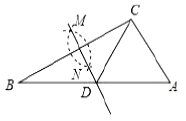 A、95° B、100° C、105° D、110°4. 如图,△ABC,AB=AC,∠B=40°,边AC的垂直平分线DE交AC、BC于点D、E,连接EA.则∠BAE的度数为( )
A、95° B、100° C、105° D、110°4. 如图,△ABC,AB=AC,∠B=40°,边AC的垂直平分线DE交AC、BC于点D、E,连接EA.则∠BAE的度数为( )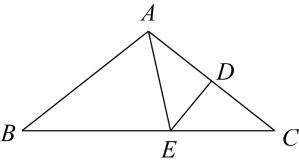 A、 B、 C、 D、5. 在联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边中垂线的交点6. 在中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )A、30° B、40° C、50° D、60°7. 如图,在等边三角形中,边上的高 , 是高上的一个动点,是边的中点,在点运动的过程中,存在的最小值,则这个最小值是( )
A、 B、 C、 D、5. 在联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边中垂线的交点6. 在中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC的度数为( )A、30° B、40° C、50° D、60°7. 如图,在等边三角形中,边上的高 , 是高上的一个动点,是边的中点,在点运动的过程中,存在的最小值,则这个最小值是( )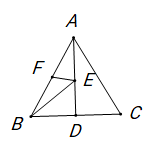 A、5 B、6 C、7 D、88. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交AC于点D,交BC于点E,交BA的延长线于点F,若 ,则BF的长为( )
A、5 B、6 C、7 D、88. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交AC于点D,交BC于点E,交BA的延长线于点F,若 ,则BF的长为( )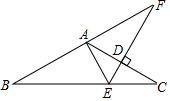 A、 B、3 C、 D、9. 如图所示,在△ABC中, , , DE为AB的中垂线, , 则CD的长是( )
A、 B、3 C、 D、9. 如图所示,在△ABC中, , , DE为AB的中垂线, , 则CD的长是( ) A、3 B、4 C、6 D、810. 如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( )
A、3 B、4 C、6 D、810. 如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( ) A、72° B、100° C、108° D、120°
A、72° B、100° C、108° D、120°二、填空题
-
11. 如图,在△ABC中,AB=AC=10,BC=12,点D是边BC的中点,直线MN是AB的垂直平分线,点E是MN上的一个动点,则△BDE周长的最小值是 .
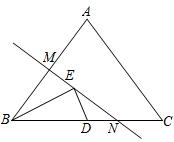 12. 在中, , AB的垂直平分线交AB于点D,交直线AC于点E, , 那么等于 .13. 如图,已知在中, , 边AB的垂直平分线交AC于点E,和的周长分别是28cm和18cm,则AB的长为cm.
12. 在中, , AB的垂直平分线交AB于点D,交直线AC于点E, , 那么等于 .13. 如图,已知在中, , 边AB的垂直平分线交AC于点E,和的周长分别是28cm和18cm,则AB的长为cm.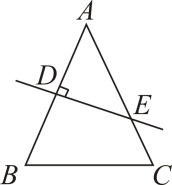 14. 如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是 .
14. 如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是 .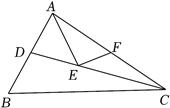 15. 如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=6cm,∠B=15°,则AC等于.
15. 如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=6cm,∠B=15°,则AC等于.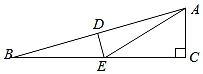
三、解答题
-
16. 如图,在中, , 是的垂直平分线,恰好平分 . 若 , 求的长.
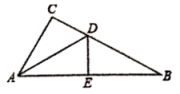 17. 如图,在中, , 的垂直平分线交于点C,且 .
17. 如图,在中, , 的垂直平分线交于点C,且 .求:的度数.
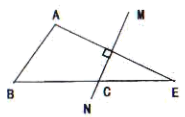 18. 如图,在△ABC 中,∠BAC =80°,AB、AC 的垂直平分线分别与BC 交于 D、E,求∠EAD 的度数。
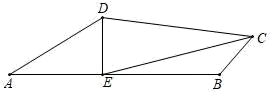
18. 如图,在△ABC 中,∠BAC =80°,AB、AC 的垂直平分线分别与BC 交于 D、E,求∠EAD 的度数。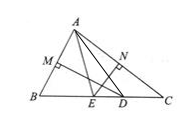 19. 如图,在三角形ABC中,DE是AC边的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=30°,求证:△ABD是等边三角形.
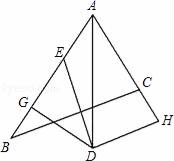
19. 如图,在三角形ABC中,DE是AC边的垂直平分线,且分别交BC、AC于点D和E,∠B=60°,∠C=30°,求证:△ABD是等边三角形.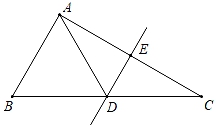 20. 如图,△ABC中,∠CAB的平分线与BC的垂直平分线DG相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.
20. 如图,△ABC中,∠CAB的平分线与BC的垂直平分线DG相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.