(北师大版)2021-2022学年度第二学期八年级数学1.2直角三角形 期末复习测试卷
试卷更新日期:2022-06-07 类型:复习试卷
一、单选题
-
1. 直角三角形的斜边长为10,则斜边上的中线长为( )A、2 B、3 C、4 D、52. 如图,Rt△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,AD=10,则点D到AB的距离是( )
 A、8 B、5 C、6 D、43. 如果三角形一边上的中线等于这条边的一半,那么这个三角形一定是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、不确定4. 如图,中, , , 于, , 的长度是( )
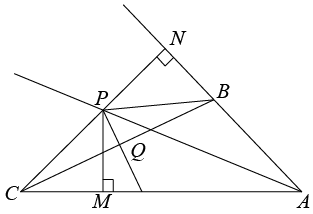
A、8 B、5 C、6 D、43. 如果三角形一边上的中线等于这条边的一半,那么这个三角形一定是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、不确定4. 如图,中, , , 于, , 的长度是( )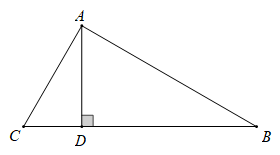 A、 B、 C、 D、无法确定5. 如图,在中, , , , BD是的角平分线,点P,点N分别是BD,AC边上的动点,点M在BC上,且 , 则的最小值为( )
A、 B、 C、 D、无法确定5. 如图,在中, , , , BD是的角平分线,点P,点N分别是BD,AC边上的动点,点M在BC上,且 , 则的最小值为( ) A、3 B、 C、3.5 D、6. 如图,一根木棍斜靠在与地面垂直的墙上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
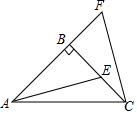
A、3 B、 C、3.5 D、6. 如图,一根木棍斜靠在与地面垂直的墙上,设木棍中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.在此滑动过程中,点P到点O的距离( )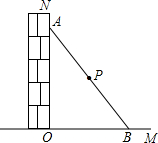 A、变小 B、不变 C、变大 D、无法判断7. 已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )A、1cm B、2cm C、4cm D、8cm8. 等腰三角形中, , 中点为D,过D作于 , , 则等于( )A、8cm B、7cm C、6cm D、4cm9. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交AC于点D,交BC于点E,交BA的延长线于点F,若 ,则BF的长为( )
A、变小 B、不变 C、变大 D、无法判断7. 已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )A、1cm B、2cm C、4cm D、8cm8. 等腰三角形中, , 中点为D,过D作于 , , 则等于( )A、8cm B、7cm C、6cm D、4cm9. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交AC于点D,交BC于点E,交BA的延长线于点F,若 ,则BF的长为( )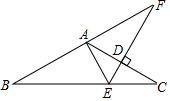 A、 B、3 C、 D、10. 若直角三角形一锐角为30° ,则它的三边之比可能是( )A、1:2:3 B、1:2: C、1 : : D、1:1 :
A、 B、3 C、 D、10. 若直角三角形一锐角为30° ,则它的三边之比可能是( )A、1:2:3 B、1:2: C、1 : : D、1:1 :二、填空题
-
11. 在 中, , , ,则 .12. 判别两个直角三角形全等的方法是.13. 在△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于D,AB=a,则DB等于.14. 如图,已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=2,则OM的长是.
 15. 如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=4,若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是.
15. 如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=4,若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是.
三、解答题
-
16. 已知:如图,点在线段上, , , , , 求证:.
 17. 如图,在 中, , ,线段 的垂直平分线 交 于 ,求证: .
17. 如图,在 中, , ,线段 的垂直平分线 交 于 ,求证: . 18. 如图, 是 的角平分线, , , .求证: .
18. 如图, 是 的角平分线, , , .求证: .