浙江省温州市乐清市2022年初中毕业升学考试适应性测试（一模）数学试卷

试卷更新日期：2022-06-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算： $(- 3) \times 5$ 的结果是（）

A、15 B、2 C、-2 D、-15

查看试题解析
2. 美国约翰斯·霍普金斯大学发布的统计数据显示，截至北京时间2022年2月15日23时59分，全球新冠肺炎确诊病例超过413 000 000例，其中死亡病例达到5 827 947例.数据413 000 000用科学记数法表示（）.

A、 $413 \times 1 0^{6}$ B、 $41.3 \times 1 0^{7}$ C、 $4.13 \times 1 0^{8}$ D、 $0.413 \times 1 0^{9}$

查看试题解析
3. 如图所示的几何体是由四个立方体组成的，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 某校安排三辆车，组织九年级学生团员去敬老院参加学雷锋活动，其中小王与小菲都可以从这三辆车中任选一辆搭乘，则小王与小菲同车的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{9}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析

5. 甲、乙、丙、丁四位射击运动员参加射击训练，获得如下数据：

	甲	乙	丙	丁
平均数（环）	9	9	8	8
方差（环²）	1.2	0.9	1.3	0.95

根据以上数据，哪位射击运动员射击成绩最好（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 若关于x的方程 $x^{2} - m x + 4 = 0$ 有实数根，则m的值可以是（）.

A、1 B、2 C、3 D、4

查看试题解析
7. 已知一个扇形的圆心角是150°，半径是3，则该扇形的弧长为（）

A、 $\frac{5}{2} π$ B、 $\frac{5}{4} π$ C、 $\frac{15}{2} π$ D、 $\frac{15}{4} π$

查看试题解析
8. 如图，一只正方体箱子沿着斜面CG向上运动， $∠ C = α$ ，箱高 $A B = 1$ 米，当 $B C = 2$ 米时，点A离地面CE的距离是（）米.

A、 $\frac{1}{c o s α} + \frac{2}{s i n α}$ B、 $\frac{1}{c o s α} + \frac{1}{2 s i n α}$ C、 $c o s α + 2 s i n α$ D、 $2 c o s α + s i n α$

查看试题解析
9. 如图，在平面直角坐标系中，点 $B$ 是抛物线 $y = a {(x - 1)}^{2} + 4$ 的图象的顶点，点 $A$ ， $C$ 的坐标分别为 $(0 ， 3)$ ， $(1 ， 0)$ ，将 $△ A B C$ 沿 $y$ 轴向下平移使点 $A$ 平移到点 $O$ ，再绕点 $O$ 逆时针旋转 $90 °$ ，若此时点 $B$ ， $C$ 的对应点 $B^{'}$ ， $C^{'}$ 恰好落在抛物线上，则 $a$ 的值为（）

A、 $- \frac{3}{4}$ B、－1 C、 $- \frac{4}{3}$ D、－2

查看试题解析
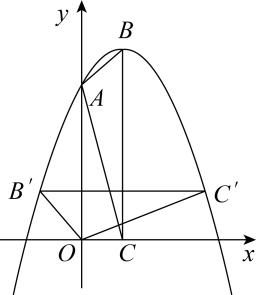10. 等积变换法是证明勾股定理的常用方法之一.如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以AB为边向下做正方形ADEB，CN平分 $∠ A C B$ 分别交AB，DE于M，N，过点A，B分别作 $A G ∥ B C$ ， $B F ∥ A C$ ，交CN于点G，F，连接DG，利用此图形可以证明勾股定理，记 $△ A M G$ ， $△ D G N$ 的面积分别为 $S_{1}$ ， $S_{2}$ ，若 $S_{1} + S_{2} = 7$ ， $F G = 2 \sqrt{2}$ ，则AB的长为（）

A、 $2 \sqrt{6}$ B、5 C、 $\sqrt{26}$ D、 $\sqrt{34}$

查看试题解析

二、填空题

11. 分解因式： $3 x^{2} - 12 =$ ．

查看试题解析
12. 不等式组： ${\begin{array}{l} 3 x + 2 > x \\ \frac{1}{3} x \leq 2 \end{array}$ 的解集为.

查看试题解析
13. 为了解某校1 000名学生对禁毒知识的掌握情况，随机抽取50名学生参加问卷测试，成绩进行整理得到频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，则该校成绩为80分及以上的学生约有人.

查看试题解析
14. 如图， $△ A B C$ 内接于⊙O， $∠ B A C = 25 °$ ， $△ A B C$ 外角 $∠ A B E$ 的平分线交⊙O于点D，若 $B C = B D$ ，则 $∠ C$ 的度数为.

查看试题解析
15. 如图，点A，B在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上， $A C ⊥ x$ 轴于点C， $B D ⊥ y$ 轴于点D，连接OA，AB，若 $O C = 3 B D = 6$ ， $O A = A B$ ，则k的值为.

查看试题解析
16. 如图1为某智能洗拖一体扫地机，它正常工作及待机充电时的示意图如图2所示，四边形ABCD为它的手柄，OE为支撑杆，OM为拖把支架，且点O始终在AB的延长线上，当待机时， $B C ∥ O M$ ，已知 $A B = 18 c m$ ， $B C = 15 c m$ ， $∠ A B C = ∠ C = 90 °$ ， $A D + C D = 27 c m$ ，则 $C D =$ cm；OE绕点O逆时针旋转一定角度，机器开始工作，当 $D^{'}$ ， $C^{'}$ ， M在同一直线上时，点A，B分别绕O点旋转到点 $A^{'}$ ， $B^{'}$ ，且高度分别下降了21.6cm和18cm，则此时点 $D^{'}$ 到OM距离为cm.

查看试题解析

三、解答题

17.

(1)、计算： $| - 3 | - \sqrt{4} + {(\sqrt{3} + 1)}^{0} + (- 5)$ ；

(2)、化简： $\frac{2 x - 2}{x^{2} - 1} + \frac{2 x}{x + 1}$ ；

查看试题解析
18. 如图，A，E，F，B在同一条直线上， $C E ⊥ A B$ ， $D F ⊥ A B$ ，垂足分别为E，F， $A E = B F$ ， $∠ A = ∠ B$ .

(1)、求证： $△ A D F ≅ △ B C E$ .

(2)、当 $B C ⊥ A D$ ， $A E = \sqrt{2}$ ， $O A = 3$ 时，求OD的长.

查看试题解析
19. 2021年下半年，乐清市进行了学生健康午休工程，促进学生健康成长.小明随机选取乐清市A，B两所学校各200名学生进行午休工程的满意度调查，满意度分值为1分、2分、3分、4分、5分五个等级，现将两所学校的满意度调查数据整理并分别绘制成统计图如图所示.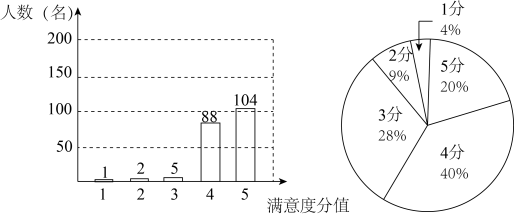

(1)、求出A，B两所学校的满意度分值的平均数、中位数、众数.

(2)、根据（1）的结果，选择适当的统计量，简略说明哪所学校的学生对健康午休工程的满意度更好.

查看试题解析
20. 如图， $4 \times 5$ 的方格纸ABCD是由边长为1的小正方形组成的，请按要求画格点线段与格点四边形，端点或顶点均在格点上，且不与点A，B，C，D重合.

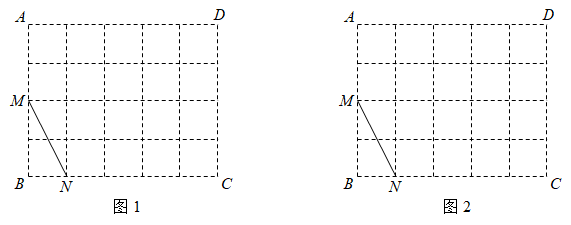(1)、在图1中画一条格点线段MQ，使MQ的长度为 $\sqrt{2} M N$ .

(2)、在图2中画一个格点四边形MNPQ，使点P，Q分别落在边CD，DA上，且四边形MNPQ的面积为10.

查看试题解析
21. 已知抛物线 $y = a x^{2} - 4 a x + 3 (a \neq 0)$ 的图象经过点 $A (- 2 ， 0)$ ，过点A作直线l交抛物线于点 $B (4 ， m)$ .

(1)、求抛物线的函数表达式和顶点坐标.

(2)、将抛物线向下平移 $n (n > 0)$ 个单位，使顶点落在直线l上，求m，n的值.

查看试题解析
22. 如图， $△ A B C$ 内接于⊙O， $A B = A C = 10$ ， $B C = 12$ ，点E为 $\overset{⌢}{A C}$ 上一点，点F为 $\overset{⌢}{C E}$ 的中点，连结BF并延长与AE交于点G，连结AF，CF.

(1)、求证： $∠ A F C = ∠ A F G$ .

(2)、当BG经过圆心O时，求FG的长.

查看试题解析
23. 2022年北京冬奥会吉祥物“冰墩墩”万众瞩目，硅胶是生产“冰墩墩”外壳的主要原材料.某硅胶制品有限公司的两个车间负责生产“冰墩墩”硅胶外壳，已知每天生产的硅胶外壳数量甲车间是乙车间的两倍，甲车间生产8000个所用的时间比乙车间生产2000个所用的时间多一天.

(1)、求出甲、乙两车间每天生产硅胶外壳个数.

(2)、现有如下表所示的A，B两种型号硅胶外壳，该公司现有378千克的原材料用于生产外壳，并恰好全部用完.
型号
所需原材料
冰墩墩单价
A
99克
198元
B
90克
192元
①若生产的A，B两种型号的外壳共4000个，求出A，B两种型号的外壳个数.
②若生产的A，B两种型号的外壳若干个用于销售，且A型号的数量大于B型号的数量，则A型号外壳为多少个时，冰墩墩的销售金额最大.求出最大销售金额.

查看试题解析
24. 如图1，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ， BD平分 $△ A B C$ 的外角 $∠ A B M$ ， $A D ⊥ B D$ 于点D，过B点作 $B E ∥ A C$ 交AD于点E.点P在线段AB上（不与端点A点重合），点Q在射线BC上，且 $C Q = 2 A P = 2 t$ ，连接 PQ，作P点关于直线BE的对称点N，连接PN，NQ.

(1)、求证： $∠ B A D = ∠ D B E$ .

(2)、当Q在线段BC上时，PN与AD交于点H，若 $A H = E H$ ，求HP的长.

(3)、①当 $△ P N Q$ 的一边与 $△ A B D$ 的AD或BD边平行时，求所有满足条件的t的值.
②当点D在 $△ P N Q$ 内部时，请直接写出满足条件的t的取值范围.

查看试题解析

型号	所需原材料	冰墩墩单价
A	99克	198元
B	90克	192元