浙江省绍兴市嵊州市2022年初中毕业生学业评价调测数学试卷
试卷更新日期:2022-06-07 类型:中考模拟
一、单选题
-
1. 2022的相反数是( )A、2022 B、 C、﹣2022 D、2. 2022年1月8日,杭绍台高铁正式通车,全线设8个车站,设计时速350千米,全长266900米,数字266900用科学记数法可表示为( )A、2.669×106 B、0.2669×107 C、2.669× 105 D、26.69×1043. 如图的几何体由五个相同的小正方体搭成,它的主视图是( )
 A、
A、 B、
B、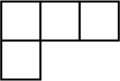 C、
C、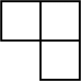 D、
D、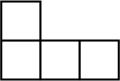 4. 下列运算正确的是( )A、(xy2)2=xy4 B、x2·x4=x8 C、x6÷x2=x3 D、2x2+3x2= 5x25. 一个不透明的袋中装有 7个只有颜色,不同的球,其中3个红球,2个蓝球和2个黄球.从袋中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、6. 如图1,校运动会上,初一的同学们进行了投实心球比赛. 我们发现, 实心球在空中飞行的轨迹可以近似看作是抛物线. 如图7-2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是 , 则该同学此次投掷实心球的成绩是( )
4. 下列运算正确的是( )A、(xy2)2=xy4 B、x2·x4=x8 C、x6÷x2=x3 D、2x2+3x2= 5x25. 一个不透明的袋中装有 7个只有颜色,不同的球,其中3个红球,2个蓝球和2个黄球.从袋中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、6. 如图1,校运动会上,初一的同学们进行了投实心球比赛. 我们发现, 实心球在空中飞行的轨迹可以近似看作是抛物线. 如图7-2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是 , 则该同学此次投掷实心球的成绩是( )
 A、2m B、6m C、8 m D、10 m7. 如图,在平面直角坐标系xOy中,△ABC与△ODE是位似图形,则它们的位似中心的坐标是( )
A、2m B、6m C、8 m D、10 m7. 如图,在平面直角坐标系xOy中,△ABC与△ODE是位似图形,则它们的位似中心的坐标是( ) A、(4,4) B、(4,3) C、(4,2) D、(3,4)8. 如图,是的内接三角形, , 是直径, , 则的长为( )
A、(4,4) B、(4,3) C、(4,2) D、(3,4)8. 如图,是的内接三角形, , 是直径, , 则的长为( ) A、4 B、 C、 D、9. 如图,在□ABCD中, E为BC边上的点,满足BE= 5CE,若四边形AEDF为正方形,则tanB的值为( )
A、4 B、 C、 D、9. 如图,在□ABCD中, E为BC边上的点,满足BE= 5CE,若四边形AEDF为正方形,则tanB的值为( ) A、1 B、 C、2 D、10. 有六名同学需要在某天内每人交一份作北给老师,每名同学交作业时将作业放在作业堆的最上面,老师一有空就从最上面拿一份作业来批改.按交作业的先后顺序将六份作业依次编号为①、②、③、④、⑤、⑥.已知当天中午老师已经批改完两份作业,第二份作业编号为④.则老师下午作业批改的顺序不可能为( )A、③⑥⑤① B、②⑥①⑤ C、③⑤⑥② D、⑤③①⑥
A、1 B、 C、2 D、10. 有六名同学需要在某天内每人交一份作北给老师,每名同学交作业时将作业放在作业堆的最上面,老师一有空就从最上面拿一份作业来批改.按交作业的先后顺序将六份作业依次编号为①、②、③、④、⑤、⑥.已知当天中午老师已经批改完两份作业,第二份作业编号为④.则老师下午作业批改的顺序不可能为( )A、③⑥⑤① B、②⑥①⑤ C、③⑤⑥② D、⑤③①⑥二、填空题
-
11. 分解因式:x2-6x+9=.12. 分式方程 = 的解为 .13. 已知扇形的圆心角为30°,面积为 ,则该扇形的半径为 .14. 如图,在△ABC中,AB=AC,∠A=36°,分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,再以点B为圆心,BC长为半径作弧,交直线MN于点E,则∠BEC的度数为.
 15. 点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴,y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3.若OF=FG= GA,S1+S3=10,则S2的值为.
15. 点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴,y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3.若OF=FG= GA,S1+S3=10,则S2的值为. 16. 如图,在△ABC中,AB= AC=2 , ∠BAC=120°,D为直线BC上一点,连结AD,把线段AD绕点A按逆时针旋转60°得到线段AE,H是线段AE的中点,G是线段BC的中点,连结DE,GH,若= , 则GH的长为.
16. 如图,在△ABC中,AB= AC=2 , ∠BAC=120°,D为直线BC上一点,连结AD,把线段AD绕点A按逆时针旋转60°得到线段AE,H是线段AE的中点,G是线段BC的中点,连结DE,GH,若= , 则GH的长为.
三、解答题
-
17.(1)、tan60-|-2|+(-1)0(2)、解不等式组:18. 为了解《关于全面加强新时代大中小学劳动教育的意见》的落实情况,某校从全体学生中随机抽取部分学生,调查他们平均每周劳动时间t(单位: h),按劳动时间分为四组:A组“t <5”,B组“5≤t<7”,C组“7<t<9”,D组“t>9”.将收集的数据整理后,绘制成如下两幅不完整的统计图.
某校部分学生平均每周劳动时间条形统计图

某校部分学生平均每周劳动时间扇形统计图

根据以上信息,解答下列问题:
(1)、本次接受问卷调查的学生有多少人?并求图2中C组所在扇形圆心角的度数;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请你估计该校平均每周劳动时间不少于7h的学生人数.19. 如图,在△ABC中, 点D,E,F分别在AB,BC,AC边上, , . (1)、求证:;(2)、若 , △EFC的面积为20, 求△ABC的面积.20. 某销售公司推销一种产品, 每月付给销售人员的工资有两种方案.
(1)、求证:;(2)、若 , △EFC的面积为20, 求△ABC的面积.20. 某销售公司推销一种产品, 每月付给销售人员的工资有两种方案.方案一:没有底薪,只付销售提成;
方案二:底薪加销售提成.
设x(件)是推销产品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.
 (1)、分别求y1 , y2关于x 的函数表达式;(2)、若该公司某销售人员1月份推销产品的数量没有超过70件,但其1月份的工资超过2000元.公司采用哪种方案给这名销售人员付1月份的工资?21. 已知,图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂可伸缩(),且起重臂可绕点在一定范围内转动,张角为(),转动点距离地面的高度为.
(1)、分别求y1 , y2关于x 的函数表达式;(2)、若该公司某销售人员1月份推销产品的数量没有超过70件,但其1月份的工资超过2000元.公司采用哪种方案给这名销售人员付1月份的工资?21. 已知,图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂可伸缩(),且起重臂可绕点在一定范围内转动,张角为(),转动点距离地面的高度为. (1)、当起重臂长度为 , 张角为120°时,求云梯消防车最高点距离地面的高度;(2)、某日,一居民家突发险情,该居民家距离地面的高度为 , 请问该消防车能否实施有效救援?(参考数据:)22. 已知抛物线y=ax2 +bx+ l经过点(1,-2), (-2,13).(1)、求a,b的值;(2)、若(5,y1),(n,y2)是抛物线上不同的两点,且y2=12-y1 , 求n的值;(3)、将此抛物线沿x轴平移m(m>0)个单位长度,当自变量x的值满足-1≤x≤3时,与其对应的函数值y的最小值为6,求m的值.23. 如图,在正方形ABCD中,E是CD边上一点(不与D点重合),F是CB延长线上一点,且DE=BF,连结AE,AF.
(1)、当起重臂长度为 , 张角为120°时,求云梯消防车最高点距离地面的高度;(2)、某日,一居民家突发险情,该居民家距离地面的高度为 , 请问该消防车能否实施有效救援?(参考数据:)22. 已知抛物线y=ax2 +bx+ l经过点(1,-2), (-2,13).(1)、求a,b的值;(2)、若(5,y1),(n,y2)是抛物线上不同的两点,且y2=12-y1 , 求n的值;(3)、将此抛物线沿x轴平移m(m>0)个单位长度,当自变量x的值满足-1≤x≤3时,与其对应的函数值y的最小值为6,求m的值.23. 如图,在正方形ABCD中,E是CD边上一点(不与D点重合),F是CB延长线上一点,且DE=BF,连结AE,AF. (1)、如图1,求证:△ADE≌△ABF .(2)、把△ADE沿AE所在直线折叠后得到△AGE,连结FG,BE.
(1)、如图1,求证:△ADE≌△ABF .(2)、把△ADE沿AE所在直线折叠后得到△AGE,连结FG,BE.①如图2,若CD=3,DE=1,求线段FG的长;
②如图3,若E是DC延长线上一点,延长GB交AE于点Q,连结DQ.若DE=2DC,请用等式表示线段BQ,DQ,FG之间的数量关系,并证明.
24. 在平面直角坐标系xOy中,已知点P(4,3),⊙O经过点P,过点P作x轴的平行线交⊙O于点E. (1)、如图1,求线段OP的长;(2)、点A为y轴正半轴上的一动点,点B和点A关于直线PE对称,连接PA,PB.直线PA,PB分别交⊙O于点C,D.直线CD交x轴于点F,交直线PE于点G.
(1)、如图1,求线段OP的长;(2)、点A为y轴正半轴上的一动点,点B和点A关于直线PE对称,连接PA,PB.直线PA,PB分别交⊙O于点C,D.直线CD交x轴于点F,交直线PE于点G.①点A运动到如图2位置,连接CE,DE.求证:∠DGP=ECP.
②在点A运动过程中,当DF=OP时,求点D的坐标.